Рассмотренные элементарные мыслительные операции в сочетании с правилами их введения и удаления тем не менее оставляют нерешенной основную проблему мышления: проблему построения самих умозаключений, т.е. процедуру организации структуры мыслительного процесса. Действительно, как выглядят хотя бы самые общие подходы к решению задач?
Рассмотрим пример, в котором мы имеем среди исходных данных набор фактов, включающих отдельные высказывания (простые или сложные): А, В, L, а также высказывания в виде импликаций: А→L, A→B, F→C, B→D, B→G, G→T, K→G, L→B, L→K. Для простоты будем считать, что единственным правилом вывода в этом примере будет правило отделения. Многократно применяя правило отделения, мы можем получить новое знание, например, в виде А→T Действительно, из А и А→В получаем В, затем из В и В→G получаем G, затем из G и G→T получаем Т. Формально в математической логике три шага данного вывода записываются как:
В такой записи над чертой записываются посылки, под чертой - следствия. При этом заметим, что в итоге мы построили умозаключение А→Т и одновременно получили цепочку рассуждения: А, A→B→G→T.
Заметим также, что данная цепочка не является единственно возможным путем для получения результата А→Т. Этот же вывод из имеющихся данных мы можем получить, построив и другие цепи доказательств.
71
Например, цепь № 2: из А, А→L получаем L, затем из L, L →В получаем В, далее логический вывод идет так же, как в предыдущем случае. Цепь № 3 напишем в сокращенном виде: А, А→L→К→G→T.
Данный пример удобно представить не только в аналитическом, но и в образном виде, как часть графа или семантической сети (рис. 28). Такого рода представления служат целям структурирования информации. В каждом узле сети собирается вся информация по некоторому объекту или по некоторой ситуации. Эта информация представляется в виде наборов характеристик или атрибутов объекта, а также в виде ссылок, указывающих связи между узлами (объектами).
В общем виде для обозначения структурированной системы данных, касающихся некоторого объекта или "ядра" знаний, касающихся данной области, используется термин фрейм (от англ, frame - каркас, рамка). При этом понятие фрейма является достаточно широким: структура фрейма может быть разной для разных областей знаний и рассуждений. Причем данное условие не является причудой или экзотикой - оно отражает принципиальный факт различия природы разных областей знаний. (Едва ли вызовет удивление, что организация блока знаний в физике и в истории права имеет различное строение.)
Заметим, что в нашем примере в процессе логического дедуктивного вывода мы не явным образом считали, что все исходные высказывания имеют в процессе решения данной задачи одинаковые приоритеты. Вследствие этого все три цепочки логического вывода (все три умозаключения) имели одинаковую вероятность построения. Более того, на основе имеющихся фактов мы с равной вероятностью могли начинать строить вывод, исходя не из факта A, а из фактов В, В→D или каких-то других. В результате предположения равной вероятности взаимных связей между фактами в ходе построения логического вывода возникает огромный перебор вариантов, причем с ростом длины вывода время перебора растет лавинообразно. Для того чтобы уменьшить эту опасность (а полностью избежать ее невозможно), необходимо использовать системы приоритетов, указывающие разные вероятности связей между разными фактами, или, другими словами, разные вероятности ссылок (рис. 28).
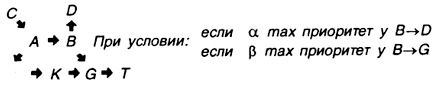Рис. 28. Участок семантической сети в хорошо структурированной области знаний
72
При этом приоритеты ссылок, естественно, зависят от многих параметров, описывающих контекст ситуации. К числу таких параметров относятся различные условия, которые должны быть проверены или как-то определены перед принятием решения. В примере на рис. 28 типичной записью в узле В может быть: "При условии максимальный приоритет имеется у ссылки В→D, при условии максимальный приоритет у ссылки В→G". В качестве условия могут выступать различные атрибуты объекта, например, такие, как значения физических параметров, временные значения, полученная к текущему моменту информация о состоянии других узлов (объектов) и т.д.
73
