Глава 9. ОБЩЕЕ ЭКОНОМИЧЕСКОЕ
РАВНОВЕСИЕ И ОБЩЕСТВЕННОЕ
БЛАГОСОСТОЯНИЕ
В предыдущих темах мы рассматривали процесс установления рыночного равновесия на моделях частичного равновесия, то есть равновесия, складывающегося на отдельном рынке. При этом не учитывалось, как изменение цены одного блага влияет на цены других благ, и игнорировался возникающий в этом случае эффект обратных связей. В действительности все цены находятся в тесном взаимодействии.
В предыдущей главе было показано, что цена фактора производства определяется ценой производимого им блага, а через затраты производства цена фактора оказывает обратное воздействие на цену блага. Поскольку одни и те же факторы применяются при производстве различных благ, то цены последних оказываются взаимосвязанными.
Предметом исследования данной темы является общее равновесие или равновесие, возникающее в результате взаимодействия всех рынков, когда изменение спроса или предложения на одном рынке влияет на равновесные цены и объемы продаж на всех рынках.
Равновесие называется общим, если система взаимосвязанных цен обеспечивает одновременное равенство спроса и предложения на всех рынках.
Естественно, что модели общего экономического равновесия по сравнению с моделями частичного равновесия являются более сложными. Мы рассмотрим наиболее простую модель общего экономического равновесия - модель Л. Вальраса, изложенную им в работе "Элементы чистой политической экономии" (1889г.).
Рассматривается экономическая система, в которой производится п товаров с помощью m видов ресурсов или факторов производства. Обозначим через ri количество i-го ресурса, а через хj - количество j-гo товара. Техническая характеристика производственных возможностей дается при помощи mn фиксированных коэффициентов затрат аij , показывающих расход i-го ресурса для
182
производства единицы j-гo товара. Предполагая равенство спроса и предложения по каждому виду ресурсов, получаем m уравнений:
a11x1 + a12x2 + … + a1nxn = r1,
a21x1 + a22x2 + … + a2nxn = r2,
(9.1)
…
am1x1 + am2x2 + … + amnxn = rn.
Введем в качестве m+n переменных цены товаров (Р1, Р2, ... , Рn) и цены факторов производства (V1, V2, ... , Vm).
Уравнения рыночного спроса на товары представляются в следующем виде:
X1 = F1(P1, P2, … , Pn; V1, V2, … ,Vm),
X2 = F2(P1, P2, … , Pn; V1, V2, … ,Vm),
(9.2)
…
Xn = Fn(P1, P2, … , Pn; V1, V2, … ,Vm).
Цены факторов производства вводятся в функции спроса для того, чтобы учесть изменения спроса на товары в связи с изменением уровня и распределения доходов. Удвоение всех цен на товары и факторы производства не меняет положения участников рыночного обмена и, следовательно, не влияет на индивидуальный и совокупный спрос.
Поскольку рассматриваются условия конкурентного равновесия применительно к длительному периоду, сохраняется классическая предпосылка о равенстве цены товара издержкам его производства:
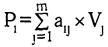
А так как промежуточные продукты в модели отсутствуют, полные издержки производства единицы товара сводятся к оплате производственных факторов в соответствии с их ценами. Это условие выражается следующими n условиями:
A11V1 + a21V2 + … +am1Vm = P1,
A12V1 + a22V2 + … +am2Vm = P2,
(9.3)
…
A1nV1 + a2nV2 + … +amnVm = Pn.
Для завершения системы следует определить условия предложения факторов производства. Предполагается, что оно зависит от рыночных цен на эти факторы, а также от цен на конечные товары. Последняя группа уравнений представляется в следующем виде:
183
r1 = G1(P1, P2, … , Pn; V1, V2, …, Vm),
r2 = G2(P1, P2, … , Pn; V1, V2, …, Vm),
(9.4)
…
rm = Gm(P1, P2, … , Pn; V1, V2, …, Vm),
Подобно функциям спроса (уравнение 9.2), функции предложения являются однородными нулевой степени. Более того, сумма расходов каждого участника обмена ограничена суммой его доходов от факторов производства и это условие справедливо для системы в целом. Стало быть, функции совокупного рыночного спроса и предложения не являются независимыми, они удовлетворяют тождеству:
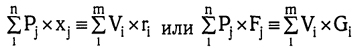
При условии постоянства технологических коэффициентов это отношение вытекает из (9.1) и (9.3). Умножив первое уравнение из (9.1) на V1, второе - на V2 и так далее и суммируя эти m уравнений, получим в левой части
∑aij × Vi × xj,
а в правой
∑Vi × ri.
Умножив первое уравнение из (9.3) на х1, второе - на х2 и так далее и суммируя эти n уравнений, получим в левой части
∑aij ×Vi × xj,
а в правой -
∑pj × xj.
Таким образом,
∑pj × xj ≡ ∑ Vi × ri.
Решение модели Вальраса определяет одновременно равновесные цены и объемы производства по всем отраслям.
Основное равенство, так называемый закон Вальраса, утверждает, что общая величина спроса должна быть при соответствующей системе цен равна общей величине предложения. На этой основе доказывается, что необходимое число уравнений в системе не равно общему числу рассматриваемых товаров и ресурсов, как можно было бы предположить, а на единицу меньше: последнее уравнение обязательно вытекает из совокупности остальных.
Конечно, модель Л. Вальраса несколько идеализировала действительность. В ней предусматривалось, что потребители знают свои функции спроса и предложения, технические коэффициенты и многие другие данные. Модель общего равновесия исходит из совершенной конкуренции, предполагающей идеальную
184
мобильность всех ресурсов, полную информированность участников, абсолютизирует состояние равновесия, тогда как в реальной действительности гораздо чаще встречаются диспропорции и дисбалансы.
Исследование модели Л. Вальраса, сводится, таким образом, к решению трех основных вопросов:
- 1) существует ли решение данной системы уравнений, то есть возможна ли система цен, количеств товаров и ресурсов, совместных друг с другом;
- 2) единственно ли это решение в том смысле, что для каждой переменной существует только одно значение, совместное с общим решением;
- 3) стабильна ли система, способна ли она возвращаться к равновесию при его нарушении.
Ответы на эти вопросы возможны при введении ряда экономически приемлемых ограничений.
185
