Теория производства исходит из того, что для выпуска продукции используются два вида ресурсов: L и К, цены которых (соответственно w и r) заданы. В этом случае общие затраты (ТС) предприятия можно представить тождеством:
TC ≡ wL+rK.
(5.1)
Затраты, следовательно, зависят от цен ресурсов и объема выпуска, а он, в свою очередь, зависит от количества используемых ресурсов L и К. Зависимость между ценами ресурсов, их количеством, объемом выпуска и общими затратами можно представить с помощью функции затрат.
Функция затрат характеризует минимальную сумму затрат как функцию объема выпуска и цен ресурсов. Иначе, функция затрат характеризует общий уровень затрат на выпуск заданного объема продукции при использовании оптимальной комбинации ресурсов L и К. Как было показано в гл. 4, эта оптимальная комбинация определяется координатами точки касания изокванты, соответствующей данному выпуску, и изокосты. Следовательно, тождество (5.1) можно в общем случае представить в виде функции:
TC(Q) = f [Q(L, К), w, r].
(5.2)
Если предположить, что цены на ресурсы w и r остаются неизменными, то функцию затрат можно представить графически в виде кривой затрат (рис. 5.1). При этом следует различать долгосрочные затраты, или затраты в длительном периоде (LTC; long-run total cost - англ.), и краткосрочные затраты, или затраты в коротком периоде (STC; short-run total cost - англ.).
В длительном периоде, как известно, все ресурсы являются переменными, и кривая LTC может быть получена на основе множеств изоквант, каждая из которых представляет некоторую производственную функцию, и изокост, характеризующих определенное соотношение цен на ресурсы (рис. 5.1, а).
Главным фактором, который определяет конфигурацию LTC, является характер отдачи от масштаба. При этом кривые затрат всегда исходят из начала координат, поскольку в длительном периоде нет постоянных затрат.
При постоянной отдаче от масштаба кривая LTC имеет вид прямой линии или луча (рис. 5.1, б). Это означает, что общие затраты увеличиваются в той же
86
пропорции, в какой растет объем выпуска, который сам возрастает пропорционально увеличению количества применяемых ресурсов.
При возрастающей отдаче от масштаба объем выпуска будет опережать рост количества применяемых ресурсов, то есть затраты на выпуск 2Q1 будут меньше, чем удвоенные затраты на выпуск Q1 (рис. 5.1, в). Поэтому кривая LTC будет выпукла вверх (рис. 5.1, г). Это свидетельствует о том, что общие затраты с ростом объема выпуска возрастают, но возрастают все медленнее.
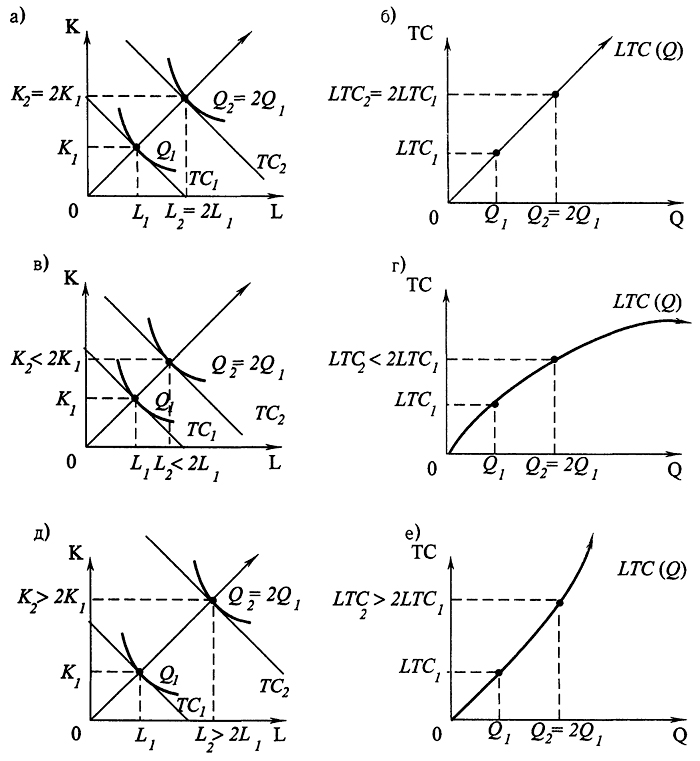 Рис. 5.1.
Рис. 5.1. Изокванты и кривые долгосрочных затрат LTC при разном характере отдачи от масштаба: а, б - при постоянной отдаче; в, г - при возрастающей отдаче; д, е - при убывающей отдаче
87
При убывающей отдаче от масштаба затраты будут расти в большей мере, чем выпуск, то есть для удвоения объема выпуска потребуется более чем вдвое увеличить количество применяемых ресурсов (рис. 5.1 ,д). Поэтому кривая LTC будет вогнута или выпукла вниз (рис. 5.1, е).
Как отмечалось в гл. 4, на многих предприятиях возрастающая отдача от масштаба при достижении некоторого объема выпуска сменяется на убывающую. В этой ситуации кривая LTC до определенного уровня производства будет выпукла вверх, а затем - вниз (рис. 5.2, а).
Для анализа кривой LTC следует ввести понятия долгосрочных предельных затрат (LMC, long-run marginal cost - англ.) и долгосрочных средних затрат (LATC, long-run average total cost - англ.).
Предельные затраты вообще (МС) определяются как изменение общих затрат при увеличении выпуска продукции на единицу:
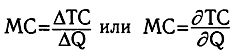 (5.3)
(5.3)
Это определение применимо для анализа затрат как в длительном, так и коротком периоде. Различие же между ними заключается в том, что долгосрочные предельные затраты (LMC) определяются, когда все производственные ресурсы будут переменными, а краткосрочные предельные затраты (SMC) - когда часть ресурсов будет переменной, а часть - постоянной.
Графически предельные затраты определяются тангенсом угла наклона касательной к кривой общих затрат в любой точке, соответствующей какому-либо объему выпуска. На рис. 5.2, а видно, что угол наклона касательной КК к кривой LTC в точке перегиба А меньше угла наклона в любой другой точке LTC. Поэтому минимум LMC достигается при объеме выпуска Q1 (рис. 5.2, б). Вплоть до достижения объема выпуска Q1 предельные затраты будут убывать, а затем начнут возрастать.
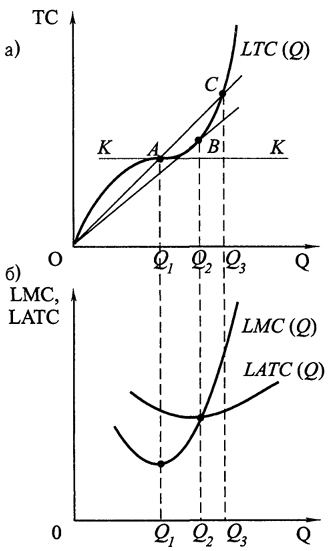 Рис. 5.2.
Рис. 5.2. Затраты в длительном периоде
Средние или удельные (unit cost - англ.) затраты (АТС) определяются как отношение общих затрат к объему выпуска:
ATC = TC / Q.
(5.4)
При этом долгосрочные средние затраты (LATC) рассчитываются при условии, что все производственные ресурсы
88
являются переменными, а краткосрочные средние затраты (SATC) - при условии, что часть ресурсов является переменной, а другая часть - постоянной.
Графически средние затраты определяются тангенсом угла наклона луча, исходящего из начала координат, к кривой общих затрат в любой точке, соответствующей какому-либо объему выпуска. На рис. 5.2, а луч ОВ имеет наклон меньше, чем луч, проведенный из начала координат, к кривой общих затрат в любой другой точке на кривой LTC. Поэтому минимум LATC достигается при объеме выпуска Q2 (рис. 5.2, б). При этом объеме выпуска LATC = BQ2 / OQ2.
На рис. 5.2 видно, что при объеме выпуска Q2 имеет место равенство долгосрочных средних затрат и долгосрочных предельных затрат, то есть LATC = LMC. Действительно, луч ОВ, наклон которого определяет LATC, одновременно является и касательной к кривой общих затрат в точке В, наклон которой определяет LMC.
Следовательно, можно выделить следующий важный принцип: средние затраты будут минимальными при таком объеме выпуска, при котором они равны предельным. При этом кривая LMC должна пересекать кривую LATC снизу вверх направо. Из рис. 5.2, б видно также, что при объеме выпуска меньшем, чем Q2, LATC больше LMC.
В коротком периоде, в отличие от длительного, предприятие не может изменить объем выпуска за счет изменения количества всех производственных ресурсов. Поэтому оно двигается не вдоль луча, исходящего из начала координат (линии роста), а вдоль линии, параллельной оси переменного ресурса. Следовательно, кривая краткосрочных затрат не совпадает с кривой долгосрочных затрат, проходя выше кривой LTC везде, кроме точки взаимного касания (рис. 5.3).
На рис. 5.3, а представлено семейство изоквант Q1-Q3. Если бы предприятие могло изменять количество ресурсов L и К, то их оптимальные комбинации располагались бы вдоль линии роста. Соответствующая кривая LTC приведена на рис. 5.3, б.
Допустим, что предприятие находится в точке F на линии роста (рис. 5.3, а), выпуская Q2 единиц продукции при затратах ТС2. Если предприятие захочет сократить выпуск до Q1 то оно не сможет сделать это, двигаясь вдоль линии
 Рис. 5.3.
Рис. 5.3. Изокванты и кривые долгосрочных (LTC) и краткосрочных (STC) затрат
89
роста в точку Е и соответственно снижая сумму затрат до ТС1. В коротком периоде ему придется двигаться вдоль линии постоянного ресурса КК к точке Е'. При этом точка Е' не является точкой касания изокванты Q1, и изокосты TC1, поэтому она представляет более высокий уровень затрат, чем точка Е. Это вытекает из того, что изокоста ТС1', проходящая через точку Е', лежит выше изокосты, проходящей через точку Е (TC1). Значит, общие затраты в точке Е' выше, чем TC1 (рис. 5.3, б). Следовательно, в коротком периоде при выпуске меньшем, чем Q2, STC>LTC. Даже в случае прекращения выпуска, то есть при Q = О, предприятию не удастся уменьшить количество постоянного ресурса и, таким образом, оно вынуждено будет нести определенные затраты. Эти затраты называются постоянными. На рис. 5.3, б постоянные затраты равны С0.
Теперь предположим, что предприятие хочет увеличить выпуск до Q3. Однако в коротком периоде точка G для него недостижима, так как количество постоянного ресурса ограничено. Поэтому для достижения объема выпуска Q3 предприятию придется перейти в точку G'. При этом, как и в положении Е', STC будут выше LTC. Только при объеме выпуска Q2 долгосрочные и краткосрочные затраты равны, то есть LTC(Q2) = STC(Q2). Это связано с тем, что при объеме выпуска Q2 линия роста ОА пересекается линией постоянного ресурса, параллельной оси переменного ресурса (точка F на рис. 5.3, а). Именно при выпуске Q2 фиксированное количество ресурса К будет оптимальным. При любом другом выпуске кривая STC пройдет выше кривой LTC, так как невозможность изменить количество постоянного ресурса в коротком периоде не позволяет достичь того минимума затрат, который возможен в длительном периоде.
Различия в количествах постоянного ресурса К приводят и к различным кривым краткосрочных затрат. Увеличение количества постоянного ресурса К можно представить как сдвиг линии КК вверх (рис. 5.3, а). При этом линия КК будет пересекать луч ОА выше и правее точки F, то есть при большем объеме выпуска. Новая кривая краткосрочных затрат в результате будет касаться кривой LTC также при большем выпуске.
На рис. 5.4 приведены кривые краткосрочных затрат STC1- STC3 при разных объемах постоянного ресурса. Следовательно, кривую долгосрочных затрат LTC можно представить как огибающую для бесконечного числа кривых краткосрочных затрат.
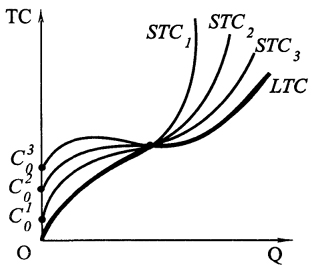 Рис. 5.4.
Рис. 5.4. Кривая долгосрочных затрат LTC как огибающая кривых краткосрочных затрат
90
