15.2. Модель эволюции кооперации

Рассмотрим модель "Дилеммы заключенного" в динамике, предполагая, что социальное взаимодействие носит не разовый характер, а может неоднократно повторяться в будущем. В так называемой итеративной дилемме заключенного предполагается, что стороны, принимая решения, учитывают опыт прошлых взаимодействий и прогнозируют возможное поведение партнеров в будущем. При этом таблица выигрышей остается неизменной.

Исследованию этой модели посвящена книга Р. Аксельрода "Эволюция кооперации" [5], центральной проблемой которой является выявление и анализ механизмов, формирующих кооперативное поведение среди эгоистических индивидов без какого-либо принуждения или указаний свыше. Ясно, что кооперативные механизмы возникают только при определенных условиях. Примерами

276

являются взаимодействие государств на международной арене, компромиссы, достигаемые сторонниками противоборствующих партий в парламенте, соблюдение неписаных правил поведения в бизнесе и т.д.

Анализ дилеммы заключенного, проведенный в § 15.1, показал, что следование принципам индивидуальной рациональности заставляет "разумных" игроков отказываться от кооперации, выбирая вариант (D; D). Что же меняется, если с данным партнером социальные взаимодействия могут повторяться? Допустим, стороны знают, что игра повторится ровно десять раз. Казалось бы, целесообразно перейти к взаимному сотрудничеству (вариант С; С), приносящему существенно больший выигрыш. Однако игрок А считает иначе. Он думает, что партнер В будет все время выбирать кооперацию и решает попытаться выиграть, обманывая в последней, десятой игре. Также рассуждает игрок В. Понимая, что оба в последней игре выберут альтернативу D, игроки, обдумывая свою стратегию в девятой игре, приходят к тому же выводу и т.д. Таким образом, рациональной вновь оказывается стратегия D - отказ от сотрудничества. Каждому из игроков эта стратегия принесет по 10 руб., тогда как сотрудничество дало бы каждому по 30 руб. Противоречие между индивидуальной и коллективной рациональностью сохранилось.

Ситуация коренным образом меняется, если игроки не знают, когда закончится игра. Какой же стратегии целесообразно придерживаться в данном случае?

Дать теоретически обоснованный ответ на этот вопрос довольно трудно, и Аксельрод предложил своим коллегам выявить лучшую стратегию в честном спортивном соревновании. Ведущие специалисты, занимающиеся этой проблематикой, - психологи, экономисты, математики, социологи - прислали Аксельроду свои варианты стратегии данной игры, реализованные в виде компьютерных программ. В турнире участвовали 63 программы. Каждая пара программ проводила друг с другом серии по 200 игр. Точное число игр авторам программ не сообщалось. Присланные программы содержали как простые стратегии, так и весьма изощренные, использующие методы прогнозирования и искусственного интеллекта. Победителем объявлялась программа, набравшая в турнире больше всего очков. Удивительно, что чемпионом оказалась самая короткая программа, присланная А. Рапопортом, реализующая самую простую стратегию "Зуб за зуб" (TIT FOR TAT, сокращенно TFT).

277

Стратегия TFT на первом ходу выбирает кооперацию, а затем просто повторяет ходы партнера. Если он в предыдущей игре выбрал обман (D), то TFT также выбирает обман. Если партнер в предыдущей игре предпочел кооперацию (С), то TFT также считает необходимым его поддержать.

Стратегия "Зуб за зуб" была хорошо известна еще в древние времена. Ей соответствует "золотое правило" Конфуция и нравственные императивы многих религий. Исследования показывают, что в эволюционном плане именно такая стратегия оказывается наиболее эффективной, постепенно обучая социум механизмам кооперации¹.

Отметим, что эволюционно эффективная стратегия не обязательно побеждает в каждом поединке с другими стратегиями. Более того, очевидно, что стратегия обмана, отказа от сотрудничества в каждой игре в принципе не может проиграть ни одного поединка. Но и очков эта стратегия приносит немного. Особенность турнира состоит в том, что лучше проиграть поединок со счетом 500:600, чем выиграть со счетом 200:100 очков. В этом случае понятно, что победить в турнире может стратегия, проигравшая абсолютно все личные поединки; это произойдет, если другие стратегии, встречаясь между собой, наберут относительно немного очков.

Анализ хода партий показал, что обычно стороны за первые несколько десятков ходов пытаются понять партнера, варьируя выбор альтернатив. Затем стороны выходят на стационарное состояние, т.е. выбирают один из вариантов (С;С либо D;D) и следуют ему до конца поединка. Ясно, что победителем турнира оказывается программа, быстрее других обучающая партнеров действовать кооперативно. Именно такой оказалась стратегия "Зуб за зуб", несмотря на то, что многие участники турнира специально готовились к борьбе с ней.

Аксельрод считает, что из результатов турнира следуют правила житейской мудрости:

• не будь завистлив;
• не обманывай первым;
• проявляй взаимность и в сотрудничестве и в обмане;,
• не будь слишком умным.

Отношение к социальному взаимодействию, как к игре с нулевой суммой (сколько один выиграл, столько другой проиграл) является

278

достаточно распространенным стереотипом. Однако в реальной жизни часто встречаются ситуации, в которых следование эгоистическим стратегиям неэффективно, что и доказывает исследование модели "Дилемма заключенного" для двух партнеров. Еще более интересные ситуации возникают при участии в играх п лиц.

В июне 1983г. Д. Хофстадтер озадачил читателей журнала "Scientific American", предложив им сыграть в игру с призовым фондом 1 млн (10⁶ ) долларов. Участники игры должны были прислать в редакцию журнала открытку с указанием какого-либо одного числа. Победителем будет тот, кто пришлет открытку с наибольшим числом. Игра "Наибольшее число" имеет очень любопытное правило награждения: победитель, назвавший наибольшее число N, получает выигрыш, равный, 10⁶/N. Остальные же участники не получают ничего. Если победителей будет двое, то выигрыш делится пополам. Таким образом, выигрыш вычисляется по следующей формуле: P/Nm, где Р- призовой фонд, N - наибольшее названное число, т - число участников, выбравших число N.

В игре приняло участие около 1000 читателей. Почти все прислали открытку с числом 1. Если бы так поступили все, то выигрыш каждого составил бы примерно 1000 долларов. Однако более предприимчивый читатель рассуждал иначе. Он считал, что большинство пришлют числа 1,2, может быть, 3 и поставил в открытке число 10, рассчитывая получить 100 000 долларов, оставив остальных с носом. Но таких предприимчивых оказалось довольно много. Более того, 33 человека прислали число 10⁶ , надеясь получить хотя бы 1 доллар. Однако несколько энтузиастов прислали числа порядка 10¹⁰⁰, сделав выигрыш исчезающе малым.

Моделям игр с участием п лиц посвящена обширная литература, в которой исследуются механизмы кооперирования, образования коалиций, процессы самоорганизации [1, 3, 6, 8]. В этих моделях исследуются условия возникновения социального порядка в условиях, когда участники не имеют полной информации о предпочтениях друг друга.

Задачи и упражнения

1. Постройте теоретико-игровые модели наиболее крупных конфликтов последних лет.
2. Постройте модель взаимодействия социальной системы и индивида.
3. Предположим, что на одном сегменте рынка действуют две конкурирующие фирмы. Каждая фирма может выбрать одну из двух альтернатив: С - разработать и внедрить инновацию; D - имитировать продукт, созданный другой фирмой (см. гл. 9). В данной модели предполагается, что имитация приносит больший доход, так как фирма не несет затрат, связанных с разработкой и внедрением инновации. Рассмотрим игру со следующей таблицей выигрышей [9]:

279

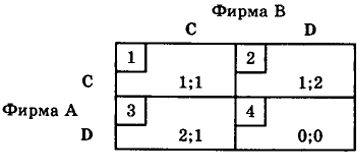
Какие стратегии в этой модели являются рациональными?

4. Сформулируйте определение эволюционно эффективной стратегии.
5. Авторы [7] присвоили имена некоторым стратегиям, разработанным для итеративной дилеммы заключенного: Сталина - стратегии постоянного отказа от сотрудничества, Ганди - стратегии постоянного сотрудничества, альтруизма, независимо от поведения партнера. Каким стратегиям можно присвоить имена Макиавелли, Чингисхана, Наполеона, современных политиков?
6. Проверьте сплоченность своей студенческой группы с помощью игры "Наибольшее число". Как поведут себя участники, если игру повторить несколько раз?

Литература

1. Воробьев Н.Н. Теория игр для экономистов и кибернетиков. М., 1985.
2. Миркин Б.Г. Проблема группового выбора. М.: Наука, 1974.
3. Мулея Э. Кооперативное принятие решений: Аксиомы и модели. М.:Мир, 1991.
4. Саати Т.Л. Математические модели конфликтных ситуаций. М., 1977.
5. Axelrod R. The Evolution of Cooperation, N.Y.: Basic Books, 1984.
6. Handbook of Game Theory with Economic Application. L., 1992.
7. Krains D., Krains V. Pavlov and Prisoner's Dilemma // Theory and decision. 1989. Vol. 26. № 1. P. 47-79.
8. Rapoport A. Decision Theory and Decision Behaviour. Normative and Descriptive Approach. Dordrecht: Kluer Acad. Publ. 1989.
9. Rasmusen E. Games and Information. Cambridge: Blackwell, 1994.

280