Центральной проблемой когнитологии - выбором индивидом наиболее эффективных, оптимальных альтернатив занимается теория принятия решений, которая первоначально считалась ветвью исследования операций, а сейчас рассматривается как область системного анализа. Наиболее продвинутой частью теории являются задачи с единственным критерием эффективности. Значительно сложнее обстоит дело, если в задаче имеется несколько критериев эффективности. Но наиболее сложные проблемы возникают в том случае, если в принятии решений участвуют несколько сторон, каждая из которых имеет собственные критерии выбора предпочтительных решений, причем эти критерии могут полностью или частично противоречить друг другу. Именно такие модели конфликта критериев рассматривает теория игр.
По числу приложений в социальных науках явно лидирует модель, называемая по традиции "Дилемма заключенного". Рассматривается проблемная ситуация, в которую вовлечены только два участника - А и В (два индивида, индивид и система или две социальные системы). Игра состоит в том, что каждый участник выбирает одну из двух альтернатив:
- С - сотрудничество, кооперация, солидарность, учет общих интересов, разрешение конфликта, альтруистическое поведение;
- D - отказ от сотрудничества, усиление конфронтации, обман, нарушение принятых норм, правил, обязательств, эгоистическое поведение.
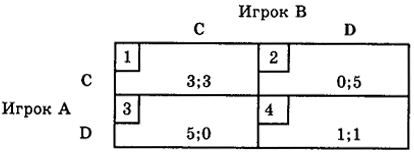
Результаты игры определяются с помощью следующей таблицы выигрышей (платежной матрицы).
В данном примере, если оба игрока выберут стратегию кооперации С, то получаемый каждым выигрыш задается в клетке 1. В клетках содержатся по два числа. Первое число - это выигрыш первого игрока (А), второе число - выигрыш второго игрока (В). Проигрыш игрока задается отрицательным числом.
273
В зависимости от соотношения чисел в таблице выигрышей каждый игрок пытается определить наиболее рациональную линию поведения. В рассматриваемом примере оба игрока знают, что выбор стратегии кооперации С дает любому из них три единицы выигрыша, допустим 3 руб. Если оба откажутся от кооперации С, обманут (альтернатива D), то получат только по 1 руб. В клетке 2 содержится исход игры в случае, когда игрок А выбирает сотрудничество, а игрок В - обман. Тогда игрок А не получает ничего, а игрок В выигрывает 5 руб. В клетке 3 описан противоположный исход. Если игрок А решается на обман, а игрок В выбирает сотрудничество, то выигрыш первого составляет 5 руб., а второй не получает ничего.
В теории игр для данных исходов приняты стандартные обозначения R, Т, S, Р, где R - награда за взаимное сотрудничество, Т - цена "предательства", S - плата неудачнику, а. Р - наказание за обоюдный обман. В нашем примере R = 3, Т = 5, 8 = 0, Р=1.
С точки зрения коллективных интересов лучшим является вариант взаимного сотрудничества (С,С), который приносит в сумме 6 руб., что значительно лучше, чем вариант взаимного обмана (D,D), позволяющий получить в сумме только 2 руб. Однако попытка взглянуть на ситуацию с точки зрения индивидуальной рациональности приводит к другому результату. Игрок А, просчитывая ситуацию в уме, видит, что выбор альтернативы С в худшем случае дает только ноль, если В обманет его ожидания и выберет альтернативу D. Предполагая, что игрок В выбирает альтернативы с равной вероятностью 0,5, игрок А может получить в среднем 1,5 руб. Продолжая рассуждение, игрок А оценивает последствия выбора им альтернативы D. С одной стороны, имеется соблазн поживиться за счет партнера и получить максимальный выигрыш - 5 руб. С другой стороны, в худшем случае игрок А получает 1 руб., в среднем же 3 руб., т.е. по обоим показателям альтернатива D выглядит предпочтительнее, чем С. Со своей стороны, игрок В рассуждает аналогичным образом, что в результате приводит к выбору неэффективного с коллективной точки зрения решения (D, D).
Таким образом, в голове индивида А формируются как бы две когнитивные модели ситуации - одна модель отражает его собственные интересы, другая - коллективные, т.е. интересы системы в целом1. Конфликт между моделями создает когнитивный диссонанс [8], разрешение которого в данном случае зависит
274
только от соотношения параметров R, Т, Р, S. Стратегическая структура игры "Дилемма заключенного" сохраняется при условии, что Т > R > Р > S.
Среди приложений теории игр важное место занимает модель "Петухи" (Chicken game). Ее стратегическая структура определяется соотношением Т > R > S > Р. Своим названием игра обязана забавам лихачей-водителей. Два водителя мчатся навстречу друг другу. Проигравшим считается тот, кто первым струсит и свернет в сторону.
С помощью этой модели политологи исследуют развитие Карибского кризиса 1962 г., вызванного размещением советских ракет на Кубе. Предположим, что каждая из сторон (СССР и США) имеет только две альтернативы действий, а таблица выигрышей выглядит следующим образом:
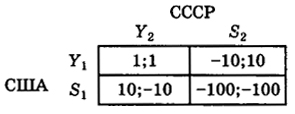
После размещения на Кубе советских ракет и введения США морской блокады у сторон есть две основные альтернативы - переговоры и поиск взаимоприемлемых компромиссов (вариант Y1 ) либо твердое отстаивание своих позиций с неизбежной эскалацией конфликта (вариант Sj). Если США выберут альтернативу S1 (в данном случае планировалась бомбардировка ракетных площадок на Кубе), то в случае ухода СССР побеждает США - вариант (S1; Y2). Если же СССР продолжает следовать твердой линии, то неизбежен вариант (S1;S2), т.е. в данном случае - ядерная война, в которой обе стороны теряют не только лицо, но и все остальное. При принятия США мягкой, компромиссной стратегии YJ и твердого отстаивания СССР своей позиции имеет место вариант (Y1; S2) - побеждает СССР.
Попробуйте самостоятельно проанализировать наиболее разумные стратегии поведения сторон в этой ситуации. Следует заметить, что в таких играх нередко побеждают игроки, имеющие репутацию не рациональных, а бесшабашных, готовых на любой риск головорезов.
Важные черты переговорного процесса моделирует игра "Семейный спор" [4]. Предположим, что муж с женой выбирают, как провести воскресный вечер - пойти на футбол или в театр. Муж предпочитает футбол, а жена театр, но проведение вечера врозь
275
не нравится обоим. Таблица выигрышей в таком случае может выглядеть следующим образом:

Из таблицы видно, что варианты раздельного отдыха следует отбросить. Но совместные походы на футбол или в театр приносят одинаковую коллективную полезность. Какой же вариант следует предпочесть? Лучше всего пойти куда-нибудь вместе, чтобы был доволен один, а в следующий раз удовлетворить желание другого члена семьи.
Таким образом, выход из этой конфликтной ситуации легко найти, если перейти от статического рассмотрения проблемы к динамике. Попробуем применить этот прием к анализу "Дилеммы заключенного".
276
1
Для принятия решений индивид также строит различные модели поведения партнера.
