Любопытную историю развития нового направления моделирования начали математики, с удовольствием изучавшие необычную абстрактную конструкцию - клеточный автомат. В 70-е годы началось повальное увлечение играми (типа игры "Жизнь"). Но постепенно стали появляться более интересные области приложения, в основном в естественно-научной сфере. Американский математик Дж. фон Нейман полагал, что такие сложные процессы, как самовоспроизведение, морфогенез, турбулентность, целесообразно моделировать с помощью клеточных автоматов. Появляется все больше примеров успешного использования нового языка для моделирования социальных процессов. А в последние годы речь идет уже
260
о появлении новых универсальных моделей реальности [1], созданы даже машины клеточных автоматов - приставки к ЭВМ, существенно ускоряющие процесс моделирования [5].
В данной главе читатель познакомится с тем, как строить реалистические модели социальных процессов и, главное, как их можно без особых усилий реализовать с помощью обычных электронных таблиц (в данном случае Excel). После этого процесс исследования модели сводится к изучению последовательности картинок, получаемых нажатием одной кнопки.
Клеточными автоматами принято называть сети из элементов, меняющих свое состояние в дискретные моменты времени [3]. Чаще всего рассматриваются двумерные клеточные автоматы, элементом которых является один квадрат (например, на листе бумаги в клетку). Каждый автомат или клетка может находиться в конечном числе состояний, в простейшем случае в двух - черное или белое, жизнь или смерть, 1 или 0. Время в модели задается дискретным множеством тактов (t = 1, 2, 3, ...). Система клеточных автоматов, как правило, функционирует в некотором замкнутом пространстве (например, в квадратной решетке 10×10 или 100×100), Состояние автомата в момент t + 1 определяется его состоянием и состоянием его ближайших соседей в предыдущий момент t.
В моделях клеточных автоматов среда обычно предполагается однородной, т.е. правило изменения состояний для всех клеток одинаковы. Если это правило не зависит от случайных факторов, то автомат называется детерминированным, если зависит - то стохастическим.
Рассматриваются также клеточные автоматы с памятью. В этом случае состояние элемента в момент t + 1 зависит от состояния системы в моменты t и t - 1 (таким образом учитывается эффект запаздывания).
Одним из наиболее важных понятий теории клеточных автоматов является понятие окрестности, т.е. множества клеток, которые считаются "соседними" с данной клеткой. На рис. 14.1 приведены
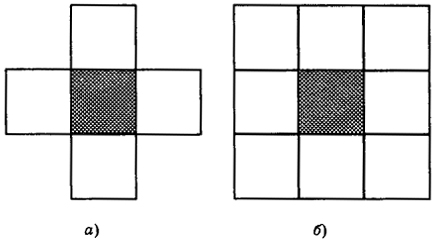
Рис.14.1. Окрестности фон Неймана (а) и Мура
(б)
261
два наиболее распространенных типа окрестности автомата, расположенного в заштрихованной клетке.
Для того чтобы дальнейшее изложение не показалось читателю чересчур абстрактным, приведем пример моделирования процесса расовой сегрегации [9].
Предположим, что исследуемый регион может быть представлен решеткой 16x13, где каждая клетка соответствует одному дому. Предположим также, что каждый дом может быть занят белой (о) или черной (х) семьей, либо остаться пустым. В данной модели у каждого клеточного автомата есть три возможных состояния, а общее число состояний модели составит примерно 1099.
В рассматриваемом примере предполагается, что каждая расовая группа предпочитает иметь определенный процент соседей с тем же цветом кожи. Если это условие не выполняется, то семья перебирается в ближайший дом, где процентный состав соседей яввляется приемлемым. Считается, что разумный выбор можно сделать, если в данном поселении 25-30% домов не заселены. Начальная структура расселения приведена на рис. 14.2.

Рис. 14.2. Начальная структура расселения
В [9] рассматривались два правила поведения жителей, оценивающих процент приемлемых соседей (использовалась окрестность Мура):
- 1) не менее половины соседних домов должны быть заселены представителями той же расы;
- 2) не менее трети соседей принадлежат той же расе.
На рис. 14.3,а приведен результат моделирования при использовании первого правила. Как видно из рисунка, в модели постепенно происходит процесс разделения региона на несколько расово-однородных областей.
Результат моделирования с менее жестким вторым правилом демонстрирует неструктурированный вариант расселения, близкий к начальному состоянию (рис. 14.3,b).
Так что же произошло с исследуемой системой? Руководствуясь только локальными правилами поведения (1), задаваемыми на микроуровне каждой семьи без какого-либо централизованного руководства и сговора, процесс переселения стихийно самоорганизовался,
262

Рис. 14.3. Эволюция системы расселения
и в результате спонтанно родилась достаточно четкая структура расселения (см. рис. 14.3, а).
Приведенный чрезвычайно упрощенный пример показывает, что клеточное моделирование дает в руки исследователя мощный инструмент для изучения процессов социальной самоорганизации. Анализ поведения клеточных автоматов показал, что их эволюция во многом аналогична динамике сложных нелинейных систем, рассмотренных в гл. 12 и 13. Выделяют четыре основных класса автоматов [3]:
- Независимо от начального состояния за конечное число шагов происходит переход к однородному состоянию - все автоматы оказываются в состоянии покоя.
- В процессе эволюции автомат приходит к локализованным стационарным или периодическим решениям.
- Картины активности системы автоматов являются апериодическими - никогда не повторяются. Можно сказать, что автоматы демонстрируют хаотическое поведение.
- Динамика автоматов существенно зависит от начального состояния. Подбирая различные начальные состояния, можно получать самые разнообразные конфигурации и типы поведения.
Примером автомата четвертого типа является игра "Жизнь", изобретенная математиком из Кембриджского университета Дж. Конвеем. Название связано с тем, что возникающие в процессе игры ситуации аналогичны реальным процессам зарождения, развития и гибели колоний живых организмов. Основная идея игры заключается в том, чтобы, начав с произвольно заданного исходного положения, проследить за эволюцией исходной позиции под действием "генетических законов" Конвея, которые управляют рождением, гибелью и выживанием "организмов".
263
Игра проводится на бесконечной плоской решетке квадратных клеток и состоит из шагов, соответствующих дискретному времени (t = 1, 2, ... ). Один ход в игре - это переход из состояния t в состояние t +1. Каждая клетка может быть "живой" или "мертвой". Изменение состояния клетки в момент t+1 однозначно определяется состоянием ее соседей в предыдущий момент t. У каждой клетки восемь соседей, из которых четыре имеют с ней общие ребра, а четыре общие вершины.
Назовем "потенциалом" клетки - число живых соседей, используя определение окрестности по Муру. Тогда генетические законы Конвея, определяющие поведение каждой клетки, сводятся к следующим правилам:
- если потенциал равен 2, то состояние клетки не меняется;
- если потенциал равен 3, то клетка в следующий период будет живой независимо от текущего состояния;
- при остальных значениях потенциала (0, 1, 4, 5, 6, 7) клетка в следующий период будет мертва.
Таким образом, если у клетки более трех живых соседей, то она погибает от перенаселенности. Клетка погибает от одиночества, если жива только одна соседняя клетка или все соседние клетки мертвы. Выживает и переходит в следующее поколение клетка, имеющая двух или трех живых соседей.
Имея под рукой лист бумаги в клетку, читатель может убедиться, что любая начальная популяция претерпевает необычные и неожиданные изменения. Некоторые первоначальные колонии организмов постепенно вымирают, однако большинство исходных конфигураций либо переходит в стационарные структуры, не зависящие от времени, либо наступает колебательный режим.
Читатель может также легко убедиться, что конфигурации, изображенные на рис. 14.4, а, погибают на втором ходу, тогда как три конфигурации на рис. 14.4, б являются стационарными (эти конфигурации имеют названия: левая - "блок", центральная - "бадья", правая - "змея").
На рис. 14.4, в изображена эволюция конфигурации, называемой "мигалкой" или "семафором"; ее цикл равен 2. Еще два примера циклических конфигураций с периодом 2 приведены на рис. 14.4, г. Больший период (соответственно 4 и 5) имеют конфигурации, изображенные на рис. 14.4, д и е. Построены конфигурации, имеющие значительно больший период колебаний.
После первых публикаций в популярных изданиях М. Гарднера, посвященных игре "Жизнь", произошел взрыв энтузиазма среди пользователей ЭВМ. Затраты машинного времени на исследование
264

Рис. 14.4. Конфигурация: игры "Жизнь."
различных вариантов игры составили миллионы долларов. Были выявлены многочисленные замечательные конфигурации, одна из которых, называемая "планер" (глайдер), приведена на рис. 14.4, ж. Через каждые четыре шага планер повторяет себя, смещаясь на одну клетку вниз и вправо, т.е. движется по диагонали. Найдены конфигурации, которые могут двигаться по прямой. В 1970 г. обнаружена конфигурация "катапульта", которая через каждые 30 шагов повторяет себя и "выстреливает" планер.
В процессе исследований выяснилось, что с помощью игры "Жизнь" можно не только изучать процессы эволюции, но и моделировать основные компоненты современных ЭВМ, исследовать прообразы параллельно'работающих ЭВМ, решать задачи распознавания образов.
Данная ветвь синергетики относится к теории коллективного поведения автоматов [3], но все-таки наибольший интерес исследователей привлекают проблемы самоорганизации в биологических системах, формализованных на языке динамических систем.
Игра "Жизнь" была популярна в 70-80-е годы, а в 90-е годы появилось новое популярное развлечение - игра "Ант" (термит), изобретенная американским математиком К. Лангтоном [6]. Клеточный автомат в этой игре может иметь два состояния - черное
265
и белое. Игра происходит на поле из квадратных клеток, которые в начальном состоянии все имеют белый цвет.
Ант стартует с центральной клетки в некотором выбранном направлении, например на Восток, переходит на соседний квадрат и смотрит: если этот квадрат черный, то Ант красит его в белый цвет, а сам поворачивает налево на 90´. Если квадрат окажется белым, то Ант делает его черным и поворачивает направо на 90´ и т.д.
Оказывается этот примитивный автомат демонстрирует очень сложное поведение. Пройдя приблизительно 500 шагов, он возвращается в центральную клетку, оставляя после себя ряд симметричных орнаментов. Но после примерно 10 000 шагов картина становится весьма хаотичной. Ант неожиданно начинает строить магистраль - повторяя цикл из 104 шагов, он формирует диагональ, идущую на юго-запад. Интересно, что поведение автомата остается таким же, если в начальном положении имеется много черных квадратов.
266
