13.2. Портреты хаоса

Для того чтобы интуитивно понять основные концепции теории хаоса, не обязательно штудировать тома математической литературы. Достаточно провести несколько экспериментов, доступных любому студенту, знакомому с основными возможностями электронных таблиц (см. § 12.1).

Исследуем поведение решений следующего логистического разностного уравнения:

Здесь предполагается, что емкость рынка равна 1, поэтому 0 ≤ х_t ≤ 1, т.е. x_t - это доля рынка, завоеванная новинкой к моменту t; λ, - параметр управления [7].

Исследуем поведение системы (13.6) с помощью Excel, но несколько модифицируем схему вычислений. Столбец А сформируем так же, как и в § 12.1, параметр А, запишем в ячейку С1. Сформируем вспомогательный столбец В, равный столбцу А, но со сдвигом на одну ячейку вниз (табл. 13.1).

Таблица 13.1. Фрагмент окна Excel

В данной таблице в ячейку А1 введено начальное значение х₁ = = 0,85, в ячейку В1 записан 0, а в ячейке С1 будет храниться значение параметра X. В ячейке А2 записана рекуррентная формула логистического уравнения, а в ячейке В2 указывается, что значение числа следует взять из предыдущей строки столбца А. Выделим ячейки А2 и В2. Затем размножим формулы в этих ячейках вниз до строки 60.

Построим график поведения решения уравнения (13.6) так же, как это делалось в § 12.1. Построим еще один график, отражающий

255

поведение системы в фазовой плоскости (у,х) - в данном случае (x_t+1, x_t). Для этого выделим 60 строк в столбцах А и В. Вызовем меню "мастер диаграмм". Выберем тип диаграммы (Точечная), и в раскрывшейся галерее выберем вариант диаграммы со значениями, соединенными сглаживающими линиями. Полученный график поместим под ранее построенной диаграммой. Теперь изменения в поведении системы будут видны одновременно в двух вариантах графиков.

Изменим поведение системы (13.6), варьируя значения управляющего параметра в интервале от 0 до 4. При этом система демонстрирует три различных типа поведения: 1) стремление к состоянию равновесия; 2) периодические колебания; 3) хаос.

При значении λ, от 0 до 3 система стремится к равновесному стабильному положению (пример на рис. 13.5). Посмотрите, как ведут себя графики при λ, = 0,5; 1,8; 2,2; 2,6. При λ, < 1 наступает положение равновесия: х*= 0. При 1< λ,< 3 система стремится к стационарному состоянию: x*=l - (1/λ,). Полезно при фиксированном А. поэкспериментировать с разными начальными состояниями (Xj).

Рис. 13.5. Стремление к состоянию равновесия (λ = 2,2)

Периодические колебания охватывают систему при λ > 3. Качественное изменение поведения системы говорит о том, что λ = 3 является точкой бифуркации - положение равновесия сменяется предельным циклом. Зададим λ = 3,2 и увидим, что довольно быстро система переходит к колебаниям с периодом 2 (в столбце А остаются только два чередующихся значения) (пример на рис. 13.6). Постепенно увеличим значение λ = 3,3; 3,4; 3,5. При λ = 3,5 период колебаний равен 4 - произошло удвоение периода. При λ = 3,567 появляется цикл с периодом 8. При

256

дальнейшем росте λ появляются циклы с периодом 32, 64, 128, 256 и т.д. [7].

В хаотический режим система попадает при λ ∈ (3,8;...4) (рис. 13.7). Поведение системы становится апериодическим, не видно какой-либо закономерности. Поведение кажется случайным, подверженным непредсказуемым внешним воздействиям. На самом деле это загадочное поведение полностью определено детерминированным законом функционирования системы (13.6). Но прогнозировать поведение системы в состоянии хаоса на длительный период времени невозможно. Хаотическое поведение слишком чувствительно к изменению исходных данных. Изменение х₁ на одну миллионную может существенно изменить ход решения.

Качественное изменение режимов функционирования системы удобно наблюдать в фазовой плоскости. В варианте сходимости к

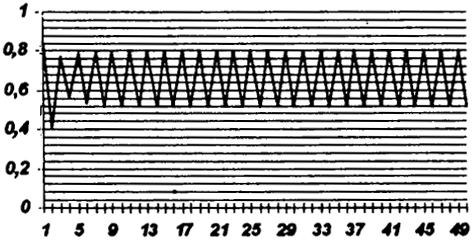
Рис. 13.6. Колебания с периодом 2 (λ = 3,2)

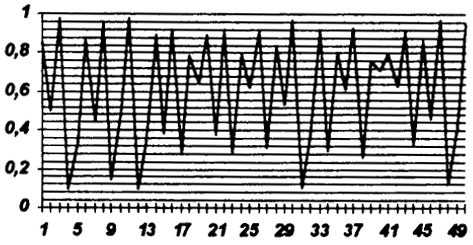
Рис. 13.7. Хаотический режим (λ = 3,9)

257

положению равновесия решения стремятся к одной точке. Для колебаний с периодом 2 аттрактором является цикл, состоящий из двух точек. Значительно более запутанная картина возникает в случае хаотического режима. Рассмотрим несколько вариантов графика. Для этого следует отредактировать диаграмму, щелкнув по ней правой кнопкой мыши. Появится контекстное меню, в котором следует выбрать опцию "Тип диаграммы". Появится галерея вариантов графика. Выберем вариант даграммы без маркеров и увидим типичную картинку странного аттрактора (рис. 13.8).

Рис. 13.8. Хаотический режим в фазовой плоскости (λ = 3,9)

Теперь уберем лишние линии, выбрав первый вариант графика, и перед нами окажется портрет таинственного странного аттрактора (рис. 13.9). Именно по этому множеству точек хаотично "скачет" исследуемая система. И ее можно понять - в данном случае странный аттрактор имеет вполне притягательную параболическую форму.

Поэкспериментируйте с различными исходными данными и понаблюдайте за эволюцией странного аттрактора. Убедитесь, что в хаосе тоже существует своего рода порядок.

Еще менее устойчивым становится поведение систем при учете эффекта запаздывания. Рассмотрим следующий вариант логистического уравнения:

В этом случае состояние системы в момент t + 1 зависит не только от x_t, но и от x_{t - 1}. Вспоминая, как исследуются такие модели (см. задачу Фибоначчи в § 12.1), составим вычислительную

258

Рис 13.9. Портрет странного аттрактора (λ = 3,9)

модель (аналогично предыдущему случаю). Оказывается, система (13.7) имеет положение равновесия только при 0 < λ < 2. При λ = 2 происходит бифуркация и появляется предельный цикл. При λ > 2,27 поведение системы перестает быть стабильным [5,6].

♦♦♦

Что же дает социологу исследование нелинейных моделей социальных систем? Проведение вычислительных экспериментов позволяет определить границы параметров, при которых система устойчиво демонстрирует стабильное поведение. Даже если система оказалась в состоянии хаоса, исследование формы странного аттрактора может дать полезную информацию.

Результаты последних лет позволяют надеяться, что и хаотическими ситуациями можно научиться управлять. Используя чувствительность хаотических режимов, в некоторых случаях удается легко перейти на стабильные траектории развития [7].

Задачи и упражнения

1. Исследуйте поведение системы, описываемой следующим нелинейным разностным уравнением:

259

2. Попробуйте варьировать значения параметров модели из задачи 1.
3. Проведите вычислительные эксперименты с разностными аналогами системы Лотки-Вольтерра, варьируя типы взаимодействий.
4. Исследуйте разностное уравнение x_t+1 = 3,6 x_t - x_t²при 0 < x₁ < 3,6. Имеет ли система хаотический режим?
5. Исследуйте разностное уравнение с запаздыванием:

xt+1 = λx_{t - 1} (1 - x_t).

Литература

1. Арнольд В.И. Теория катастроф. М., 1990.
2. Гласе Л., Мэки М. От часов к хаосу. Ритмы жизни. М.: Мир, 1991.
3. Новое в синергетике, Загадки мира неравновесных структур. М.: Наука, 1996.
4. Самарский А.А., Михайлов А.П. Курс математического моделирования. М.: Наука, 1997.
5. Bhargava S. et al. Some Comments on Chaos and Fractals // Technological Forecasting and Social Change. 1990. Vol. 38, № 2. P. 323-331.
6. Gordon Т., Greenspan O. The management of Chaotic Systems // Technological Forecasting and Social Change. 1994. Vol. 47. № 1. P. 49-62.
7. Kiel L.P., Elliott E. Exploring Nonlinear Dynamics with Spreadsheet: A Graphical View of Chaos for Beginners // Chaos Theory in the Social Sciences / Ed.by L.D.Kiel and E.Elliot. Ann Arbor: The Univ. of Michigan Press. 1996. P. 19-29.

260