Рассмотрим следующую ситуацию, в которой могут оказаться две враждующие страны. Первая страна ("желтые") вооружается, опасаясь потенциальной угрозы войны с соседней враждебной страной ("зеленые"). В свою очередь "зеленые", зная о росте затрат на вооружение у "желтых", также увеличивают расходы на вооружение. Предположим, что каждая страна изменяет скорость роста (сокращения) вооружений пропорционально уровню затрат другой. Математически эта ситуация может быть смоделирована
238
следующим образом. Пусть x(t) - расходы на вооружение "желтых" к моменту t ≥ 0, y(t) - то же, но "зеленых". Тогда простейшая модель гонки вооружений может быть сформулирована в виде системы двух линейных дифференциальных уравнений с постоянными коэффициентами:
| { |
dx / dt = ay, |
| dy / dt = bx, |
(12.16)
где а и b - положительные константы. Эти уравнения описывают положительную обратную связь.
Модель (12.16) имеет очевидный недостаток: рост затрат на вооружение ничем не лимитируется. Естественно предположить, что чем больше текущий уровень затрат на оборону, тем меньше скорость его роста (отрицательная обратная связь). Получаем следующую систему уравнений:
| { |
dx / dt = ay-mx, |
| dy / dt = bx - пу, |
(12.17)
где а, b, т, п - положительные константы.
Рассмотрим третий постулат, включенный Л. Ричардсоном в модель: государство наращивает вооружение, руководствуясь своими державными притязаниями и враждебностью к другим государствам, даже если другие страны не угрожают существованию данного государства. Обозначим соответствующие коэффициенты претензии через r и s (r > 0 и s > 0). Если г<0 и s < 0, то их можно назвать коэффициентами доброй роли. Получаем следующую систему уравнений:
| { |
dx / dt = ay - тх + r, |
| dy / dt = bx - ny + s, |
(12.18)
Решением системы (12.18) являются функции x(t) и y(t), определяемые для данных начальных условий х0, у0 (начальное состояние гонки вооружений) [13, 24-26].
Элементарный анализ модели. Одним из важнейших свойств, которые "разумно" потребовать от гонки вооружений, является стабильность. Формализуем это требование следующим образом.
239
Уровень затрат на вооружение должен быть постоянным и не зависеть от времени:
dx/dt = dy/dt = 0,
(12.19)
т.е. желательно, чтобы система находилась в состоянии равновесия.
Условия равновесия для системы (12.18) записываются в следующем виде:
ау - тх + r = 0,
(12.20)
bx - ny + s - 0.
(12.21)
Из (12.20) определим
у = (т/а)х - r/а
(12.22)
и рассмотрим геометрическую интерпретацию линейного уравнения (12.22) на фазовой плоскости (х, у) (рис. 12.7).
Для всех точек прямой G имеем dx/dt = 0. Можно сказать, что первое уравнение системы (12.18) задает горизонтальную компоненту скорости движения точки в фазовой плоскости, а второе уравнение - вертикальную. Ясно, что если в некоторой точке фазовой плоскости dx/dt > 0, то x(t) возрастает и решение системы движется от этой точки вправо, а если dx/dt < 0, то влево. Аналогично, если dy/dt > 0 (< 0), то точка движется вверх (вниз).
Из школьного курса алгебры известно, что прямая G делит плоскость (х, у) на две полуплоскости. Для всех точек одной
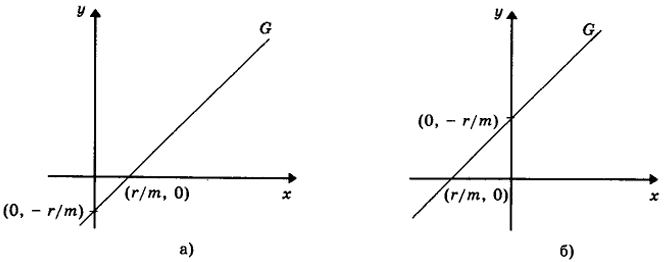
Рис. 12.7. Геометрическая интерпретация уравнения (12.22):
а - при
r > 0;
б - при
r < 0
240
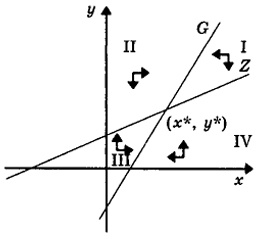
Рис. 12.8. Точка равновесия в первом квадранте
полуплоскости dx/dt > 0, а другой полуплоскости dx/dt < 0. То есть первое уравнение системы (12.18) как бы заставляет точки притягиваться по горизонтали к прямой G. Аналогичное утверждение верно для второго уравнения этой системы и прямой Z (вертикальное притяжение) (рис. 12.8). Прямые G и Z делят первый квадрант на четыре области, обозначенные римскими цифрами I, II, III, IV.
Рассмотрим поведение модели Ричардсона при t →∞. Возможны три случая:
1. Бесконечная гонка вооружений: х →∞ и у →∞.
2. Взаимное разоружение: х → 0, у → 0.
3. Равновесие вооружений: х → х*, у→ у*, где у*, х* > 0. Точка равновесия (х*, у*) находится на пересечении прямых G [уравнение (12.20)] и Z [уравнение (12.21)] (см. рис. 12.8).
Легко показать, что если r > 0 и s > 0,то точка пересечения G и Z лежит в первом (см. рис. 12.8) или третьем (рис. 12.9) квадранте.
Стрелки на рис. 12.8-12.10 показывают горизонтальную и вертикальную составляющие движения точки, находящейся в той или иной области фазовой плоскости. В варианте, показаном на рис. 12.8, из любой начальной точки решение со временем приходит в точку равновесия, достигается "баланс сил", причем независимо от начального уровня вооружений. Из рис. 12.9 видно, что если начальная точка попала в область II, то х →∞ и у →∞.
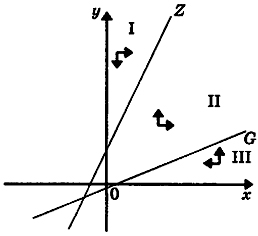
Рис. 12.9. Точка равновесия в третьем квадранте
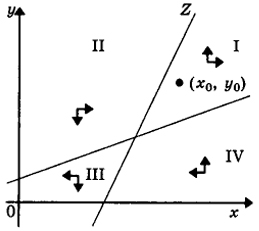
Рис. 12.10. Поведение системы при
r < 0 или (и)
s < 0
241
Рассмотрим ситуацию, когда по меньшей мере один из коэффициентов r, s < 0 (рис. 12.10).
Если начальный уровень затрат, т.е. точка (х0, у0), находится в области I, то гонка вооружений будет бесконечной (х -"´´, у -> ´´). Если начальная точка находится в области III, то решение системы (12.18) также "уходит" от равновесия (х*, у*), но зато стремится к точке (0, 0) (взаимное разоружение).
Таким образом, наличие у одного или обоих государств "доброй воли" (r, s < 0) не гарантирует удовлетворительного исхода гонки вооружений. Все зависит от начального состояния системы.
Очевидно, что поведение модели Ричардсона зависит от соотношения коэффициентов а, b, т, п и знаков r, s. Читателю предлагается самостоятельно убедиться, что имеют место четыре возможных случая:
- Если тп - ab > 0, r > 0, s > 0, то существует точка равновесия.
- Если тп - ab < 0, r > 0, s > 0, то логика модели ведет к неограниченной эскалации гонки вооружений.
- Если тп - ab > 0, r < 0, s < 0, то гарантируется полное взаимное разоружение.
- Если тп - ab < 0, r < 0, s < 0, то пессимистичность или оптимистичность прогноза существенно зависит от начального состояния.
Для проверки своей достаточно упрощенной модели Ричардсон собрал данные о гонке вооружений перед первой мировой войной (1909-1913 гг.). Изучая противоборство двух блоков (х - Франция и Россия, у - Германия и Австро-Венгрия, расходы Англии, Италии и Турции не учитывались), Ричардсон составил таблицу военных бюджетов для четырех стран (все затраты даны в миллионах фунтов стерлингов) (табл. 12.3).
Таблица 12.3. Расходы на вооружение
| Страна |
1909 |
1910 |
1911 |
1912 |
1913 |
| Франция |
48,6 |
50,9 |
57,1 |
63,2 |
74,7 |
| Россия |
66,7 |
68,5 |
70,7 |
81,8 |
92,7 |
| Германия |
63,1 |
62,0 |
62,0 |
68,2 |
95,4 |
| Австро-Венгрия |
20,8 |
204,8 |
214,9 |
238,7 |
289,0 |
| Сумма |
199,2 |
204,8 |
214,9 |
238,7 |
289,0 |
| Рост |
5,6 |
10,1 |
23,8 |
50,3 |
| Среднее за 2 года |
202,0 |
209,8 |
226,8 |
263,8 |
242
Чтобы сравнить модель с реальными данными, Ричардсон предположил, что а = b и т = п. Тогда уравнения (12.18) можно записать следующим образом:
dx/dt = ау -тх+г,
dy/dt = ax-my+s.
Сложив эти два уравнения, получаем
d(x+y)/dt = (а- т)(х+у) + (r+s).
Положим х+у = r, а-т = k, r+s = f, тогда
dz/dt = kz+f.
(12.23)
Общее решение этого уравнения записывается следующим образом:
z(t) = (z0+f/k)ekt - Hk,
(12.24)
где z - суммарные затраты на вооружение двух блоков; z0 - начальное состояние.
Рассмотрим поведение решения (12.24) в зависимости от соотношения коэффициентов. Если а < m, то k < 0, следовательно, первый член правой части соотношения (12.24) стремится к нулю при t →∞ и решение асимптотически стремится к значению (-f/k).
Если а > т, то k > 0 и z(t) экспоненциально растет. На рис. 12.11 ось абсцисс соответствует суммарному военному бюджету Франции, России, Германии и Австро-Венгрии в годы, предшествующие первой мировой войне (z). Ось ординат соответствует темпам роста расходов на вооружение (Δz/Δt).
Отмеченные на рис. 12.11 четыре точки соответствуют данным из табл. 12.3. Легко видеть, что все они лежат на одной прямой, что вполне соответствует соотношению (12.23), и, следовательно, модель Ричардсона достаточно достоверно описывает рассматриваемую ситуацию.
Известный американский математик Т. Саати считает, что "приведенная выше модель представляется
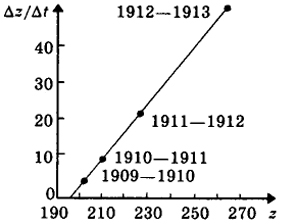
Рис. 12.11. Скорость роста затрат на вооружение
243
гораздо более убедительной, если вместо вооружений провести на ней изучение проблем угрозы, поскольку люди реагируют на абсолютный уровень враждебности, проявляемый по отношению к ним другими, и испытывают чувство тревоги в степени, пропорциональной уровню враждебности, которую они сами испытывают. Примечательной чертой такой модели является точно выраженная зависимость уровня вооружений одной стороны от уровня вооружений другой. Это позволяет каждой стороне корректировать уровень собственных вооружений по реакции ее потенциальных противников на уровень ее вооружений в прошлом" [13, с. 92].
Политологи установили, что для анализа большинства серьезных международных конфликтов за последние 200 лет можно использовать модель Ричардсона. Оказалось, что из 30 конфликтов, сопровождавшихся гонкой вооружений, 25 закончились войной. При отсутствии гонки вооружений только три из 70 конфликтов привели к войне.
Отметим, что гонка вооружений может закончится вполне мирно в случае экономического краха одной из враждующих сторон. Аналогичные модели применялись для анализа динамики предвыборных расходов и прогнозирования поведения участников аукционов.
244
