12.3. Основные понятия теории дифференциальных уравнений

Дифференциальные уравнения содержат не только функции, но и их производные. Запишем разностные уравнения, рассмотренные в предыдущем параграфе, в следующем виде:

Здесь Δt = 1. Уравнение (12.11) связывает состояние динамической системы в двух точках: t и (t + Δt). Перейдя в левой части этого уравнения к пределу при Δt - → 0, получим

Уравнение (12.12) является дифференциальным, разрешенным относительно производной.

Будем рассматривать только функции времени M(t), хотя в общем случае это не обязательно. Отметим, что дифференциальное уравнение в отличие от разностного описывает динамику поведения системы в каждой точке t. Уравнение (12.12) функционально связывает скорости изменения (производные по t) величин, характеризующих поведение системы, с самими величинами M(t).

Не отыскивая решения аналитически, в виде формулы, можно составить представление об общей картине этих решений на основе геометрического смысла уравнения (12.12). Напомним геометрический смысл производной dM/dt. В плоскости (M,t) для кривой M(t) величина dM/dt равна тангенсу угла наклона касательной к кривой. Следовательно, зная зависимость dM/dt от переменных M, t, выраженную уравнением (12.12), можно найти направление касательной к кривой, являющейся графиком решения данного уравнения.

Направление касательной можно показать на рисунке, проведя через любую точку (M,t) маленький отрезок прямой под углом φ так, что tgφ = f(M, t) (рис.12.3).

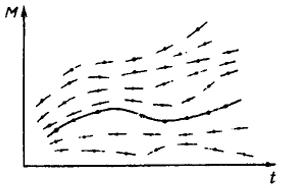
Рис. 12.3. Геометрическая интерпретация решений дифференциального уравнения

233

Если увеличить число точек, в которых проведено направление касательной, то, как видно из рисунка, образуется множество кривых, являющихся решением дифференциального уравнения (12.12). Это уравнение имеет бесконечное множество решений, а через каждую точку (М₀, t₀) плоскости проходит одно решение. Таким образом, для того чтобы получить конкретное решение уравнения, надо задать начальное условие (М₀, t₀).

Решением дифференциального уравнения называется функция, которая, будучи подставлена в это уравнение, обращает его в тождество. Графики решения дифференциального уравнения называются интегральными линиями этого уравнения. Рассмотрим несколько примеров.

Занимаясь вопросами наукометрии, В.В. Налимов сформулировал две модели развития науки [8]. В простейшей модели предполагается, что скорость роста числа публикаций пропорциональна их достигнутому числу:

где у - число публикаций; k - константа. Решениями уравнения являются функции типа е^t, т.е. с увеличением времени t число публикаций растет экспоненциально.

Так как при t →∞ функция y(t) = е^t принимает бесконечно большие значения, модель (12.13) справедлива только на ограниченном временном интервале. Ясно, что при некотором t = t* механизм роста числа публикаций должен измениться. Для любого научного направления наступает этап насыщения (торможения).

Рассмотрим уравнение

где k и b - константы. Когда у увеличивается и становится сравнимым по величине с b, то (b-у) → 0 и, следовательно, dy/dt → 0, т.е. рост у прекращается.

Отметим, что данное логистическое уравнение является нелинейным, так как его правая часть содержит у².

В приведенных примерах динамическая модель описывается одним дифференциальным уравнением. Значительно более реалистические модели можно получить, рассматривая совокупность уравнений.

Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и

234

их производные. Решением системы дифференциальных уравнений называется совокупность функций y.(t) (i=l, ..., п), которые при подстановке в уравнения обращают их в тождества.

В данном учебном пособии рассматриваются системы дифференциальных уравнений, содержащие столько уравнений, сколько в них входит неизвестных функций, при этом все они являются функцией одной независимой переменной t.

Рассмотрим систему дифференциальных уравнений следующего вида:

Отметим, что в правых частях уравнений переменная t в явном виде не содержится. Такие системы называются автономными динамическими системами второго порядка. Основная геометрическая интерпретация системы (12.15) связана с рассмотрением плоскости (х, у), называемой фазовой плоскостью, и существенно отличается от геометрической интерпретации, описанной выше. Ее можно назвать кинематической, так как в этой интерпретации каждому решению ставится в соответствие движение точки по кривой, а не кривая в пространстве.

Системы типа (12.15) используются для описания эволюционных процессов. Точка фазового пространства определяет состояние системы. Приложенный к этой точке вектор с координатами dx/dt, dy/dt задает скорость изменения состояния. Точка, где этот вектор обращается в нуль, т.е. dx/dt = dy/dt = Q, называется положением равновесия, или особой точкой системы.

Решения системы (12.15) будем изображать параметрическими кривыми на фазовой плоскости (х, у): х = φ(t), y = Ψ(t). Сопоставим геометрическую интерпретацию системы (12.15) в пространстве (x,y,t) с интерпретацией на фазовой плоскости.

1. В каждую траекторию фазовой плоскости проектируется совокупность интегральных кривых в пространстве (х, у, t). Эти кривые получаются друг из друга заменой t на t-C, где С - произвольная константа (рис. 12.4, а).
2. Если точка (а, b) является состоянием равновесия системы (12.15) Р(а, b) = 0; Q(a, b) = 0, то интегральная кривая будет прямой, параллельной оси t. Эта прямая проектируется на плоскость (х, у) в единственную точку (a, b).
3. Если система имеет периодическое решение с периодом ос, то в пространстве (х, у, t) соответствующая интегральная кривая представляет собой спираль с шагом α. Эта спираль проектируется на фазовую плоскость в замкнутую кривую (рис. 12.4, б).

235

Рис. 12.4, Поведение решений в пространстве (х, у, t) и на фазовой плоскости

При проекции спирали на плоскость (х, t) или (у, t) получим синусоидальную кривую, которая показывает изменение переменной x(t) или y(t).

Системы дифференциальных уравнений часто используются для описания работы технических устройств (механических, электрических и т.д.). Так как система дифференциальных уравнений имеет бесконечное множество решений (конкретное решение определяется начальными условиями), то и технические устройства (машины, механизмы) могут иметь бесконечное множество режимов. На практике эти устройства работают во вполне определенных режимах, что может объясняться выбором конкретных начальных условий и тем, что устройство само стабилизует свою работу.

Рассмотрим хрестоматийный пример стенных часов с маятником. Если маятник отклонить от вертикального положения достаточно сильно, то часы будут идти с определенной амплитудой колебаний очень долго. Если маятник отклонить недостаточно сильно, то после небольшого числа колебаний он остановится. Таким образом, у данной динамической системы существуют два стационарных решения: периодическое решение, соответствующее нормальному ходу часов, и состояние равновесия - скорость маятника равна нулю. Всякое другое из бесконечного множества решений быстро приближается к одному из двух стационарных решений, каждое из которых является устойчивым в том смысле, что решение, не слишком сильно отклоняющееся

236

от стационарного в начальный момент, стремится к стационарному.

В окрестности особых точек фазовые траектории могут быть шести типов, схематично показанных на рис. 12.5 (стрелки на фазовой траектории указывают направление изменения параметра t).

На рис. 12.5 особая точка условно помещена в начало координат. Траектории, которым принадлежит особая точка на рис. 12.5,5, называются сепаратрисами.

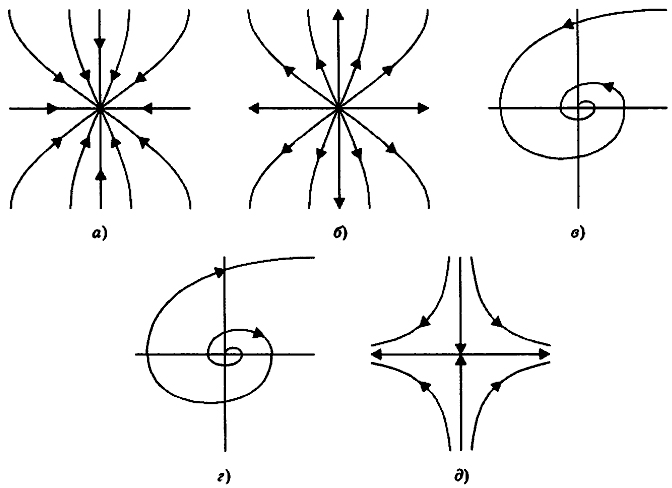
Рис. 12.5. Фазовые траектории в окрестности особой точки:
а - устойчивый узел; б - неустойчивый узел; в - устойчивый фокус; г - неустойчивый фокус; д - "седло"

Классификация типов поведения фазовых кривых в окрестности особой точки была осуществлена великим французским математиком и философом Анри Пуанкаре (1854-1912), который ввел также понятие предельного цикла, играющее важнейшую роль в различных приложениях теории дифференциальных уравнений.

Предельным циклом дифференциального уравнения называется изолированное периодическое решение этого уравнения (рис. 12.6). Для качественного исследования поведения динамической системы достаточно определить состояния равновесия, наличие предельных циклов, ход сепаратрис. С точки зрения

237

Рис. 12.6. Предельный цикл

качественного исследования знание точной формы траекторий не представляет интереса.

В настоящее время качественное изучение моделей эволюционных процессов стало доступно широкому кругу пользователей благодаря наличию и стремительному совершенствованию соответствующего программного обеспечения (пакеты прикладных программ DYANA, STELLA, Mathcad, Mathlab, Mathematica и др.). Не составляет труда получить достаточно точное решение дифференциального уравнения с помощью Excel [6].

Вместо решения дифференциального уравнения можно исследовать его аналог - разностное уравнение. Последнее можно считать приближенной моделью дифференциального уравнения. Следует иметь в виду, что решения разностного уравнения часто ведут себя менее гладко, чем решения дифференциального уравнения. В разностной модели учитывается поведение системы только на концах дискретных временных интервалов, тогда как дифференциальное уравнение описывает непрерывное течение процесса при каждом t.

При моделировании социальных процессов считается, что разностные уравнения более точно описывают процессы, связанные с электоральным циклом [23]. Действительно, возвращаясь к модели мобилизации из § 12.2, заметим, что процесс мобилизации можно считать дискретным, так как его действие проявляется в основном в период выборов.

Как будет показано в следующем параграфе, в простых случаях качественный анализ поведения системы может быть проделан без использования ЭВМ.

238