12.2. Приложения теории разностных уравнений к моделям
мобилизации

В теории разностных уравнений предполагается, что переменные исследуемого процесса определены в дискретные моменты t₁, t_z, ..., t_n. Интервал времени Δt = t_i+l - t., как правило, предполагается постоянным для любого i (i = 1,..., n,...). Целесообразность такого рассмотрения определяется исходными данными о социальном процессе, которые часто измеряются в дискретные моменты времени (официальная статистика, периодические опросы, переписи и т.д.). Интервал времени может равняться пятилетке, году, кварталу, месяцу, неделе и т.д. Если интервал становится бесконечно малым (Δt → 0), то процесс рассматривается как непрерывный и изучается с помощью теории дифференциальных уравнений.

Модель мобилизации. Под термином "политическая" или "социальная мобилизация" понимается вовлечение людей в партию или в число ее сторонников, обращение в какую-либо веру, участие в данном движении (борьба за мир, экология, здоровье и т.д.). Текущий уровень мобилизации тесно связан с прошлым уровнем, а будущая мобилизация зависит от сегодняшних успехов пропагандистской кампании. Используя простейшую динамическую модель, попытаемся отразить логику изменений уровня мобилизации между двумя соседними моментами времени [23].

Обозначим через М_t долю мобилизованного населения в момент t, тогда доля немобилизованного населения равна 1 - М_t. Пусть ΔМ_t обозначает изменение уровня мобилизации за единицу времени (год, месяц и т.д.):

ΔM_t = M_t+1 - M_t.

За время от t до t + 1 уровень мобилизации может измениться по двум причинам: 1) удалось дополнительно сагитировать часть населения g (1 - М_t), где g - коэффициент агитируемости, константа, не зависящая от времени; 2) часть населения, выбывающая из числа членов, участников, сторонников, равна fМ_t, где f - постоянный коэффициент выбытия (g ≥ 0, f ≥ 0). Параметры g и f выражают пропорции, в которых соответствующие части населения меняют свое поведения на рассматриваемом отрезке времени.

Тогда уравнение процесса мобилизации можно записать следующим образом:

229

Уравнение (12.5) может быть преобразовано следующим образом:

т.е. приведено к виду

который является стандартной формой линейного разностного уравнения первого порядка с постоянными коэффициентами.

Решением уравнения (12.7) называется такая функция M(t), что последовательность М_t удовлетворяет этому уравнению для заданной области значений t.

Уравнение (12.7) является простейшим и легко может быть решено алгебраическими методами. В общем случае решение данного уравнения имеет вид

M_t = ta₀ + M₀ для а₁ = 1.

Таким образом, решение уравнения (12.7) однозначно определяется начальным значением M₀.

Равновесие и устойчивость. Одно из присущих человеку качеств - стремление к стабильности - формализуется в теории динамических систем с помощью понятия равновесия.

Равновесие - состояние системы, в котором интересующие исследователя параметры остаются неизменными: М_t+1 = M_t, причем это не означает, что жизнь в системе вообще замирает. В рамках модели мобилизации предположение о постоянстве М_t не свидетельствует об отсутствия изменений среди сторонников данной партии (часть уезжает, умирает, других партии удается привлечь на свою сторону), но общее соотношение остается примерно постоянным.

Для определения точки равновесия системы М* подставим условие М_t+1 = М_t в уравнение (12.5), в результате чего получим

230

Следовательно,

М* +g / (1 + a₁).

Легко показать, что для уравнения (12.7) состояние равновесия вычисляется следующим образом:

Из соотношения (12.8) можно установить, что существуют только варианты поведения решения, изображенные на рис. 12.1 [23]. Вариант I описывает монотонную сходимость к состоянию равновесия (при a₁ > 0 и | a_l | < 1); вариант II - осциллирующую сходимость к состоянию равновесия (при а₁ < 0 и | а₁ | < 1); вариант III - монотонную расходимость (при a₁ > 0 и | a_l | > 1); вариант IV - осциллирующую расходимость (при а₁ < 0 и | a₁ |> 1).

Рис. 12.1. Качественное поведение решений уравнения (12.7)

По определению, варианты I и II характеризуют устойчивую систему - все решения сходятся к положению равновесия независимо

231

от значений М₀ и a₀, а варианты III и IV - неустойчивую систему.

Оценка параметров динамической модели. Модель мобилизации использовалась для изучения динамики числа голосов, поданных за демократическую партию США в Лэйк Кантри (штат Индиана) в период 1920-1968 гг. [23].

Для оценки численных значений коэффициентов а₀, а₁ модели применялся метод наименьших квадратов. Разностное уравнение (12.7) рассматривалось как линейное регрессионное уравнение у = т₀ + т₁ х, где у = М_t+1 - доля избирателей в Лэйк Кантри, голосующих за кандидатов от демократической партии в год t + 1 = 1924, 1928,..., 1968; х = M_t - доля голосующих за демократов в год t = 1920, 1924,..., 1964.

С помощью метода наименьших квадратов в [23] получены следующие значения коэффициентов: т₀ = 0,14; т₁ = 0,62. По формуле (12.10) вычисляем состояние равновесия:

Mˆ =

m0ˆ	=	1 - m1ˆ
0,14		1 - 0,62

 = 0,37

На рис. 12.2,а изображен график наблюдаемых значений M_t, а на рис. 12.2,б - график решения разностного уравнения (12.7) при М₀ = М₁₉₂₀.

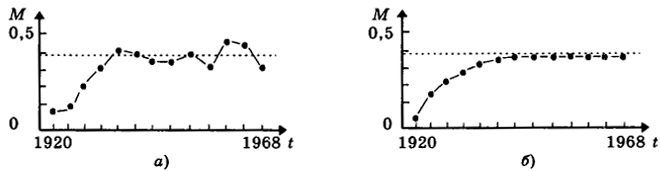
Рис. 12.2. Динамика голосующих за демократов на президентских выборах в Лэйк Кантри (1920-1968)

Сравнение графиков на рис. 12.2, а и б показывает, что разностное уравнение достаточно хорошо описывает качественные характеристики процесса мобилизации. Ясно, что данная модель является чрезвычайно упрощенной, реалистические модели требуют учета большого числа факторов и нелинейных соотношений, однако для понимания поведения систем иногда достаточно изучить простые варианты модели.

232