11.3. Диссипативные структуры И. Пригожина

В теории диссипативных структур, развиваемой И. Пригожиным и его школой, первоначально изучались процессы самоорганизации в физико-химических системах [18-20]. До работ Пригожина в естествознании в основном изучались равновесные структуры, которые можно рассматривать как результат статистической компенсации активности микроскопических элементов (молекул, атомов).

Если систему с равновесной структурой изолировать от внешней среды, то ввиду инертности данная равновесная структура может существовать бесконечно долго. Однако в биологических и социальных системах ситуация, как правило, другая: система незамкнута, открыта и, более того, существует потому, что она открыта, питается потоками вещества, энергии, информации, поступающими из внешнего мира. В открытых системах случайные флуктуации "пытаются" вывести систему из равновесного состояния. В реальных системах незначительные флуктуации, как правило, подавляются, и система остается стабильной. Если же силы, действующие на систему, становятся достаточно большими и вынуждают ее достаточно далеко уйти от положения равновесия, то состояние системы становится неустойчивым. Некоторые флуктуации могут не затухать, а усиливаться и завладевать всей системой. В результате действия положительной обратной связи флуктуации усиливаются и могут привести к разрушению существующей структуры и переходу в новое состояние. Причем возможен переход и на более высокий уровень упорядоченности, называемый диссипативной структурой. Возникает явление самоорганизации.

Исследуя динамику сильно неравновесных систем, И. Пригожий приходит к следующим выводам: "Когда система, эволюционируя, достигает точки бифуркации, детерминистическое описание становится непригодным. Флуктуация вынуждает систему выбрать ту ветвь, по которой будет происходить дальнейшая эволюция системы. Переход через бифуркацию - такой же случайный процесс, как бросание монеты. Существование неустойчивости можно рассматривать как результат флуктуации, которая сначала была локализована в малой части системы, а затем распространилась

214

и привела к новому макроскопическому состоянию" [20, с. 56].

Известный американский футуролог О. Тоффлер в предисловии к [20] отмечает, что "пригожинская парадигма особенно интересна тем, что она акцентирует внимание на аспектах реальности, наиболее характерных для современной стадии ускоренных социальных изменений: разупорядоченности, неустойчивости, разнообразии, неравновесности, нелинейных соотношениях, в которых малый сигнал на входе может вызвать сколь угодно сильный отклик на выходе, и темпоральности - повышенной чувствительности к ходу времени" [20, с. 16-17].

Принципы, разработанные Пригожиным для анализа химических процессов, были распространены на широкий класс явлений в физике, молекулярной биологии, процессов эволюции в биологии, а затем и социологии. Так, в [20, с. 246] описан процесс самоорганизации у термитов - построение термитника. Предполагается, что первая стадия - основание термитника - является результатом беспорядочного поведения термитов. Термиты приносят и беспорядочно разбрасывают комочки земли. Каждый комочек пропитывается гормоном, привлекающим других термитов. Случайным образом в этом процессе возникает флуктуация - несколько большая концентрация комочков земли в окрестности некоторой точки. Повышенная концентрация гормонов привлекает к этой точке большее число термитов. Процесс концентрации термитов усиливается благодаря положительной обратной связи. Постепенно возникают "опоры" термитника.

Процесс построения термитника - яркий пример явления самоорганизации, возникновения сложной структуры в хаотической среде благодаря флуктуации. В настоящее время в естественных науках ведется активное исследование явлений, связанных с возникновением структур, самоорганизацией в простейших нелинейных средах. Делаются попытки выявить прообразы появления организации и в более сложных, в частности социальных, системах. Ученые ведут исследования простейших моделей, анализ которых не может заменить изучение сложных социальных процессов, но может дать исследователям полезную подсказку, помочь подметить скрытые закономерности, сформулировать плодотворные гипотезы.

В работе И. Пригожина и И. Стенгерс [20] рассматривается понятие логистической эволюции, т.е. процессов, описываемых логистическим уравнением (см. § 9.2). Исследуется модель эволюции популяций из N особей. Пусть r и т - коэффициенты

215

рождаемости и смертности, К - "несущая способность" окружающей среды. Тогда процесс эволюции популяции может быть описан следующим уравнением:

dN / dt = r · N(K - N) - m · N.

Система имеет устойчивое стационарное состояние N_c =К - т/r. При любом начальном значении N₀ численность популяции стремится к значению N_c, которое зависит от разности между несущей способностью среды и отношением коэффициентов смертности и рождаемости. В стационарном состоянии в каждый момент рождается столько индивидов, сколько их погибает.

Ясно, что в процессе эволюции параметры К, т, r могут изменяться (например, под влиянием климатических флуктуации). Живые сообщества пытаются увеличить параметр К, изыскивая новые способы эксплуатации природных ресурсов. Инстинкт жизни обусловливает стремление к увеличению рождаемости и снижению смертности. "Каждое экологическое равновесие, определяемое логистическим уравнением, носит лишь временный характер, и логистически заданная экологическая ниша последовательно заполняется серией видов, каждый из которых вытесняет предшествующие, когда его "способность" к использованию ниши, измеряемая величиной К - т/r, становится больше, чем у них" [20, с. 255]. На рис. 11.8 показана временная эволюция популяции X, состоящей из последовательности видов x1, x2, х3. Каждому новому виду соответствует возрастающее значение К- т/r.

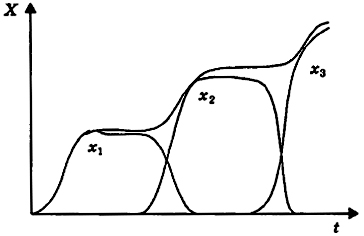
Рис. 11.8. Эволюция популяции X

Как указывается в [20], логистическое уравнение позволяет количественно сформулировать дарвиновскую идею о выживании наиболее приспособленного в предположении, что наиболее приспособленным является вид с наибольшим значением (К - т/r). Подобным образом могут быть объяснены процессы эволюции социума, связанные с внедрением технологических инноваций.

Логистическая модель эволюции в настоящее время исследуется в различных областях науки. Аналогичная модель использовалась для анализа смены технологических укладов (см. § 7.1).

216

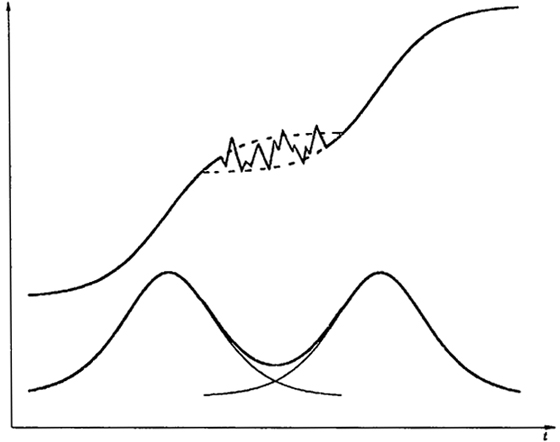
Рис. 11.9. Хаос в эволюции

Оказалось, что в моделях этого типа также возможны хаотические состояния. На рис. 11.9 показан пример траектории логистической эволюции.

Как утверждается в [27], хаотические колебания могут возникнуть в период замены старого уклада на новый. Возникновение нестабильности может интерпретироваться как случайный поиск равновесного состояния системой, оказавшейся в ситуации, когда растущие возможности не могут быть реализованы в рамках существующей ниши. Данная модель демонстрирует чередование режимов порядка и хаоса. В период быстрого экономического роста многие компании консолидируются, интегрируются. Корпорации работают как часы, подчиняясь эффективному централизованному управлению. В стадии насыщения под давлением инноваций экономическая система попадает в полосу хаоса.

Авторы [20] полагают, что модели, построенные на основе понятия "порядок через флуктуации", будут способствовать более точной формулировке "сложного взаимодействия между индивидуальным и коллективным аспектами поведения". Модели такого типа "открывают перед нами неустойчивый мир, в котором малые причины порождают большие следствия, но мир этот не произволен. Напротив, причины усиления малых событий - вполне

217

"законный" предмет рационального анализа... Если флуктуация становится неуправляемой, это еще не означает, что мы не можем локализовать причины неустойчивости, вызванные усилением флуктуации" [20, с. 270].

В состоянии хаоса поведение системы непредсказуемо. Точнее, нельзя предсказать конкретное состояние, проследить заданную траекторию на длительном временном интервале. Однако вероятностные, усредненные характеристики могут быть спрогнозированы [12].

В качестве примера рассмотрим наклонный желоб, по которому течет вода. Если бросить в него разноцветные песчинки, то они стройными рядами поплывут вниз. Попробуем положить в желоб несколько камней. Спокойное течение сменится турбулентным. Траектории песчинок, определяемые завихрениями и водоворотами, станут трудно прогнозируемыми. Две в начале близкие песчинки к концу пути могут оказаться далеко друг от друга. Однако интегральные характеристики системы (например, количество жидкости, вытекающей из желоба в единицу времени) могут вести себя достаточно устойчиво.

Странный аттрактор, определяющий хаотическое поведение системы, часто занимает ограниченную область фазового пространства. Поэтому, хотя траектории разбегаются с экспоненциальной скоростью, убежать за границы странного аттрактора они не могут. Следовательно, определение границ области хаоса может позволить получить оценки поведения системы. Можно ли управлять подобными системами? Не только можно, но и нужно. Чувствительность такой системы позволяет вывести ее из хаотического состояния с помощью очень малых, но точных и своевременных воздействий [16].

Обязана ли социальная система притягиваться к странному аттрактору? Нет. Управляющие воздействия, введение дополнительных ограничений могут позволить избежать хаотических состояний.

Отметим, что далеко не все теоретики считают, что хаоса следует избегать. Верящие в животворную силу хаоса, наоборот, полагают, что чем он окажется обширнее, глубже, тем более эффективный порядок смогут породить творческие силы самоорганизации.

♦ ♦ ♦

Нельзя не согласится с доктором философских наук В.П. Бранским, заметившим, что "хотя синергетический подход к социальным явлениям завоевал в последней четверти XX века широкую

218

популярность, тем не менее пока он во многих случаях не выходит за рамки философской публицистики" [3, с. 148]¹.

Конечно, знание основных концепций синергетики необходимо современному специалисту, но для практических целей полезней не углубление философской рефлексии, а развитие нелинейной интуиции.

В данном пособии предлагается достаточно прагматичный подход к освоению хаоса. Читателю рекомендуется завести странный аттрактор не в голове, а в компьютере. Моделирование нелинейного поведения систем на ЭВМ не требует знания прикладной математики и вполне доступно студентам-социологам (см. § 13.2).

Задачи и упражнения

1. Катастрофа - это скачкообразный переход системы в лучшее или худшее состояние?
2. Ряд авторов полагает, что система в точке бифуркации выбирает тот или иной вариант дальнейшего развития с равной вероятностью. Верно ли это утверждение для социальных систем?
3. Можно ли использовать модель катастрофы "сборка" для описания политических революций? Попытайтесь построить такую модель на базе модели Т. Скокпол (см. § 10.3). Учтите, что в ее модели три независимых фактора, поэтому одним фактором придется пожертвовать.
4. Что преобладает в вашей жизни: хаос или порядок?
5. Какие процессы преобладают в вашей жизни: организации или самоорганизации?
6. Приведите примеры процессов самоорганизации из студенческой жизни.
7. Являются ли специалистами по синергетике сторонники лозунга "Анархия мать порядка"?
8. Какие процессы в экономике можно считать хаотическими?
9. Могут ли концепции синергетики оказаться полезными для планирования предвыборной кампании?
10. Можно ли спрогнозировать исход выборов за неделю, месяц, год и пять лет до начала голосования?
11. Верно ли утверждение, что в сфере искусства процессы самоорганизации играют главную роль?

219

Литература

1. Арнольд В.И. Теория катастроф. М., 1990.
2. Базыкин А.Д., Кузнецов Ю.А., Хибник А.И. Портреты 61 бифуркаций: Бифуркационные диаграммы динамических систем на плоскости // Новое в жизни, науке, технике. Сер. "Математика, кибернетика". 1989. №3.
3. Бранский В.П. Теоретические основания социальной синергетики // Петербургская социология. 1997. № 1. С. 148-179.
4. Давыдов А.А., Чураков А.Н. Модульный анализ и моделирование социума. М., 2000.
5. Евин И.А. Синергетика искусства. М., 1993.
6. Иваницкий Г.Р. На пути к второй интеллектуальной революции // Техника кино и телевидения. 1988. № 5. С. 33-40.
7. Иваницкий Г.Р. Синергетика // Новое в жизни, науке и технике. Сер. "Математика, кибернетика". 1989. № 7.
8. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. М.: Наука, 1994.
9. Концепция самоорганизации в исторической перспективе. М.: Наука, 1994.
10. Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. М.: Наука, 1990.
11. Лотман Ю. Клио на распутье // Наше наследие. 1988. № 5. С. 1-4.
12. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент: Введение в нелинейную динамику. М.: Наука, 1997.
13. Митина О.В., Петренко В.Ф. Динамика политического сознания как процесс самоорганизации // Общественные науки и современность. 1995. №5. С. 103-115.
14. Моисеев Н.Н. Алгоритмы развития. М., 1987.
15. Назаретян А.П. Агрессия, мораль и кризисы в развитии мировой культуры. М., 1996.
16. Новое в синергетике. Загадки мира неравновесных структур. М.: Наука, 1996.
17. Постов Т., Стюарт И. Теория катастроф и ее приложения. М., 1980.
18. Пригожий И. От существующего к возникающему. М., 1985.
19. Пригожий И., Стенгерс И. Время. Хаос. Квант. М.: Прогресс, 1994.
20. Пригожий И., Стенгерс И. Порядок из хаоса: Новый диалог с природой. М., 1986.
21. Синергетическая парадигма. Многообразие поисков и подходов. М., 2000.
22. Хакен Г. Синергетика. М., 1985.
23. Baumol W.J., Benhabib J. Chaos: Significance, Mechanism, and Economic Applications // J. of Economic Perspective. 1989. Vol. 3. № 1. P. 77-105.

220

24. Casti J.L. Searching for Certainty. N.Y.: W.Morrow, 1990.
25. Chaos Theory in the Social Sciences /Eds. L.D.Kiel, E.Elliot. Ann Arbor: The Univ. of Michigan Press, 1996.
26. Davidov A.A. Intermedity-Basic State of Social Systems? // Systems Research. 1993. Vol. 10. № 4. P. 81-84.
27. Modis T. Fractal Aspects of Natural Growth // Technological Forecasting and Social Change. 1994. Vol. 47. № 1. P. 63-73.
28. Oliva T.A. Information and Probability Estimates: Modelling the Firm's Decision to Adopt a New Technology // Management Science. 1991. Vol. 37. № 5. P. 607-623.
29. Zeeman E.G. et al. A model for institutional disturbances // Br. Math. Statist. Phsych. 1976. Vol. 29. P. 66-90.

221