9.2. Модели диффузии инноваций и логистического роста

Методы диффузии инноваций могут быть распространены и на изучение динамики антисоциального поведения - форм коллективного протеста, тактики террористов, распространения наркотиков и т.д. Антисоциальные движения нередко возникают как оппозиция происходящим переменам, вызванным какой-либо инновацией. В качестве примера обычно приводят движение луддистов, которые между 1811 и 1816 гг. разбили немало текстильных машин, что лишь ненадолго замедлило развитие английской легкой промышленности. Менее известно аналогичное движение под руководством капитана Свинга, пытавшегося теми же методами остановить процесс распространения сельскохозяйственной техники (механических молотилок). На рис. 9.1 представлены

Рис. 9.1. Динамика движения протеста в Англии в 1830 г. [14]

184

данные о динамике этого процесса, протекавшего всего месяц - с 8 ноября по 8 декабря 1830 г.

Точки на графике показывают, сколько машин было разрушено в данный день плюс число машин, уже сломанных к этому времени. Удивительно, что львиная доля машин была уничтожена всего за десять дней (с 18 по 28 ноября), что говорит о высокой эффективности социальных сетей коммуникаций - ведь в те времена в сельской Англии не было современного транспорта и средств связи [14].

Стоит обратить внимание на то, насколько хорошо логистическая кривая (показана сплошной линией) описывает динамику стихийного протеста. Эмпирический анализ огромного числа природных, технико-экономических и социокультурных процессов показал, что динамика процессов их роста, развития, распространения подчиняется логистическому закону. На рис. 9.2 приведена динамика развития сетей транспорта и коммуникаций в США, подчиняющаяся логистическим закономерностям.

Рис. 9.2. Динамика развития инфраструктуры США [14]

Для того чтобы понять сущность механизма, формирующего логистическую кривую, необходимо построить содержательные и формальные модели исследуемых процессов. Начнем с более простого случая - модели неограниченного экспоненционального роста.

Модель экспоненциального роста численности популяции. Обозначим через y_t численность популяции к моменту времени t. Если измерять значение y_t только в дискретные моменты времени (например, раз в год), то прирост численности популяции в год равен (y_t - y_{t - 1}). Если считать, что условия благоприятны для

185

развития популяции, - ресурсы неограничены, враги отсутствуют, то можно предположить, что прирост численности популяции пропорционален достигнутой численности. Это содержательное предположение может быть формализовано в виде следующего уравнения:

где a - коэффициент пропорциональности. Такие уравнения называются разностными.

Покажем, каким образом формируется механизм экспоненциального роста. Действительно, уравнение (9.1) легко преобразуется к уравнению

из которого видно, что каждое последующее значение y_t умножается на фиксированную константу (1 + а). Таким образом, значения y_t являются геометрической прогрессией и, следовательно, y(t) растет экспоненциально (как функция е^t).

О геометрической прогрессии как о законе роста населения писал Т. Мальтус (1766-1834). Используя его модель, Ч.Дарвин рассчитывал потенциальные возможности роста разных популяций. Согласно его расчетам, число потомков одной пары слонов через 750 лет может достичь 19 млн.

Значительно быстрее размножаются бактерии. Если одна бактерия в благоприятной среде делится каждые 20 мин., то при сохранении таких темпов деления потомство этой бактерии всего за 36 ч сможет образовать массу, которая покроет земной шар сплошным слоем толщиной 30 см, а еще через 2 ч толщина этого слоя достигнет 2 м [3].

Ясно, что процессы экспоненциального роста не могут длиться долго. Но на коротком временном интервале процессы роста могут быть описаны экспоненциальной кривой. Так, в 1937 г. на небольшой остров у побережья США завезли 8 фазанов, а через 6 лет популяция насчитывала уже 1898 птиц. Первые четыре года рост численности фазанов хорошо описывался экспоненциальной зависимостью. К сожалению, в начале войны на острове были размещены войска, ежегодный учет прекратился, а фазанов съели [3].

Модели логистического роста. Известно, что многие процессы в природе и обществе имеют пределы возможных изменений, в первую очередь из-за ограниченности ресурсов. Возвращаясь к диффузии инноваций, естественно предположить, что распространение нововведений ограничено емкостью данного сегмента рынка,

186

возможностями целевой группы. Одним из главных факторов, определяющих скорость процессов диффузии, является межличностное общение между сторонниками данной новинки и теми, кто еще колеблется или вообще ничего не слышал о предлагаемом нововведении. Если обозначить число людей, принявших инновацию к моменту t, через y_t , то число лиц, которых, в принципе, можно еще сагитировать, составит М - y_t, где М - емкость рынка, максимально возможное число лиц, способных адаптировать данное нововведение. Можно считать, что прирост числа сторонников новинки пропорционален числу встреч между сторонниками новинки и сомневающимися. Число таких встреч пропорционально произведению y_t (М - y_t)¹.

Формализация этих содержательных предположений приводит к следующему разностному уравнению:

где а - коэффициент пропорциональности.

Решением этого уравнения является логистическая функция, а само уравнение называется логистическим (более подробно технические детали описаны в § 12.1). Впервые логистическая модель как модель роста народонаселения была предложена бельгийским математиком П.Ф. Ферхюльстом в 1838 г. В теории инноваций логистическую модель иногда называют моделью Фишера-Прея.

Логистическую S-образную кривую иногда называют кривой Перла - по имени американского демографа Р. Перла (1870-1940), который провел огромное число эмпирических исследований роста различных организмов и популяций. Он обнаружил, что по логистическому закону увеличивается вес тыквы, растет число дрожжевых бактерий, росло народонаселение США до 1940 г. Позже выяснилось, что S-образные кривые хорошо описывают процессы замещения одной техники другой, смену технологий, эволюционные процессы в экономической и социокультурной сферах.

Биологи дают логистическому уравнению несколько иную содержательную интерпретацию. Если в правой части уравнения (9.3) раскрыть скобки, то получим

187

Первое слагаемое правой части уравнения означает, что прирост численности популяции пропорционален достигнутой численности. Второй член (- a y_{t - 1}²) формализует утверждение - прирост обратно пропорционален квадрату численности популяции. Биологи приводят следующие доводы в пользу данного предположения: чем больше число встреч между особями, чем выше плотность популяции, тем выше вероятность заболеваний, конфликтов, иначе говоря, выше "сопротивление среды", а значит, меньше прирост численности популяции¹.

Попробуем проанализировать действие логистического механизма с помощью петель обратной связи.

Как видно из рис. 9.3, данная причинно-следственная модель имеет две петли обратной связи. Действие расположенной справа петли положительной обратной связи постепенно ведет к экспоненциальному росту численности популяции. Слева на рис. 9.3 изображена петля отрицательной обратной связи, действие которой призвано стабилизировать процесс на уровне насыщения. Результирующая динамика процесса определяется поочередным доминированием петель. Сначала, пока процесс не дойдет до середины (М/2), доминирует петля положительной обратной связи.

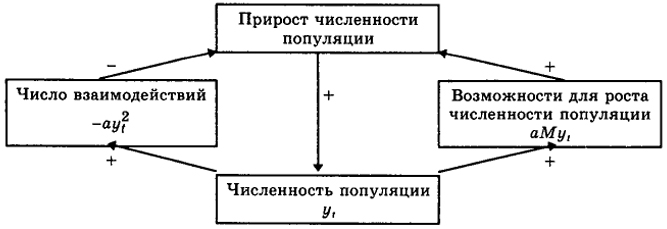
Рис. 9.3. Диаграмма логистического уравнения

188

После прохождения центра симметрии доминирующее влияние оказывает петля отрицательной обратной связи [17].

Конечно, приведенные утверждения нельзя назвать совершенно очевидными. Более подробное изложение возможностей качественного анализа поведения систем с помощью петель обратной связи дается в разд. 3.

Чтобы у читателя не сложилось впечатление, что все процессы роста описываются логистическим уравнением, рассмотрим кривую Гомперца, названную в честь английского статистика и математика XIX века. Б. Гомперц, исследуя уровни смертности, распределение доходов и др., установил, что в ряде случаев их динамика описывается кривой у = а^bt , где коэффициенты а и b удовлетворяют условиям: 0<а<1, b < 1.

Кривые Перла и Гомперца относятся к классу S-образных кривых, отображающих динамику роста кумулятивного значения показателя, например числа продаж новинки (рис. 9.4). Чтобы перейти к более привычной форме визуализации данных, надо взять производную от S-образной функции. При этом получим кол околообразную функцию, отображающую число продаж в данный момент времени (рис. 9.5). Можно ли сказать, что на рис. 9.5 представлена модель жизненного цикла инновации? Да. Но только в том случае, если товар покупается один раз и время его использования мало. Если же продукт потребляется многократно, то его жизненный цикл выглядит сложнее (рис. 9.6).

Спад в числе продаж связан с тем, что ряд потребителей, купив новинку один раз, не становятся ее поклонниками. После пика уровень продаж товара стабилизируется. Остаются только постоянные покупатели. В завершающий же фазе жизненного

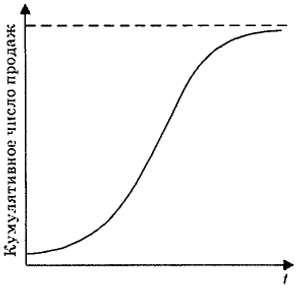
Рис. 9.5. Динамика числа продаж

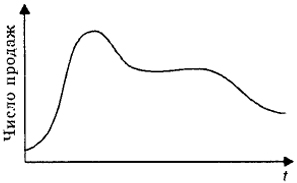
Рис. 9.4. Динамика кумулятивного числа продаж новинки

189

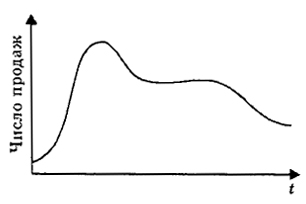
Рис. 9.6. Жизненный цикл новинки

цикла данный продукт будет вытеснен с рынка новым, более предпочтительным товаром [15].

В заключение приведем любопытный пример прогнозирования процесса демократизации. В 1991 г. Дж. Модельски и Г. Перри преддожили рассмотреть процесс распространения демократической формы правления как процесс диффузии инновации. По мнению американских политологов, демократия начала распространяться по земному шару в XV веке. Первая фаза распространения демократических форм правления - авторы назвали ее экспериментальной - длилась с 1450 по 1800 г. В это время доля населения, опробовавшая демократические процедуры, не превышала 1-2% всего населения земли. Далее процесс диффузии начал набирать обороты. К 1990 г. уже 40% населения земли избрало демократические формы правления. По прогнозу авторов к концу XX столетия будет достигнута отметка 50%, а к 2100 г. уже 90% населения будут жить при наилучшей форме государственного устройства [16].

В своих расчетах авторы использовали для прогноза логистическую модель диффузии инноваций. Хотя содержательные предположения, лежащие в основе этой модели, не всегда бесспорны, число примеров ее успешного использования на практике огромно.

Задачи и упражнения

1. Приведите примеры социокультурных процессов, которые нельзя представить как диффузию нововведений.
2. Какие технические инновации будут оказывать наибольшее влияние на социум в ближайшем будущем?
3. Следует ли учитывать демографические изменения при анализе социокультурных нововведений?
4. Некоторые футурологи давно предрекают широкое распространение групповой формы семьи. Что, на ваш взгляд, сдерживает диффузию этого нововведения?
5. Постройте модель распространения нововведений в сфере образования.
6. Перечислите когнитивные факторы, влияющие на успех инновации.
7. Какие индикаторы сигнализируют о том, что социальная система жаждет перемен?

190

8. Всегда ли широкая рекламная кампания гарантирует успех новому товару?
9. Почему "дурные примеры" заразительны?

Литература

1. Академия рынка. Маркетинг. М.: Экономика, 1993.
2. Бестужев-Лада И.В. Прогнозное обоснование социальных нововведений. М.: Наука, 1993.
3. Гиляров A.M. Популяционная экология. М.: МГУ, 1990.
4. Глазьев С.Ю. Теория долгосрочного технико-экономического развития. М., 1993.
5. Друкер П.Ф. Рынок: как выйти в лидеры. Практика и принципы. М., 1992.
6. Брасов B.C. Социальная культурология. М.: Аспект Пресс, 1996.
7. Пригожий А.И. Современная социология организаций. М.: Интерпресс, 1995.
8. Смайлор Р.Н. и др. Предпринимательский университет // Международный журнал социальных наук. 1993. № 2. С. 3-17.
9. Bandura A. Social Foundation of Thought and Action. A Social Cognitive Theory. Stanfford Univ. New Jersey: Printice-Hall, 1986.
10. Bridges E. New technology adoption in an innovative marketplace // Inter. Journal of Forecasting. 1991. Vol. 7. № 2. P. 257-270.
11. Diffusion of Technologies and Social Behavior / Eds. N.Nakicenovic and A.Grubler. Berlin: Springer, 1991.
12. Grubler A. Time for a Change: On the Pattern of Diffusion of Innovation // Daedalus. 1996. № 1. P. 19-42.
13. Kotler F. Marketing Decision Making. A Model Building Approach. N.Y.: Holt., 1971.
14. Modelski G., Perry G. Democratization in Long Perspective // Technological Forecasting and Social Change. 1991. Vol. 39. № 1. P. 23-34.
15. Richardson G.P. System Dynamics: Simulation for Policy Analysis from a Feedback Perspective // Qualitative Simulation, Modeling and Analysis / Ed. P.A.Fishwick. N.Y.: Springer. 1991. P. 144-169.
16. Rogers E. Diffusion of Innovations. 3 ed. N.Y.: Free Press, 1983.
17. Schon D. Beyond the Stable State. N.Y.: Norton, 1971.

191