Социолог, наблюдая за интересующими его характеристиками конкретного социального процесса, может наглядно представить себе течение процесса в виде графика. Обычно в таких случаях используются двумерные графики, причем по оси абсцисс принято откладывать время, а по оси ординат значения переменной, характеристики, показателя, индикатора или фактора, описывающего поведение данной системы. На рис. 5.1 приведен пример линейной зависимости показателя S от времени t.
График, приведенный на рис. 5.1, демонстрирует траекторию L1 линейного, равномерного роста значения показателя S при увеличении времени t. Траектория прямой L2 отражает процесс
112

Рис. 5.1. Линейная траектория
равномерного уменьшения, снижения показателя S. Для простоты на последующих рисунках будем изображать только процессы роста, подразумевая, что траектории упадка могут быть легко построены по аналогии.
Понятно, что линейный рост или снижение значения какого-либо показателя не может длиться бесконечно. (Например, для многих индикаторов отрицательные значения не имеют смысла.) Отсюда следует, что за пределами рассматриваемого временного интервала ход процесса должен замедлиться или ускориться и траектория должна перестать быть линейной и приобрести более сложный, нелинейный характер. В линейных моделях скорость (темп изменений) остается постоянной величиной, тогда как скорость течения нелинейных процессов меняется.
Глубокий анализ социокультурных процессов предполагает изучение не только изменений абсолютных значений данного показателя, но и слежение за скоростью изменения. (Необходимо исследование не только функции S(t), но и ее производной.)
Мы неявно считали, что показатель S является количественной переменной, что совсем не обязательно. Многие переменные, характеризующие течение социальных процессов, являются качественными, но их траектории также могут быть изображены графически. Более того, многие количественные переменные имеют качественную составляющую. Даже данные официальной статистики могут содержать информацию, полученную на основе экспертных оценок.
Типичный график, отражающий чередование разных этапов, стадий, фаз развития социальной системы приведен на рис. 5.2.
Процессы роста в социокультурных системах не обязаны
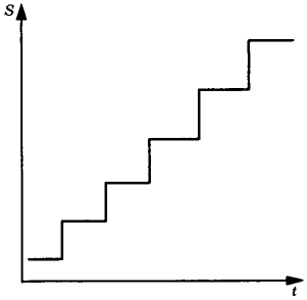
Рис. 5.2. Ступенчатая траектория развития
113
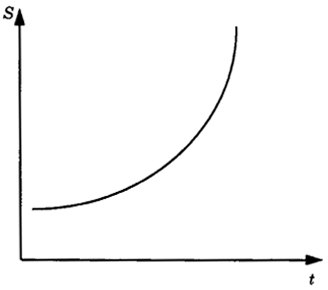
Рис. 5.3. Экспоненциальная зависимость
Рис. 5.4. Квадратичная зависимость
подчиняться только линейной зависимости. Траектория роста может описываться экспоненциальной кривой типа еt (рис. 5.3), квадратичной кривой (рис. 5.4). Значительно более медленный рост показателя S часто отражает логарифмическая траектория (рис. 5.5). Конечно, значение показателя не всегда монотонно возрастает. В ходе процесса возможен и кратковременный спад. На рис. 5.6 изображена кубическая модель подобной траектории (S(t) = a1t3 + a2t2 + a3t + a4).
Большинство реальных процессов не может расти до бесконечности. Ограниченность имеющихся ресурсов тормозит рост и не позволяет превзойти некоторые предельные значения. Наличие пределов роста или точек насыщения обычно описывается моделями двух типов:

Рис 5.5. Логарифмическая зависимость

Рис. 5.6. Кубическая зависимость
114
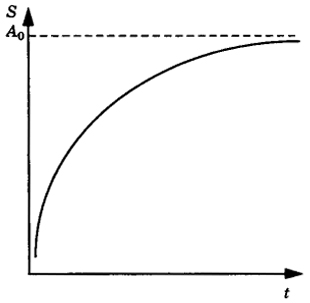
Рис. 5.7. Модель насыщения без точки перегиба

Рис. 5.8 Логистическая кривая
- а) насыщение без точек перегиба (рис. 5.7). Такие траектории может иметь функция типа S = A0 - E-T или S = A0 - 1/t (гипербола);
- б) насыщение с точкой перегиба (рис. 5.8). Кривая такого типа называется логистической или S-образной. Подобную траекторию имеет функция типа S = A0 / (1 + E-T). Как будет видно из дальнейшего изложения, ход многих социокультурных процессов хорошо описывается именно логистической кривой. Такие процессы сначала растут очень медленно. Затем рост ускоряется, например под действием контура положительной обратной связи. Но после прохождения точки перегиба темп роста начинает замедляться. Под действием контура отрицательной обратной связи процесс сначала замедляется, а затем стабилизируется, не переходя предельно возможное значение А0.
Как уже говорилось, наиболее популярной формой социокультурных процессов является прямая линия, отражающая линейные представления о ходе социального времени. Однако мыслителей всех времен привлекала также циклическая модель социального времени, предполагающая периодическое

Рис. 5.9. Циклическая модель с горизонтальным трендом
115
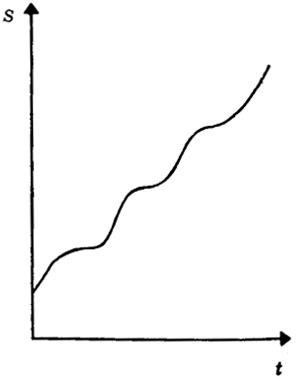
Рис. 5.10. Циклическая следовании синусоиде в случае
повторение определенных фаз развития, рекуррентное возвращение к исходному состоянию. Простейшая траектория циклического типа в виде синусоидальной кривой с горизонтальным трендом приведена на рис. 5.9, а с линейно возрастающим трендом - на рис. 5.10. Циклическая траектория количественной переменной не обязательно точно соответствует графику математической синусоиды - период и амплитуда колебаний могут со временем меняться.
Естественно, говорить о точном модель с восходящим трендом качественной переменной просто неуместно. Именно качественные переменные, как правило, имеют в виду, рассматривая развитие процесса по спирали. Известно, что образ спирали обладает большой генеративной силой, весьма способствует инсайту, благодаря чему довольно часто фигурирует в трудах обществоведов в качестве одной из базовых метафор социальных изменений. Как геометрический объект спираль изображается в трехмерном пространстве, одной координатой которого является время t, а две другие координаты соответствуют двум показателям S^ и S2, характеризующим эволюцию наблюдаемой системы V. Причем следует обязательно учитывать то, что спираль отражает динамику взаимодействия именно двух взаимосвязанных факторов.
Пример спирали М, приведенной на рис. 5. 11, показывает, что в простейшем случае спираль можно представить в виде линии, наматываемой на цилиндр (изображен штриховой линией). Ясно, что цилиндр не обязательно расположен горизонтально, он может быть и наклонен.
Чтобы более наглядно представить ход изменения значений факторов S1 и S2, спроектируем спираль сначала на плоскость (S1; t), a затем на плоскость (S2; t). Получим две траектории синусоидального типа F1 и F2. Если мы попробуем изобразить их на одном графике с общей осью времени, то сразу заметим, что фазы колебаний факторов S1 и S2 не совпадают (рис. 5.12). Чтобы наглядно представить себе взаимосвязь факторов S1 И S2, спроектируем спираль на плоскость (S1; S2). Очевидно, что в этом случае получим круг, изображенный на
116

Рис. 5.11. Простейшая спираль
рис. 5.13. На рисунке движение по спирали становится движением по кругу по часовой стрелке (в данном случае время t можно рассматривать как параметр1). Чередование фаз изменения факторов S: и S2 при движении по секторам АВ; ВС; CD; DA круга представлено в табл. 5.2.
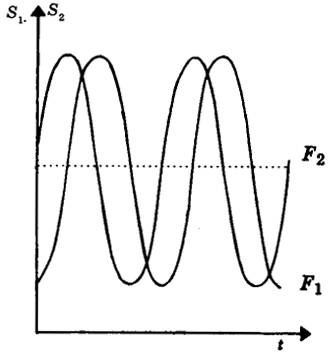
Рис. 5.12. Сдвиг фаз

Рис. 5.13. Состояния системы
117
Таблица 5.2. Чередование фаз
| Сектор |
Изменение фазы |
| |
S1 |
S2 |
| АВ |
+ |
+ |
| ВС |
+ |
- |
| CD |
- |
- |
| DA |
- |
+ |
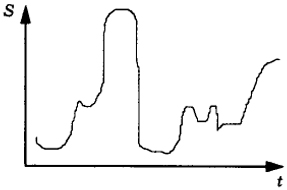
Рис. 5.14. Хаотический процесс
Как видим, в рассматриваемом случае чередование фаз развития системы в целом и отдельных ее показателей не является синхронным.
Еще сложнее анализировать динамику социокультурных процессов, имеющих хаотический характер. Пример такого процесса приведен на рис. 5.14. Динамика хаотических процессов чрезвычайно запутана и трудно прогнозируема. Медленный равномерный рост сменяют "большие скачки", амплитуда и период колебаний меняются самым причудливым образом. Для подобных процессов удается выявить только самые общие тенденции, как это и принято в глобальных теориях социальной эволюции.
118
1
Простейшая винтовая линия в пространстве может быть представлена в параметрическом виде:
х =
acos
t;
у =
asin
t;
z = ct.
