В металлургическом производстве большую роль играют процессы, в которых участвуют жидкие фазы: растворение скрапа в жидком чугуне; растворение извести или руды в жидком шлаке; растворение и выделение газов из жидкой стали; переход элементов из жидкого металла в шлак при процессах рафинирования.
485
Наиболее простым случаем является растворение твердых тел в жидкостях. На основании большого экспериментального материала А.Н. Щукарев в 1891 г. нашел общий закон, выражающий скорость этого процесса:
Q = k(cн - cо)S,
(XVIII.31)
где Q - количество вещества, растворяющегося в единицу времени; S - величина поверхности раздела твердое тело-жидкость; сн - концентрация насыщенного раствора; со - концентрация растворяющегося вещества в данный момент времени в объеме раствора; k - константа скорости.
Позже В. Нернстом была выдвинута теория, согласно которой скорость процесса на границе фаз (собственно растворение) значительно превосходит скорость диффузионного переноса вещества в объем раствора. Поэтому на границе фаз образуется насыщенный раствор и суммарная скорость процесса определяется молекулярной диффузией через слой раствора, прилегающий к поверхности твердого тела, в котором концентрация падает от сн до со. Концентрация в объеме раствора со поддерживается однородной благодаря хорошему перемешиванию. Сопоставление уравнения (XVIII.31) с уравнением Фика показывает, что k = D/Δ, где Δ - путь диффузии. Таким образом, уравнение (XVIII.31) может быть переписано в виде:
Q = (D/Δ)(cн - cо)S.
(XVIII.32)
Нернст полагал, что в слое, прилегающем к поверхности твердого тела толщиной Δ жидкость отличается измененными по сравнению со всей массой физико-химическими свойствами, и перенос вещества через этот слой осуществляется только путем молекулярной диффузии. Эти представления нашли качественное подтверждение в опытах А.Г. Самарцева, Путем оптических измерений он нашел, что в водных растворах вблизи поверхности твердого тела действительно существует тонкий слой жидкости, в котором имеется значительное изменение концентрации. Тем не менее теория Нернста лишь формально описывает процесс. Найденные из экспериментальных определений и вычисленные по уравнению (XVIII.32) величины Δ оказались имеющими порядок 10-2 - 10-3 см. Поскольку размер молекул имеет порядок 10-8 см, слой указанной толщины- соответствует 106 - 105 молекулярных слоев.
Очевидно, слой жидкости такой толщины не может, как это полагал В. Нернст, удерживаться в неподвижном состоянии
486
поверхности твердого тела силами молекулярного взаимодействия между твердым телом и жидкостью. Как отмечалось выше, Δ является лишь величиной эффективного пути диффузии.
Скорость перехода компонента из одной жидкости в другую, не смешивающуюся с ней (например, из стали в шлак), часто определяется величиной конвективного перемешивания в обеих фазах, возникающего в результате разницы температур, выделения пузырьков газа и пр. В таких случаях распределение скоростей течения и концентраций на границе двух жидкостей представляется более сложным, чем при движении жидкости относительно твердого тела. В связи с этим изложенные выше представления о пограничном слое могут быть использованы лишь для качественного рассмотрения кинетики реакций в системе, состоящей из двух жидкостей.
Рафинирование стали, т.е. извлечение вредных примесей (S, Р, О) из металла в шлаковый расплав, состоит из трех последовательных стадий: а) подвода реагирующих веществ из объема металла к его границе со шлаком; б) химической реакции на границе фаз; в) отвода продуктов реакции в объеме шлака.
При температурах сталеплавильного производства (1500-1600° C) константы скоростей химических реакций во многих случаях значительно превышают соответствующие величины, характеризующие массопередачу. Поэтому можно допустить, что суммарная скорость процессов рафинирования определяется величиной конвективной диффузии во взаимодействующих жидких фазах. Обычно металлический
и шлаковый расплавы интенсивно перемешиваются, особенно в период кипения, вызываемого выделением пузырьков СО, образующейся при окислении углерода, содержащегося в стали. Сопротивление переносу вещества описывается в этих случаях при помощи понятия эффективного пути диффузии.
Рассмотрим кинетику относительно простого процесса перехода серы из металла в шлак.
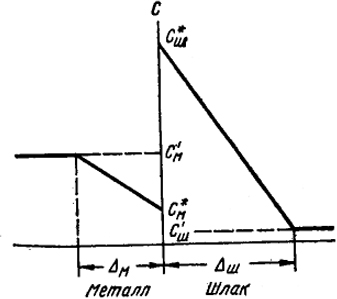
Рис. XVIII.4. Распределение концентрации серы в пограничных слоях металла и шлака
487
Распределение концентрации серы в пограничных слоях металла схематически представлено на рис. XVIII.4.
Примем, что процесс диффузии стационарен и концентрация серы на пути диффузии в пограничных слоях линейно изменяется в зависимости от расстояния от поверхности раздела. Найдем потоки серы в единицу времени Пм из объема металла к поверхности раздела и от этой поверхности в объем шлака Пш при величине поверхности раздела между фазами S:
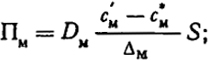(XVIII.33)
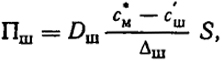(XVIII.34)
где Dм и Dш - эффективные коэффициенты диффузии серы в металле и шлаке; с
и
с
- концентрации серы в объеме металла и на границе со шлаком соответственно;
с
и
с
- концентрации серы в шлаке на границе с металлом и в объеме шлака соответственно; Δ
м и Δ
ш - пути диффузии серы в металле и шлаке.
Вводя коэффициенты массопередачи β
=
Dм/Δ
м и β
=
D/Δ
ш и выражая потоки серы в виде производных, показывающих количество перешедшего вещества в единицу времени, получим вместо уравнений (XVIII.33) и (XVIII.34)
dn/dτ = β(с
- с)S
(XVIII.35)
и
dn/dτ = β
(с
- с
)S.
(XVIII.36)
Для общности рассуждений допустим, что химическая стадия процесса - превращение серы на границе фаз (например, по реакции Sм → S-2 + 2e) - также может быть лимитирующей и что ее скорость описывается уравнением для реакций первого порядка. Ранее было показано, что скорость химической реакции первого порядка пропорциональна разности фактической и равновесной концентраций. Поэтому количество прореагировавшей серы пропорционально разности между ее фактической концентрацией в металле на границе со шлаком c
и ее концентрацией в металле, соответствующей равновесию со шлаком
с
= kx(c
- с
)S,
(XVIII.37)
488
где kx - константа скорости химической реакции.
Величина c
может быть найдена из справедливого для состояния равновесия соотношения
L =
c
/
с
, где
L - коэффициент распределения серы, откуда
c
=
c
/
L. Подставляя это соотношение в уравнение (XVIII.37), получим
= kx(c
- )S.
(XVIII.38)
Очевидно, если kx велика и химическая реакция не лимитирует развития процесса, то концентрация серы на границе фаз будет отвечать равновесию, т.е. c
=
с
/
L.
На границе фаз при стационарном течении процесса не происходит накопления серы. Поэтому должно соблюдаться равенство
(XVIII.39)
Скорость суммарного процесса должна быть пропорциональна разности между концентрацией серы в объеме стали и концентрацией, соответствующей равновесию со всей массой шлака см = с
/
L
= β’(c
- )S,
(XVIII.40)
где β’ - суммарный коэффициент массопередачи.
Разделим почленно уравнения (XVIII.35), (XVIII.36) и (XVIII.38) соответственно на произведения β
S, β
и
kxS. Кроме того, разделим обе части уравнения (XVIII.36) на
L:
·
=
c
-
c
;
=
-
;
·
=
c
-
.
Почленное суммирование этих уравнений дает
·
(
+
+
) =
c
-
.
489
Сопоставление этого уравнения с уравнением (XVIII.40) приводит к важному соотношению
+
+
=
.
Таким образом, обратная величина суммарного коэффициента массопередачи, в соответствии с уравнением (XVIII.8), равна сумме обратных величин β
,
kx и произведения β
. При условии, что
kx намного больше, чем β
и β
, суммарная скорость процесса определяется только массопередачей в металле и шлаке. В этом случае, приравнивая уравнения (XVIII.35) и (XVIII.36), найдем
β
= (
c
-
с)
S = β
(
c
-
с)
S.
Учитывая, что с
/
с
=
L, и исключая непосредственно неопределяемые величины
c
и
с
, получим после преобразований
= β
β
S.
(XVIII.41)
Поскольку шлак является более вязким, чем металл (β
< β
), то при небольших величинах
L можно пренебречь произведением
Lβ
по сравнению с β
этом случае из уравнения (XVIII.41) следует:
= β
S(Lc
- с)
(XVIII.42)
т.е. скорость процесса определяется массопередачей в шлаке. В случае, если величина L достаточно велика, то могут реализоваться условия, при которых можно пренебречь величиной β
по сравнению с
Lβ
в уравнении (XVIII.41), и тогда
= β
S(c
- ),
(XVIII.43)
т.е. скорость процесса лимитируется массопередачей в металле. При больших величинах L можно пренебречь величиной c
/
L (особенно в начальный период), и тогда из уравнения (XVIII.43) следует:
= β
Sc
.
490
В этом случае кинетика десульфурации, как это было показано опытным путем, подчиняется уравнению для реакций первого порядка. Из сказанного видно, что кинетика процесса в рассмотренном случае зависит не только от коэффициента массопередачи, но и от термодинамического фактора, определяемого величиной L. Приведенные кинетические уравнения для процесса десульфурации показывают, что увеличение интенсивности перемешивания должно привести к ускорению процесса (при условии, что kx достаточно велика). Количественные характеристики, дающие связь между скоростью десульфурации и условиями перемешивания, могут быть получены с использованием безразмерных комплексов.
Следует отметить, что из уравнения (XVIII.40) для суммарного процесса легко найти изменение концентрации серы в металле в зависимости от времени. Если массу металлической ванны обозначить Gм, то при dn/Gм = dc
найдем скорость уменьшения концентрации серы в металле:
-
= β’
(
с
-
).
Отсюда видно, что скорость реакции при прочих равных условиях прямо пропорциональна поверхности раздела фаз и обратно пропорциональна массе металла (или глубине металлической ванны).
Задача, подобная рассмотренной выше, возникает при анализе процессов растворения газов в жидкостях. Опытные данные о растворении газов в жидкостях указывают на то, что непосредственно на границе фаз устанавливается равновесие вследствие более быстрого протекания химического взаимодействия по сравнению с процессами массопередачи.
Количество вещества, перенесенного из одной фазы в другую в единицу времени через единицу поверхности раздела при стационарном течении процесса, определяется соотношением
()() = β
(p’ - p*) = β
(с* - с’),
(XVIII.44)
где β
и β
- коэффициенты массопередачи в газе и жидкости;
р’ и
р* - парциальные давления растворяющегося вещества в объеме газовой фазы и на границе с жидкостью;
c* и
с’ - соответственно концентрации этого вещества в жидкости на ее поверхности и в объеме.
491
Схематически распределение давления и концентрации в зависимости от расстояния от границы раздела фаз показаны на рис. XVIII.5 и XVIII.6 для хорошо и плохо растворимых газов.
В случае хорошо растворимых газов в жидкой фазе концентрация резко падает при удалении от поверхности раздела.
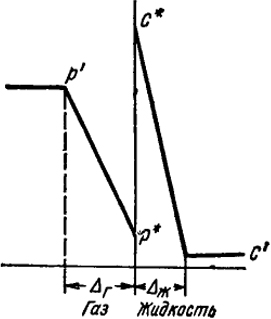
Рис. XVIII.5. Распределение давления и концентрации в случае хорошо растворимого газа
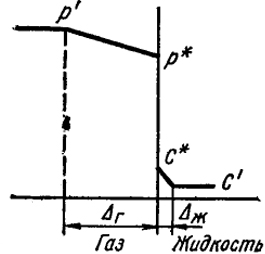
Рис. XVIII.6. Распределение давления и концентрации в случае плохо растворимого газа
Поэтому растворяющееся вещество (газ) будет быстро отводиться в объем жидкости так, что величина р* поддерживается очень малой. Такой случай реализуется, например, при растворении HCl или NH3 в воде. В подобных случаях в уравнении
(
)(
) = β
(
p’ -
p*)
можно пренебречь величиной р* по сравнению р’ и оно будет иметь вид:
(
)(
) = β
p’.
В жидких металлах растворимость газов мала. В этом случае концентрация в жидкости немного уменьшается с расстоянием и отвод газа от поверхности раздела совершается медленно. Соответственно мало падение давления
492
растворяющегося вещества в газовой фазе. Вследствие этого концентрация на поверхности жидкости отвечает равновесию с газовой фазой (c
) при давлении
р*, которое немного отличается от
р’. Таким образом, массопередача в газовой фазе происходит достаточно быстро и не лимитирует скорость процесса. В этом случае кинетическое уравнение (XVIII.44) принимает вид:
()() = β(с
- с’).
(XVIII.45)
Для растворов двухатомных газов в металлах, как указывалось в гл. V, между парциальным давлением и концентрацией существует соотношение c = k√p.
Принимая это во внимание, перепишем уравнение (XVIII.45):
()() = β
k(√pравн - √p’) = α(√pравн - √p’),
(XVIII.46)
где pравн - парциальное давление, соответствующее равновесной концентрации на поверхности жидкости; р’ - парциальное давление, соответствующее равновесию с фактической концентрацией в объеме жидкости.
Разделив обе части уравнения (XVIII.45) на массу жидкости (металла) Gм, получим:
=
(
с
-
с’).
Таким образом, при постоянных температуре и давлении для данной массы металла изменение концентрации газа в жидкости во времени передается уравнением
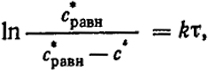
где k = β
S/
Gм.
Подобная зависимость наблюдается, например, при растворении азота в жидком железе.
493
