При реакциях между флюидными фазами (газами и жидкостями) и твердыми телами или газами и жидкостями при достаточно малых скоростях потока в движущейся фазе лимитирующим звеном оказывается внешняя массопередача (диффузия). При увеличении скоростей внешних потоков лимитирующей становится внутренняя диффузия. Естественно, что скорости внутридиффузионных процессов не зависят от скорости внешнего потока.
Рассмотрим особенности процессов внешней массопередачи. В подобном процессе поток газов (или смеси газов) омывает зернистый материал. Газ реагирует с этим материалом или поглощается. Пусть скорость газового потока будет α. Концентрация реагирующего вещества в газе с и концентрация на границе зерен сх. Скорость процесса, измеряемая количеством прореагировавшего (или поглощенного) вещества в единице объема слоя a в единицу времени da/dτ, определяется уравнением:
da/dτ = β(c - cx),
(XVIII.16)
где β - коэффициент массопередачи.
В случае, если скорость диффузии в глубину зерна настолько велика, что сх очень мала, то уравнение (XVIII.16) можно записать в виде:
da/dτ = βc.
(XVIII.17)
Признаками того, что процесс определяется условиями внешней массопередачи, являются: ;
- 1) величина β зависит от скорости потока, т.е. β = f(α), и от природы газоносителя и не зависит от пористости твердого тела;
- 2) диффузионное сопротивление не зависит от времени;
- 3) если процесс прерывается и после некоторого перерыва вновь продолжается в тех же условиях, то его кинетика будет характеризоваться теми же параметрами, что и до перерыва. Иными словами, у процесса отсутствует явление "памяти";
474
- 4) скорость процесса сравнительно мало зависит от температуры.
При увеличении скорости потока газа (или жидкости) скорость внешней массопередачи окажется больше, чем внутренней, и при определенных условиях протекание процесса станет определяться не внешней', а внутренней массо-передачей.
В реальных условиях внешняя массопередача является сложным, процессом, определяющимся, с одной стороны, молекулярной диффузией, а с другой - непосредственной передачей вещества благодаря наличию скорости потока. Такой процесс суммарного подвода вещества называется конвективной диффузией. Для количественного расчета этого процесса необходимо знать закон, по которому меняется скорость истока в зависимости от расстояния от обтекаемого тела. Решение задачи о диффузии из потока требует учета как законов, описывающих течение жидкости (для случая вязкой жидкости - уравнений Навье-Стокса), так и законов диффузии.
В часто встречающихся на практике задачах, например в случаях обтекания зернистого материала, невозможен абсолютный расчет. Это обусловлено невозможностью учета всех геометрических особенностей обтекания зернистого материала потоком. В таких случаях целесообразно пользоваться методами теории размерностей, которая позволяет свести к минимуму число необходимых измерений для описания всего процесса, а также дает возможность установить законы подобия, позволяющие осуществлять моделирование процессов.
В основе этой теории лежит требование совпадения размерности обеих частей равенств, выражающих связь между физическими величинами. Целесообразнее всего удовлетворить это требование, если выражать физические зоны в виде соотношений между безразмерными комплексами. Теория размерностей, таким образом, позволяет излагать законы природы в форме, не зависящей от выбранных единиц. Это обстоятельство, в частности, используется для контроля физических расчетов, поскольку в применяемых уравнениях должны совпадать размерности их правых и левых частей. Теория размерностей дает возможность предсказания некоторых физических соотношений, если заранее известно, какие величины могут влиять на изучаемое явление. Рассмотрим простой пример, относящийся к зависимости давления идеального газа Р от объема V. Молекулы такого газа можно считать математическими точками и давление должно зависеть от. следующих величин: массы одной молекулы m, средней скорости молекул u, от их числа п в единице объема n/V. Следовательно, P = f(m, и, n/V). Обозначим размерность длины через L, массы через T и времени через Т. Интересующие нас величины имеют размерности: P - L-1MT-2, m - М, и - LT-1 и n/V - L-3. Предполагая, что функция f степенная, введем пока неизвестные показатели степени х, у, z для размерностей m, u и n/V соответственно.
475
Тогда уравнение
P =
f(
m,
и,
n/V) можно записать в виде
L-1MT-
= Mx(LT-1)y(L-3)z.
Условием совпадения размерностей здесь является равенство показателей степенен при М, L и Т в обеих частях уравнения. Легко видеть, что х = 1, у - 3z = -1, y = 2, откуда z = 1. Таким образом, Р = Cmu2n/V, где С - безразмерный коэффициент пропорциональности, Так как при постоянной температуре и постоянна, то PV = const, т.е. мы получили закон Бойля.
Таким образом, при решении конкретных задач при помощи теории размерностей первым является определение числа независимых безразмерных комплексов и их выбор. Согласно так называемой π-теореме, число независимых безразмерных комплексов равняется числу рассматриваемых величин, за вычетом числа использованных элементарных размерностей (длина, время, масса). Смысл этой теоремы будет ясен из дальнейшего изложения.
В рассматриваемой задаче обтекания твердого тела текучим (газом или жидкостью) скорость процесса выражается при помощи коэффициента массопередачи β. От каких факторов может зависеть β? Естественно принять, что коэффициент массопередачи зависит от скорости потока α, размера обтекаемого тела d, коэффициента диффузии вещества D и свойств флюидной фазы, характеризующихся вязкостью η и плотностью ρ.
Таким образом, согласно π-теореме, число безразмерных комплексов должно быть равно 3(6 - 3 = 3). Чтобы доказать это, напишем выражение для безразмерного комплекса K:
βxαydzDmηnρt = K,
(XVIII.18)
где х, у, z, т, п и t - некоторые неизвестные пока положительные или отрицательные показатели степеней; K - безразмерный комплекс. Это уравнение содержит шесть неизвестных.
Подставив в уравнение (XVIII. 18) размерности β, α, d, D, и ρ, получим
(1/T)x(L/T)y(L)z(L2/T)m(M/LT)n(M/L3)t = K.
(XVIII.19)
Условия безразмерности величины K сводятся к тому, чтобы сумма показателей степеней при элементарных размерностях в левой части уравнения (XVIII.19) была равна нулю. Отсюда для показателей при Т, L и М получаем
Т ... - х - у - m - n = 0;
L ... - у + z + 2т - n -3t = 0;
M ... n + t = 0.
(XVIII.20)
476
Если бы число неизвестных было равно трем, то выписанных уравнений было бы достаточно для их определения. Так как число неизвестных равняется 6, то 3 из них мы можем выбрать произвольно. Покажем, что эти три произвольно выбранных параметра приведут к трем безразмерным комплексам в соответствии с π-теоремой. Выберем в качестве трех переменных п, т и у. Тогда все остальные неизвестные (х, z и t) могут быть определены из уравнений (XVIII.20) через п, т и у:
x = m - n - y;
z = 2m - 2n - y;
t = -n.
Подставим найденные значения х, z и t в уравнение (XVIII.19) и соберем члены, содержащие п, m и у. Тогда уравнение (XVIII.19) примет вид
β-m-n-yαyd-2m-2n-yDmηnρ-n = K
или
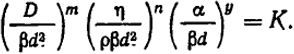
Так как т, n и y - произвольные величины, то K может быть безразмерной величиной только в том случае, если каждое из выражений в скобках безразмерно. Таким образом, мы получаем три безразмерных комплекса:
K1 =
,
K2 =
,
K3 =
.
Очевидно, что полученный результат соответствует требованию π-теоремы и сделанный расчет по существу является ее выводом. Действительно, в общем случае если имеется Р физических переменных, то число неизвестных также равно Р, а число уравнений будет определяться числом использованных размерностей q. Поэтому произвольно можно выбрать (Р - q) неизвестных, а число этих неизвестных, равно числу безразмерных комплексов. Комплексы K1, K2, K3 являются независимыми, однако, используя их, можно получить другие безразмерные комплексы, зависящие от этих трех.
Комбинированием K1, K2 и К3 мы получим следующие наиболее часто используемые комплексы. В качестве первого из них примем просто K1-1, который называется критерием, или числом Нуссельта и обозначается Nu = βd2/D.
477
В качестве второго примем отношение K3/K2, которой называется критерием Рейнольдса: Re = αdρ/η. Наконец, третий критерий, представляющий собой отношение K2/K1, называется критерием Прандтля: Pr = η/ρD. Рассмотрим кратко смысл.этих критериев.
Критерий Нуссельта выражен через величину β, определяющую поток в единице объема зерненного материала. В случае обтекания одного тела (шар, цилиндр, пластина) или течения в трубе целесообразно поток относить к единице поверхности этого тела и использовать коэффициент массопередачи β′ и соответственно критерий Nu′ = β′d/D.
Критерий Нуссельта характеризует массопередачу. Следует различать внешнюю и внутреннюю задачи массопередачи. При обтекании тела имеют дело с внешней задачей, при движении потока внутри тела, например трубы, - с внутренней задачей. При диффузии к какому-либо телу в отсутствие потока критерий Nu(Nu′) имеет постоянное значение, что является выражением закона Фика. Действительно, поток к поверхности величиной S при стационарном режиме П = DcSNu′cS.
Выразив β′ через критерий Nu′, получим :
П = DcSNu′/d.
В этом уравнении d характеризует путь диффузии, а критерий Nu′ должен быть постоянным, зависящим от формы тела. Для диффузии к шару в отсутствие потока Nu′ = 2. Это отвечает известной формуле Лангмюра для потока к шару радиуса r (или от шара). В этом случае S = 4πr2, так что, приняв Nu′ = 2, получим
П = 4πrDc.
(XVIII.21)
Выведем формулу Лангмюра для случая диффузии к шару. Уравнение диффузии
D [
+
+
] =
.
целесообразно переписать в сферических координатах, т.-е.
(
r2
) =
.
При стационарном режиме ∂с/∂τ = 0 и r2(∂c/∂r) = A, где А - постоянная.
Отсюда ∂с/∂r = А/r2, что после интегрирования дает c = -A/r + B, где В - постоянная.
Величины А и В определяются из краевых условий.
478
При диффузии к шару c∞ = с0 и сr0 = 0, где r0 - радиус шара.
Таким образом,
c = c0(1 - ).
(XVIII.22)
Поток
П = D4πr
(
)
r=r0.
Из уравнения (XVIII.22) следует, что (∂c/∂r)r=r0 = c0/r0, отсюда получается формула Лангмюра (XVIII.21).
Таким образом, мы показали, что в отсутствие течения для шара Nu′ = 2.
Величина критерия Нуссельта имеет постоянное значение не только для внешней задачи при отсутствии течения, но и для внутренней задачи при ламинарном потоке. Если жидкость протекает по длинной трубе, то а отсутствие завихрений скорость направлена перпендикулярно к пути диффузии (радиусу трубы) и не приводит к подводу вещества к стенкам. Опыт показывает, что для длинных труб Nu′ = 3,66. В коротких трубах на передаче вещества сказывается особенность потока у начала трубы.
Критерий Рейнольдса определяет характер потока вещества. Можно показать, что безразмерный комплекс, включающий сопротивление потоку (определяемое падением давления) - так называемый приведенный коэффициент трения, зависит от числа Рейнольдса. При этом в случае малых скоростей эти два безразмерных комплекса пропорциональны друг другу. Здесь сопротивление не зависит от плотности текучего, а только от вязкости и пропорционально скорости потока.
При некотором критическом значении числа Рейнольдса наступает более или менее резкий переход к другому закону, связывающему два упомянутых выше безразмерных комплекса. В этом новом режиме сопротивление не зависит от вязкости, а определяется плотностью текучего и пропорционально скорости в степени, приближающейся к 2. Это критическое значение числа Рейнольдса для труб лежит в пределе 2100 - 2300 (при этом Rе = αdρ/η, где d - внутренний диаметр трубы).
Для случая внешнего обтекания критическое значение лежит между 20 и 30, a d представляет собой диаметр обтекаемых частиц. Рассматриваемый переход при критических
479
значениях Re означает изменение режима от ламинарного к турбулентному. Для ламинарного потока характерно установившееся слоистое течение. При ламинарном движении жидкости в трубе скорости во всем сечении практически параллельны оси трубы. Для турбулентного движения характерно наличие хаотических вихрей.
При значениях Re меньших критического, устойчив ламинарный режим. Если какое-либо возмущение (например, неровности в стенках трубы или на поверхности обтекаемого тела) вызовет разрушение ламинарности, то на некотором расстоянии поток вновь станет ламинарным. При числах Рейнольдса выше критических такого восстановления ламинарного режима не будет.
Третий критерий - Прандтля - характеризует определенные физико-химические свойства самого текучего (газа или жидкости).
В гл. XIV было показано, что для D = 1/3 λu и ν = 1/3 λuρ. Отсюда следует, что для идеальных газов Pr = 1. Для жидкостей обычно η = 10-2г/(см·с), ρ = 1г/см3, D = 10-5см2/с. Отсюда критерий Прандтля для обычных жидкостей равен приблизительно 103.
Из сказанного следует, что критерий Нуссельта должен, зависеть как от характера течения (Re), так и от свойств текучего (Pr). Поэтому зависимость коэффициента массопередачи от параметров опыта следует искать в виде соотношения Nu = f(Re, Pr). Так как для газов Pr = 1, то в этом случае величина Nu зависит только от Re.
Таким образом, рационально из опытных значений зависимости р от одного из параметров опыта найти связь между Nu и Re. Целесообразно при графическом изображении этой зависимости откладывать логарифмы числа Нуссельта против логарифма числа Рейнольдса. Это имеет смысл потому, что для заданного режима течения можно ожидать Nu = k(Re)n. Тогда на билогарифмическом графике должна иметь место прямолинейная зависимость. Опыт действительно дает в определенных условиях такую зависимость (рис. XVIII.3).
Резкое изменение характера кривой отвечает критическому значению числа Re и соответствует переходу течения из ламинарного в турбулентное. Для получения зависимости Nu-Re достаточно определить изменение р с изменением лишь одного параметра, например скорости. Зависимости от остальных параметров (размеров тела, природы газа) могут быть рассчитаны. В этом проявляется основное
480
преимущество метода размерностей, которое позволяет свести к минимуму число необходимых измерений.
Кроме того, теория размерностей лежит в основе учения о подобии. Действительно, мы видим, что характер режима течения будет одинаков, несмотря на различия в размерах обтекаемых тел, если под- и Re держивается постоянное значение критерия Рейнольдса. Например, если мы хотим при уменьшении диаметра трубы в 100 раз сохранить подобие, то необходимо увеличить скорость тоже в 100 раз или использовать текучее, имеющее кинематическую вязкость η/ρ, в 100 раз меньшую.
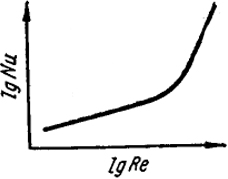
Рис. XVIII.3. Связь между величинами критериев Nu и Re
Мы не будем останавливаться здесь на сложной теории моделирования и подобия. Из сказанного выше ясно, что для развития этой теории много дает теория размерностей. Для ламинарного режима и внешней задачи, как показывает опыт, величина Nu′ пропорциональна корню квадратному из числа Re. В частности, для обтекания шара Nu′ = 0,54√Re (при ламинарном режиме и не слишком малых числах Re, т .е. больших 200).
Соотношение Nu′ = k√Re можно описать на основе понятия пути диффузии. Из закона Фика следует, что
П = DSc0/Δ,
(XVII1.23)
где Δ - путь диффузии, т.е. эффективное расстояние, на котором совершается перепад концентраций от с0 до 0. При расчете предполагается, что на расстоянии Δ концентрация падает линейно.
Таким образом, реальное сложное распределение концентрации заменяется некоторым условным, в котором концентрация меняется линейно, и при этом обеспечивается тот же поток, что и при реальном распределении.
Сравнивая формулу Лангмюра (XVIII.21) с уравнением (XVIII.23), находим, что Δ = r0. Это не значит, однако, что на расстоянии r0 от поверхности шара концентрация равняется с0 и весь перепад концентрации от с0 до 0 происходит на этом расстоянии. Из уравнения c = c0(1 - r0/r) видно, что в точке r = 2r0 c = c0/2. Таким образом, понятие пути диффузии носит условный характер. Из уравнения (XVIII.23) следует, что β′ = D/Δ и Nu′ = d/Δ, а из соотношения
481
Nu′ ≈ √Re вытекает, что
Δ = d/√Re.
(XVIII.24)
Мы видим, таким образом, что при увеличении скорости потока путь диффузии уменьшается. Как следует из уравнения (XVIII.24), путь диффузии обратно пропорционален квадратному корню из числа Рейнольдса.
С понятием о пути диффузии и соотношениями, описывающими его зависимость от скорости потока, связан ряд упрощенных концепций, сыгравших, однако, положительную роль на первых этапах развития кинетики гетерогенных процессов (А.Н. Шукарев, В. Нернст, Нойес, И. Лангмюр). Согласно этим концепциям, на поверхности твердого тела образуется слой текучего с измененными физико-химическими свойствами. Так, например, по наиболее примитивным представлениям принималось, что этот слой неподвижен и является непромешиваемым. Допускалось, что с увеличением скорости потока меняется лишь толщина этого слоя.
Согласно представлениям гидродинамики, при обтекании твердого тела скорость текучего на его поверхности должна равняться нулю. В некотором слое, называемом пограничным, тангенциальная составляющая скорости потока увеличивается от значения, равного нулю, до некоторого значения, характерного для объема потока. Решение соответствующих уравнений гидродинамики в случае ламинарного режима показывает, что величина пограничного слоя обратно пропорциональна квадратному корню из числа Рейнольдса. Так как диффузионное сопротивление лежит в основном в пограничном слое, то понятно, почему путь диффузии также обратно пропорционален √Re. Мы выведем важное соотношение (XVIII.24) на основе следующего наглядного, но качественного рассуждения. Между путем диффузии Δ и временем диффузии существует соотношение (см. гл. XIV) D ≈ Δ2/τ.
Время, в течение которого частица из потока имеет возможность диффундировать к поверхности тела, имеющего размер d, определяется соотношением τ = d/α, где α - скорость потока. Отсюда Δ ≈ √Dτ или Δ ≈ √Dd/α. Выше отмечено, что для газов число Прандтля Pr = η/ρD = 1, т.е. D = η/ρ. Тогда Δ ≈ d√ρ/αdη ≈ d/Re.
Молекулярная диффузия в отсутствие потока описывается уравнением диффузии, выведенным в гл. XIV.
Для вывода уравнения конвективной диффузии при
482
проведении баланса вещества следует учесть наличие потоков. Для простоты рассмотрим одномерную задачу. Так же, как и при выводе уравнения диффузии, определим увеличение количества вещества в элементарном объеме SΔx за время Δτ, обязанное наличию потока. Через левую плоскость, отсекающую этот объем, за время Δτ количество вошедшего вещества составит αSc(x)Δτ, а количество вышедшего - αSc (x + Δх)Δτ. Таким образом, увеличение количества вещества из-за потока составит
aS[c(x) - c(x + Δx)]Δτ = -αS
Δ
xΔτ.
Если далее провести материальный баланс с учетом молекулярной диффузии, то получим уравнение конвективной диффузии
-α
+ D
=
.
(XVIII.25)
Аналогичный вывод для трехмерной задачи дает
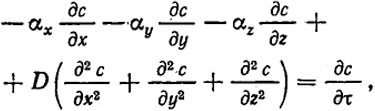 (XVIII.26)
(XVIII.26)
где αх, αу и αz - составляющие скорости.
Это уравнение является основой для расчетов, связанных с работой химической аппаратуры.
Описание скоростей реакций в каких-либо слоях в условиях переменной концентрации внутри слоя и при наличии потока является задачей, относящейся к области динамики процессов (например, динамика сорбции, восстановление оксидов, катализ).
Важно отметить, что количество вещества может изменяться не только вследствие диффузии и скорости, но и в результате того, что текучее может поглощаться или реагировать. Поэтому к правой части равенства (XVIII.25) должен быть добавлен член
, где α - количество поглощенного или прореагировавшего вещества в данном месте слоя. Соответственно уравнение (XVIII.25) можно переписать в виде
-α
+ D
=
+
.
(XVIII.27)
В качестве примера применения этого уравнения рассмотрим
483
следующий простой случай. Пусть через слой железной руды со скоростью α протекает инертный газ, содержащий газ-восстановитель с концентрацией c. Допустим, что скорость потока настолько велика, что вторым членом в левой части уравнения (XVIII.27) можно пренебречь. В соответствии с изложенным выше, da/dτ = βc; при этом мы полагаем, что скорость процесса определяется внешней, а не внутренней диффузией, что всегда бывает на начальных стадиях процесса.
Так как скорость подвода восстановителя при внешнем диффузионном режиме не зависит от времени, то наступает стационарное состояние, при котором ∂c/∂τ = 0. Следовательно:
-α
=
= β
c.
Это уравнение при учете краевого условия с(x = 0) = c0 имеет следующее решение:
c = c0e-βx/α.
(XVIII.28)
Отсюда следует, что на расстоянии α/β = x концентрация газа-восстановителя падает в е раз.
В уравнении конвективной диффузии учитывается подвод вещества как благодаря молекулярной диффузии, так и вследствие потока. Для сравнения доли участия этих двух источников целесообразно привести уравнение (XVIII.26) к безразмерному виду. Пусть характерный размер обтекаемого тела равен d, а скорость текучего α. Введем безразмерные величины x’ = x/d; y’ = y/d; z’ = z/d; α
= α
x = α
x/α; α
y = α
y/α; α
z = α
z/α;
c’ =
c/
c0 (
с0 - концентрация вещества в потоке вдали от тела). После подстановки и простых преобразований получим для стационарной задачи ∂
c/∂τ= 0 следующее решение:
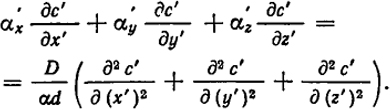 (XVIII.29)
(XVIII.29)
Так как все величины в этом уравнении безразмерны, то и множитель в его правой части D/αd также должен быть безразмерным. Обратная величина этого множителя называется критерием Пекле: Pe = κd/D. Этот критерий непосредственно характеризует отношение потоков, обязанных скорости и диффузии. При малых значениях числа Ре можно пренебречь левой частью равенства (XVIII.29)
484
и процесс описывается только уравнением молекулярной диффузии. Мы показали раньше, что независимых критериев в рамках рассматриваемой задачи может быть только три. Действительно," легко убедиться, что Pe = Re·Pr.
Так как для жидкостей число Прандтля на три порядка больше, чем для газов, то при одинаковых числах Рейнольдса число Пекле для жидкостей в 1000 раз больше, чем для газов. Это означает, что благодаря малости коэффициента диффузии в жидкостях основная часть переноса вещества обязана конвекции. В газах скорость молекулярного переноса настолько велика, что конвективный перс-нос играет значительно меньшую роль, чем в жидкостях.
Рядом ученых, в частности в СССР, решены задачи конвективной диффузии для важных практических случаев (диффузия к поверхности вращающегося диска, к падающей частице, к обтекаемой пластинке и пр.).
Для эффективного пути диффузии было найдено, что
Δ = D1/3ν1/6√x/α,
(XVIII.30)
где х - расстояние от точки набегания потока на тело ν = η/ρ.
Рассмотрение массопередачи для турбулентных потоков может основываться на двух принятых в настоящее время представлениях. Согласно концепции Кармана, вблизи поверхности твердого тела имеется ламинарный слой, затем в некотором "буферном" слое турбулентность нарастает до значения, характерного для объема потока, и, наконец, имеется область турбулентного потока. Естественно, что основное сопротивление переносу, особенно для жидкостей, лежит в ламинарном слое.
Согласно теории, развитой Л.Д. Ландау, турбулентность постепенно уменьшается при приближении к твердому телу, но сохраняется вплоть до его поверхности. Уравнения для массопередачи, получаемые на основе обеих теорий, близки между собой.
485
