Гетерогенными называются реакции, происходящие между веществами, находящимися в различных соприкасающихся фазах. Такие реакции распространены в природе и технике.
Все химические реакции; происходящие при производстве металлов и сплавов, а также при их термической и механической обработке, являются гетерогенными. Можно привести много примеров гетерогенных реакций, имеющих значение в металлургическом производстве:
- 1) горение твердого и жидкого топлива;
467
- 2) восстановление твердых оксидов газами или углеродом;
- 3) распределение веществ между жидкими фазами (металл-шлак, металл-штейн);
- 4) процессы растворения и выделения газов из металла и шлака;
- 5) процессы растворения твердых тел в жидкостях (например, футеровки сталеплавильных печей в шлаках);
- 6) кристаллизация жидкостей (например, затвердевание стальных слитков);
- 7) фазовые превращения в твердых металлах и сплавах.
Отличительными особенностями всех гетерогенных процессов являются их сложность и многостадийность. Обычно гетерогенная реакция состоит, по меньшей мере, из трех стадий.
Первая стадия заключается в переносе реагирующих веществ к поверхности раздела фаз - реакционной зоне.
Второй стадией является сама гетерогенная химическая реакция (например, окисление фосфора, растворенного в жидкой стали, продуваемым через нее кислородом, или восстановление оксидов металлов водородом).
Третья стадия заключается в отводе продуктов реакции из реакционной зоны. Так как скорости процессов во всех стадиях пропорциональны величине поверхности, то скорости гетерогенных реакций должны зависеть от отношения между величинами поверхности раздела фаз и объема. Стадией, определяющей скорость (контролирующей процесс), является наиболее медленная. Процессы переноса реагирующих веществ, осуществляющиеся на первой и третьей стадиях, называются массопередачей.
В процессах массопередачи различают внешнюю и внутреннюю массопередачу. В качестве примера процесса, в котором в зависимости от условий скорость может определяться либо внешней, либо внутренней массопередачей, рассмотрим восстановление закиси железа. При обычных для верхних горизонтов доменной печи температурах собственно химическое превращение
FeOт + СОг = Feт + CO2г
происходит со скоростью, значительно большей, чем массо-передача, и поэтому эта стадия не лимитирует протекание всего процесса. Массопередача осуществляется как благодаря диффузии в газовом потоке, так и в массе частично восстановленной руды. Первый процесс называется внешней массопередачей, а второй - внутренней.
468
Внутренняя диффузия представляет собой ряд параллельных процессов. Одним из них является обычная диффузия газов по капиллярам сравнительно большого радиуса; другим - капиллярная диффузия по узким капиллярам. Если длина свободного пробега больше диаметра капилляра, то диффузионное блуждание молекул определяется не столкновениями между собой, а столкновениями со стенками (см. гл. XIV). Третьим процессом является поверхностная диффузия, осуществляющаяся адсорбированными молекулами по стенкам капилляров. Помимо этого, возможна диффузия в твердом состоянии через образовавшийся слой продукта реакции (железа).
Суммарная скорость гетерогенного процесса определяется скоростями отдельных его звеньев или стадий. Как указывалось выше, если скорость одной из последовательных стадий процесса значительно меньше других, то суммарная скорость определяется скоростью этой наиболее медленной стадии. Если же скорости отдельных стадий сравнимы между собой, то суммарная скорость реакции не обязательно должна быть равна скорости самой медленной стадии, так как все стадии взаимно связаны. Протекание более быстрых стадий может оказывать влияние на скорость медленной стадии.
Если наиболее медленным звеном процесса является подвод реагирующих веществ к зоне реакции или отвод из нее продуктов реакции, то кинетика суммарного процесса будет диффузионной. О таких процессах также говорят как об идущих в диффузионной области. В случае, если медленная стадия процесса заключается в химическом или физическом превращении, то скорость процесса определяется скоростью реакции, и процесс лежит в кинетической области.
При сравнимых скоростях диффузии и химического превращения имеет место промежуточная область реакций. Сказанное справедливо для сложных процессов, состоящих из нескольких последовательных стадий. В случае, если гетерогенный процесс состоит из ряда одновременно протекающих параллельных процессов, как например при внутренней диффузии, то определяющим является самый быстрый процесс.
В качестве примера последовательного процесса рассмотрим случай стационарной диффузии при переносе вещества через две фазы I и II, имеющие различную проницаемость и толщины, равные hI и hII соответственно. Этот процесс схематически представлен на рис. XVIII.1. Будем
469
поддерживать на внешней поверхности фазы I постоянную концентрацию с0, а на внешней поверхности фазы II - концентрацию диффундирующего вещества, равную нулю. При этом на границе между фазами возникает не зависящая от времени концентрация сх. Отметим, что при стационарном процессе распределение концентрации диффундирующего вещества в среде, в которой происходит диффузия, не зависит от времени, т.е. в каждой точке этой среды концентрация сохраняет постоянную величину. Кроме того, концентрация с при этом обязательно должна линейно зависеть от расстояния х. Действительно, из уравнения диффузии
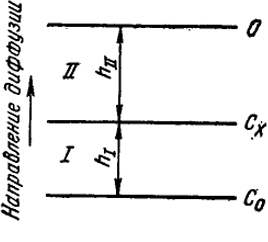
Рис. XVIII.1. Схема стационарной диффузии

Рис. XVIII.2. Схема параллельного процесса
D(∂2c/∂x2) = ∂c/∂t следует, что при ∂c/∂t = 0 и ∂2с/∂х2 = 0, т.е. ∂с/∂х является постоянной величиной. Таким образом, зависимость концентрации от расстояния выражается уравнением.
c = ax + b,
(XVIII.1)
где а и b - постоянные.
Такое распределение концентрации осуществляется, например, при диффузии газов через диафрагмы.
Каким способом в подобных случаях влияют на скорость процесса, состоящего из последовательных звеньев, величины диффузионных сопротивлений? Поток вещества (П1) через фазу I определяется уравнением:
П1 = D1
= β
(c0 - cx),
(XVIII.2)
где DI - коэффициент диффузии в фазе I, а отношение β
=
DI/
hI (или β′ =
D/
h) называется
коэффициентом массопередачи и имеет размерность ем/с.
470
Часто коэффициент массопередачи рассчитывают из величины потока не на 1 см2, а на 1 см3 объема, заполненного зерненным материалом р. Так как поверхность материала в единице объема обратно пропорциональна диаметру частицы d, то β = β′/d и, следовательно, имеет размерность см/с. Вообще говоря, величины β′ характеризуют массопередачу не только в случае молекулярной диффузии, но и при любом другом виде переноса вещества. Поток вещества в фазе II составляет:
ПII = (DII/hII)(cx - 0) = β
cx.
(XVIII.3)
Величина общего потока определяется соотношением:
П = β’c0
(XVIII.4)
В условиях стационарности
ПI = ПII = П,
(XVIII.5)
так как вещество не может накапливаться в любом месте среды.
Какова связь между величинами β
, β
и β′?
Из уравнения (XVIII.5) следует, что β
(
c0 -
cx) = β
cx. Отсюда концентрация на границе фаз
cx = β
c
/ (β
+ β
).
(XVIII.6)
Учитывая это, величину общего потока Я можно выразить уравнением:
П = ПII = β
cx = [β
β
/ (β
+ β
)]c0.
(XVIII.7)
Сопоставляя уравнения (XVIII.7) и (XVIII.4), видим, что
β’ = β
β
/ (β
+ β
)
или
1/β’ = 1/β
+ 1/β
.
(XVIII.8)
Величины 1/β′ носят общее название сопротивлений. Таким образом, из уравнения (XVIII.8) следует, что в последовательных процессах общее сопротивление 1/β′ равно сумме частных сопротивлений.
Рассмотрим некоторые случаи, которые могут осуществляться при последовательных процессах. Пусть, например, сопротивление фазы II значительно больше, чем фазы I (очевидно, соотношение между проводимостями будет обратным, т.е. β
≪ β
). Это позволяет пренебречь слагаемым
471
1
уравнении (XVIII.8), следовательно, в этом случае β′ = β
.
Если проводимость фазы I β
значительно больше, чем β
, то, пренебрегая последней величиной в уравнении (XVIII.6), видим, что
сх =
с0, т.е. что отсутствует градиент концентрации в фазе I. Это показывает, что скорость процесса, состоящего из последовательных стадий, очень сильно отличающихся своими сопротивлениями, зависит от стадии с наибольшим сопротивлением.
В металлургической практике встречаются случаи, когда процесс заключается в диффузии вещества к поверхности, на которой оно вступает в химическую реакцию. Поток диффузии пропорционален, как это было показано, градиенту концентраций.
Покажем, что скорость химической реакции первого порядка пропорциональна разнице фактической и равновесной концентраций.
Пусть в системе, где происходит реакция A ←→ B, вещества А и В имеют концентрации СА и сB. Тогда ω = k1cA - k2cB.
Концентрация А, которая отвечала бы равновесию с В (при ω = 0), определяется уравнением: k1c
=
k2cB. Таким образом ω =
k1(
cA -
c).
Если система далека от равновесия, то ω = k1cA.
В качестве примера наложения диффузионного и химического процесса рассмотрим обезуглероживание поверхностного слоя стали при ее нагреве в восстановительной атмосфере, например, в водороде. Здесь углерод диффундирует к поверхности металла, на которой происходит реакция
C + 2H2г = CH4г.
Для малых времен можно считать концентрацию углерода внутри металла постоянной (с0). Будем считать процесс стационарным. Пусть на поверхности стали устанавливается концентрация углерода, равная с, которая остается постоянной в течение всего процесса, поскольку ее убыль в результате химической реакции компенсируется вследствие диффузии углерода из объема металла. Диффузионный поток к поверхности металла
П + β′(c0 - cп).
(XVIII.9)
Примем для простоты, что химическая реакция имеет первый порядок с константой скорости k и что система далека от равновесия. Тогда
ω = kcп.
(XVIII.10)
472
Из условия стационарности следует, что
β’(c0 - cп) = kcп и cп = β’с0/(β’ + k).
(XVIII.11)
Отсюда
ω = [kβ′/(β′ + k)]c0.
(XVIII.12)
Если обозначить соотношение kβ′/(β′ + k) через β
, то
ω = β
c0.
(XVIII.13)
Очевидно, между величинами суммарного сопротивления β
, β′ и
k существует соотношение
1.β
= (1/β’) + (1/k).
(XVIII.14)
Таким образом, суммарное сопротивление складывается из диффузионного и химического. Предположим сначала, что β′ ≪ k. Это означает, что в уравнении (XVIII.14) можно пренебречь величиной 1/k по сравнению с 1/β′ и β
= β′, т.е. процесс идет в диффузионной области.
В этом случае, как следует из уравнения (XVIII.11), сп намного меньше с0 (стремится к нулю), т.е. имеет место градиент концентрации углерода в металле. Если же, наоборот, k ≪ β, то суммарная скорость определяется скоростью химической реакции. В этом случае из уравнения (XVII 1.11).следует, что cп = с0 и, следовательно, отсутствует градиент концентрации углерода. Попутно отметим, что рассмотренная химическая реакция сама является сложным процессом и представляет собой совокупность ряда элементарных актов, включающих адсорбцию молекул водорода на поверхности железа, образование на ней промежуточных радикалов - СН, СН2, СН3 и, наконец, метана, который десорбируется с поверхности.
Рассмотрим соотношение между суммарными и частными сопротивлениями при протекании процессов с параллельно идущими стадиями. Схематически пример процесса с тремя параллельными стадиями представлен на рис. XVIII.2.
Очевидно, в этом случае суммарный поток определяется уравнением:
П = β
c0 + β
c0 + β
c0
и, следовательно:
β
= β
+ β
+ β
.
(XVIII.15)
Таким образом, в процессах с параллельно протекающими стадиями общая проводимость равна сумме проводимостей
473
отдельных процессов. Если величины β
, β
, β
... очень отличаются друг от друга, то скорость процесса будет определяться скоростью наиболее быстро протекающего процесса.
Из сказанного следует, что первая задача при изучении кинетики сложных процессов - установление лимитирующих стадий.
474
