Ниже излагается теория цепных процессов, данная Н.Н. Семеновым. Сначала для реакций с неразветвляющимися цепями рассмотрим случай, когда возбудитель цепей присутствует в течение всего процесса и обеспечивает возникновение n0 центров за 1 с во всем объеме реакционного сосуда. Обозначим через τ среднее время жизни активного центра. Через τ секунд после возникновения активный центр либо погибает, либо порождает в результате реакции другой активный центр (или радикал). Обозначим через α вероятность продолжения цепи, а через β - вероятность гибели центра. Очевидно, α + β = 1. Если к моменту времени t в сосуде находится п центров, то скорость увеличения их числа определяется уравнением
dn/dt = n0 - (nβ/τ).
(XVII.2)
Очевидно, второй член правой части уравнения равен числу гибнущих в единицу времени центров, а продолжение цепи не увеличивает числа центров. Для того чтобы найти зависимость числа п от времени, следует проинтегрировать уравнение (XVII.2):
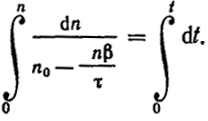
Учитывая, что d(n0 -
) = -
d
n, найдем, что
461
ln
=
t
ИЛИ
= e
-βt/τ
и
n =
(1 - e-βt/τ).
(XVII.3)
Графически зависимость n = f(t) представлена на рис. XVII.2.
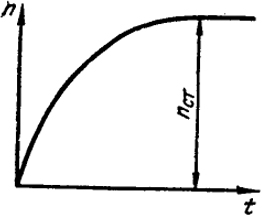
Рис. XVII.2. Зависимость числа центров от времени

Рис. XVII.3. Зависимость ω от τ при цепной взрыве
При t → ∞ возникает стационарное состояние, при котором nст = n0(τ/β), как это следует из уравнения (XVII.3).
Очевидно, при стационарном течении процесса dn/dτ = 0 и число возникающих центров равно числу гибнущих центров. При этом скорость процесса определяется соотношением
ωст = nст/τ = n0/β.
(XVII.4)
В соответствии со сказанным 1/β - длина цепи.
В начале предыдущей главы приводилось кинетическое уравнение для реакции образования НВr:
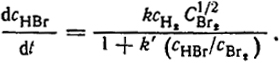
Это уравнение было найдено эмпирическим путем. Позднее оно было выведено при помощи теории цепных реакций
462
на основе предположения о следующем механизме реакции:
Br2
2Br;
(1)
Br + H2
HBr + H;
(2)
H + Br2
HBr + Br;
(3)
H + HBr
H2 + Br;
(4)
2Br
Br2,
(5)
где k1, k2, k3, k4, k5 - константы скорости.
Скорость образования HBr в этом случае определится уравнением
dcHBr/dt = k2cBrcH2 + k3cHcBr2 - k4cHcHBr.
(XVII.6)
Для получения кинетического уравнения, которое можно было бы сопоставлять с экспериментальными данными, из уравнения (XVII.6) следует исключить непосредственно не измеряемые величины концентраций атомарных водорода и брома. В связи с тем, что концентрация свободных атомов очень мала, в цепных реакциях быстро наступает стационарное состояние, при котором число центров (атомов), возникающих в единицу времени, равно числу центров, гибнущих в результате реакции. Так, атомы водорода, возникающие в реакции (2), полностью исчезают при реакциях (3) и (4) и, следовательно:
k2cBrcH2 = k3cHcBr2 - k4cHcHBr.
(XVII.7)
Подобным же образом атомы брома, образующиеся при реакциях (1), (3) и (4), исчезают при реакциях (2) и (5):
k1Br2 + k3cHcBr2 + k4cHcHBr = k2cBrcH2 + k5c
.
(XVII.8)
Вычитая из уравнения (XVII.8) уравнение (XVII.7), найдем, что
k1cBr2 = k5c
или
cBr =
√(k1/k5)cBr2.
Подставляя это значение cBr в уравнение (XVII.7), находим
cH =
| k2cH2√(k1/k5)cBr2 |
| k3cBr2 + k4cHBr |
.
463
Если теперь значения cBr и сH подставить в уравнение (XVII.6), то получим искомое кинетическое уравнение:
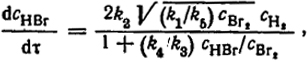
которое тождественно по форме уравнению (XV1I.6).
В случае разветвленных цепей активный центр, входя в реакцию, воссоздается в виде двух, трех или более новых центров, как это изображено на схеме:
Такое размножение активных центров является причиной цепных взрывов. Рассмотрим кинетику реакций с разветвляющимися цепями. Вследствие разветвления цепей число активных центров возрастает быстрее, чем в реакциях с простыми цепями. Если обозначить через δ вероятность разветвления, то, учитывая происходящее при этом увеличение числа центров, получим вместо уравнения (XVII.2)
dn/dt = n0 - (nβ/τ) + (nδ/τ).
(XVII.9)
Следует отметить, что, строго говоря, величина б не только представляет собой вероятность, но и содержит коэффициент разветвления (Р - 1), где Р - число ответвлений.
Н.Н. Семенов показал, что для большинства цепей коэффициент разветвления равен единице. Представляя уравнение (XVII.9) в виде
dn/dt = n0 - (n/τ)(β - δ)
и интегрируя подобно уравнению (XVII.2), найдем:
n =
[1 - et/τ(β - δ)].
(XVII.10)
Проанализируем это уравнение для частных случаев.
1. Пусть β > δ. В этом случае по истечении некоторого
464
времени (t → ∞) процесс примет стационарный характер со скоростью
ωст = n0/(β - δ).
(XVII.11)
Таким образом, при условии β > δ и при реакциях с разветвляющимися цепями может установиться стационарное течение процесса.
Из уравнения (XVII.11) следует, что дробь 1/(β - δ) имеет смысл длины цепи.
2. Если δ > β, то скорость неограниченно увеличивается со временем. Для удобства рассмотрения этого случая изменим в уравнении (XVII.10) знаки на обратные:
n =
[e
(t/τ)(δ - β) - 1].
Отсюда следует, что при t → ∞ число центров п → ∞ , т.е. с течением времени оно неограниченно увеличивается по экспоненциальному закону, и реакция должна принимать взрывной характер (цепной взрыв). Развитие реакции в этом случае графически представлено на рис. XVII.3.
Из рис. XVII.3 видно, что сначала процесс практически не развивается (индукционный период). В течение индукционного периода реакция в действительности происходит, однако с очень малой скоростью, и количество ее продуктов трудно определить с достаточной точностью. Поэтому точность определения величины индукционного периода зависит от чувствительности используемых методов анализа. В течение индукционного периода происходит накопление активных центров.
Каковы условия перехода стационарного течения реакции с разветвляющимися цепями к взрыву? Очевидно, эта граница определяется равенством δ = β. Величина β может быть изменена путем изменения условий протекания реакции. Как уже указывалось, цепи обрываются на стенках сосуда. При низких давлениях (β > δ) процесс имеет стационарный характер. Соотношение между β и δ зависит также от диаметра реакционного сосуда, поскольку от этой величины зависит отношение объема газовой смеси к поверхности стенок. Очевидно, чем больше диаметр, тем меньше вероятность обрыва цепей. Н.Н. Семенов нашел, что при прочих равных условиях скорость цепной реакции пропорциональна квадрату диаметра сосуда.
При повышении давления или добавлении инертных газов вероятность обрыва цепей на стенках уменьшается
465
и при достижении некоторого давления, когда β = δ, происходит переход в область взрывных реакций.
Как уже отмечалось при рассмотрении неразветвляющихся цепных реакций, р может быть увеличена путем добавления, к реакционной смеси порошков, адсорбирующих активные центры. Это должно приводить к уменьшению возможности взрыва. Наоборот, если покрыть стенки реакционного сосуда инертными веществами (например, парафином), уменьшающими адсорбцию активных центров, то создаются условия, благоприятствующие взрывному развитию реакции. Вообще величины пределов взрыва зависят от материала реакционного сосуда. Так, для реакции соединения водорода и кислорода в стальном сосуде нижний предел взрыва составляет 7 мм рт. ст., а в случае, если стенки сосуда покрыты Cr2O3, он повышается до 20 мм.
Н.Н. Семеновым была также разработана теория тепловых взрывов. В большом числе случаев газовые реакции протекают в условиях, близких к стационарным. Это определяется тем, что скорость выделения тепла при таких реакциях равна скорости его отвода в окружающую среду. В случае взрывных реакций скорость выделения тепла q1 больше скорости его отвода q2. Такое увеличивающееся саморазогревание смеси и самоускорение реакции приводят к тепловому взрыву. Рассмотрим, как будет изменяться соотношение между q1 и q2 в зависимости от температуры. Величина q1 равна произведению скорости реакции ω на ее тепловой эффект Q, т.е. q1 = ωQ. Например, для случая реакции второго порядка
q1 = ωQ = Qk∞e-E/RTc1c2.
(XVII.12)
Скорость теплоотвода при прочих равных условиях пропорциональна разности температур реакционной смеси Т и стенок сосуда Т0, т.е.
q2 = k’(T - T0).
(XVII.13)
На рис. XVII.4 представлены три возможных случая расположения кривых q1 (1, 2, 3) относительно q2 (прямая линия) в зависимости от давления. Чем больше давление, тем выше кривая (так как при большем давлении больше концентрации реагирующих компонентов).
При достаточно высоких давлениях (кривая 3) q > q2, и поэтому происходит тепловой взрыв. При достаточно низких давлениях (кривая 3) до T = T1 существует неравенство q1 > q2.
466
В этой области скорость реакции будет возрастать, пока не будет достигнута некоторая температура Т1, где q1 = q2 и разогревание прекратится, а следовательно, прекратится и ускорение реакции. Представленный кривой 2 случай соответствует пределу, при котором медленная реакция переходит во взрыв.
Из сказанного следует, что при любой температуре стенок сосуда T0 существует нижний предел тепловых взрывов. Наоборот, всякому давлению смеси соответствует определенная
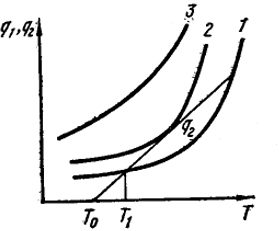
Рис. XVII.4. Схема расположения кривых выделения тепла
температура зажигания. В отличие от цепных взрывов для тепловых взрывов отсутствует верхний предел. В случае, представленном кривой 3, скорость выделения тепла всегда больше скорости его отвода, и поэтому скорость реакции должна неограниченно возрастать так, что начавшийся процесс заканчивается взрывом.
467
