§ 3. Теория переходного состояния

Всякая химическая реакция или любой другой молекулярный процесс, протекающий во времени (диффузия, вязкое течение), состоит в непрерывном изменении расстояний между ядрами атомов. При этом конфигурация ядер, отвечающая начальному состоянию, через некоторую промежуточную конфигурацию - активированный комплекс или переходное состояние - превращается в конечную конфигурацию. Например, при реакции диссоциации HI такой активированный комплекс образуется благодаря перегруппировке связей между атомами:

В разработанной Г. Эйрингом и М. Поляни теории переходного состояния принимается, что исходные вещества находятся в равновесии с активированными комплексами, т.е. скорость образования последних намного больше скорости их распада, и что распределение молекул реагирующих веществ по энергиям вследствие столкновений соответствует равновесному распределению Максвелла - Больцмана. Это равновесие рассчитывается при помощи методов статистической термодинамики. Переходное состояние (активированный комплекс) можно рассматривать как обыкновенную молекулу, характеризующуюся определенными термодинамическими свойствами, за исключением того, что, кроме обычных трех степеней свободы поступательного движения центра тяжести, оно имеет четвертую степень свободы внутреннего поступательного движения, связанную с движением вдоль пути (координаты) реакции.

Как отмечалось в гл. XI, § 5, молекула может иметь только 3r степеней свободы, если она состоит из r атомов. Поэтому переходное состояние, имеющее одну дополнительную степень свободы поступательного движения, должно

439

иметь на одну степень свободы колебательного движения меньше, чем обычная молекула с таким же числом атомов. Иными словами, одна внутренняя степень свободы колебательного движения переходного состояния превращается в степень свободы внутреннего поступательного движения вдоль координаты реакции. Вместе с тем переходное состояние не есть некоторое промежуточное соединение, так как ему соответствует максимальная энергия по пути реакции и, следовательно, оно неустойчиво и должно превращаться в продукты реакции.

Рассмотрим в общем виде реакцию А + В ←→ Х

*

*

  → С + D, где А и В - исходные вещества; X

*

*

 - переходное состояние, или активированный комплекс; С и D - продукты реакции.

Вследствие большой скорости образования переходного состояния оно находится в равновесии с исходными веществами А и В. Таким образом, рассматриваемая реакция состоит из двух последовательных процессов. Первый - это переход A и B в активированное состояние и второй - распад образовавшегося комплекса на продукты С и D. Скорость суммарной реакции ω определяется наиболее медленным звеном. Здесь таким звеном является переход комплекса Х

*

*

  через "плато" П. При этом, имеется в виду не скорость движения переходного состояния в пространстве, а движение точки, отображающей энергию системы. Будем называть переходным такое состояние, которое представлено точками, лежащими на вершине потенциального барьера на некотором малом отрезке δ на пути реакции. Заметим, что величина δ не будет фигурировать в конечных результатах.

Обозначим концентрацию переходных состояний в 1 см³ через с

*

*

  , а среднее время жизни переходного состояния на вершине барьера τ. Очевидно, скорость реакции определяется числом распадов всех переходных состояний в единице объема в единицу времени:

ω = c

*

*

  /τ. (XVI.27)

Величина τ может быть выражена через среднюю скорость движения переходного состояния и вдоль пути реакции на вершине барьера:

τ = δ/u. (XVI.28)

440

Средняя скорость одномерного движения, как обычно, определяется соотношением

где η - приведенная масса, отвечающая относительному движению отображающей точки по пути реакции. После интегрирования получим:

(XVI.29)

Отсюда

τ = δ√(2kT)/πη. (XVI.30)

Так как переходное состояние находится в равновесии с исходными веществами, то для нахождения его концентрации можно использовать закон действующих масс:

c

*

*

  /c_Ac_B = K

*

1

  , (XVI.31)

где К

*

1

  - константа равновесия процесса активации.

A + B ←→ X

*

*

  .

Так как концентрация переходных состояний пропорциональна δ, то и константа равновесия должна быть пропорциональна δ. Отсюда

c

*

X*

  = K

*

1

  c_Ac_B (XVI.32)

Подставляя величину τ из уравнения (XVI.30) и c

*

X*

  из уравнения (XVI.32) в уравнение (XVI.27), получим

ω = K

*

1

  c_Ac_B√2kT/πη. (XVI.33)

Сопоставляя уравнение (XVI.33) с уравнением для бимолекулярной реакции, мы видим, что константа скорости, которую для отличия от постоянной Больцмана обозначим здесь через k_r, непосредственно связана с константой равновесия процесса активации уравнением:

k_r = K

*

1

  √2kT/πη. (XVI.34)

Таким образом, в теории переходного состояния устанавливается связь между кинетическими и термодинамичесними

441

величинами. Величина K

*

1

  , как было показано в гл.

XIII для стандартного состояния одна молекула в 1 см³ может быть выражена при помощи соответствующих функций распределения Р:

(XVI.35)

Выше уже отмечалось, что переходное состояние можно рассматривать как обычную молекулу, в которой одна степень свободы колебательного движения заменена степенью свободы поступательного движения. Поэтому функцию распределения для переходного состояния можно выразить как произведение двух функций распределения Р^* обычной молекулы без одной степени свободы колебательного движения и P_пост - частицы с одной степенью свободы поступательного движения:

P

*

X*

  = P^*P_пост.

Известно, что Р_пост = √2πηkT/h. Однако при выводе этой формулы учитывалось движение частицы в обоих направлениях вдоль линии. Между тем в переходном состоянии отображающая точка движется только в положительном направлении. Поэтому число состояний, отвечающих переходному состоянию (п. с.), будет в два раза меньше, и, следовательно:

P_{пост.п.с} =

1

2

 

√2πηkT

h

Подставляя этот результат в уравнение (XVI.35), а затем в (XVI.33), получим:

(XVI.36)

или для константы скорости

(VXI.37)

Величина

P*

PAPB

  e^-E/RT - константа равновесия (K₂) процесса образования переходного состояния, рассматриваемое как обычная молекула без одной степени свободы

442

колебательного движения. Учитывая это, уравнение (XVI.37) можно переписать в виде

K_r =

kT

h

  K

*

2

  . (XVI.38)

Следовательно, множитель kT/h, как бы представляющий собой частоту распада переходного состояния, одинаков для всех реакций и зависит только от температуры. В целом уравнение (XVI.38) является совершенно общим для всех типов реакций - не только гомогенных, но и гетерогенных.

Изложенное выше показывает, что теория переходного состояния в отличие от теории столкновений позволяет в принципе вычислить величину предэкспоненциального множителя в уравнении для константы скорости. Поэтому эту теорию часто называют теорией абсолютных скоростей реакций.

Как видно из уравнения (XVI.37), для вычисления абсолютных скоростей реакций необходимо знание функций распределения исходных веществ и переходного состояния, определенных методами статистической термодинамики на основе спектроскопических данных. Величина функции распределения для переходного состояния может быть найдена, если известна поверхность потенциальной энергии.

Полученные соотношения позволяют выразить скорость процесса через термодинамические характеристики переходного состояния. Энергия Гиббса процесса активации определяется уравнением:

ΔG^0* = -RTlnK

*

2

  . (XVI.39)

Учитывая, что ΔG^0* = ΔH^0* - TΔS^0*, и, следовательно, K

*

2

  = e^-ΔH0*/RT e^ΔS0*/R, найдем из уравнения (XVI.38), что

k_r =

kT

h

  e^-ΔH0*/RT e^ΔS0*/R, (XVI.40)

где ΔH^0* и ΔS^0* - соответственно стандартные энтальпия и энтропия активации.

Из этого уравнения видно, что скорость реакции определяется не энтальпией активации, а изменением стандартной энергии Гиббса при этом процессе. Кроме того, из уравнения (XVI.40) следует, что предэкспоненциальный. множитель, или фактор частоты, непосредственно определяется изменением энтропии при активации.

443

В качестве примера рассмотрим мономолекулярную реакцию диссоциации двухатомной молекулы:

AB ←→ A - B → A + B

Переходное состояние

 

Учитывая, что консганта равновесия образования переходного состояния в этом случае

K^* =

cA - B

cAB

  =

P * A - B

PAB

  e^-E/RT,

где P

*

A - B

  и P_AB - соответственно функции распределения переходного состояния и исходной молекулы, и повторяя рассуждения, которые привели к уравнению (XVI.35), получим:

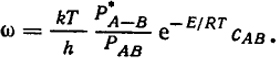(XVI.41)

Из этого уравнения видно, что если скорость реакции действительно определяется скоростью распада переходного состояния как наиболее медленного процесса, то эта реакция должна иметь первый порядок. Если переходное состояние представляло бы собой комплекс из двух молекул, то реакция имела бы второй порядок.

В рассматриваемой реакции переходное состояние отличается от исходного только следующим. Как отмечалось выше, колебание по разрываемой связи в переходном состоянии заменено внутренней поступательной степенью свободы вдоль координаты реакции. Это обстоятельство учтено в уравнении (XVI.35) и соответственно должно быть учтено в уравнении (XVI.41). Поэтому из величины Р_{A - B} в уравнении (XVI.41) следует исключить функцию распределения для одной степени свободы колебательного движения, а именно Р_кол = (1 - е^-hν/kT)^-1, т.е. P

*

A - B

  должна быть заменена отношением

PAB

(1 - e-hν/kT)-1

  .

Таким образом, уравнение (XVI.41) примет вид

ω =

kT

h

  (1 - e^-hν/kT)e-E/RTc_AB. (XVI.42)

Это уравнение удовлетворительно описывает кинетику мономолекулярных реакций. При высоких температурах, когда kT ≫ hν, величина(1 - е^-hν/kT) стремится к hν/kT (это можно показать, разлагая в ряд (e^-hν/kT), и, следовательно:

444

ω = νe^-E/RTc_AB и k = νe^-E/RT.

Таким образом, теория переходного состояния показывает, что предэкспонечциальный множитель в выражении для константы скорости мономолекулярных реакций (при высоких температурах) имеет смысл частоты колебания по линии разрываемой связи.

Применим уравнение (XVI.36) для расчета скорости простейшей бимолекулярной реакции - взаимодействия двух атомов А и В. Здесь переходное состояние представляет собой линейную конфигурацию из двух атомов А - В. Это переходное состояние имеет три степени свободы поступательного движения и две степени свободы вращательного движения. Одна степень свободы колебательного движения заменена внутренним поступательным движением по пути реакции. Функция распределения переходного состояния в этом случае определяется уравнением:

P^* = P

*

пост

  P

*

вращ

  . (XVI.43)

Согласно уравнениям (XIII.5) и (XIII.7)

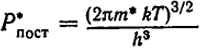и

где m^* и J^* - масса и момент инерции переходного состояния.

Очевидно, что m^* = m_A + m_B, где т_А и т_B - массы реагирующих атомов.

Приведенная масса переходного состояния, как уже указывалось, определяется уравнением:

μ = m_Am_B/(m_A + m_B).

Принимая, что радиус переходного состояния r^* = r_A + r_B, найдем момент инерции

J^* = μ(r^*)² =

mAmB

mA + mB

  (r_A + r_B)².

Подставляя все найденные выражения в уравнение (XVI.43), получим:

p^* =

[2π(mA + mB)kT]3/28π2mAmBkT(rA + rB)2

h3h2(mA + mB)

  .

Реагирующие атомы А и В имеют только поступательное движение и поэтому для них, согласно уравнению (XIII.5):

445

и

Подставляя найденные значения функций распределения в уравнение (XVI.36), получим:

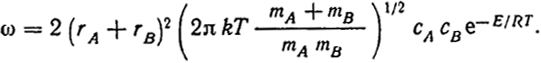(XVI.44)

Произведение, стоящее перед e^-E/RT, равно числу двойных столкновений:

Эта формула представляет собой точное выражение для числа сталкивающихся при двойных соударениях молекул. Для сложных бимолекулярных реакций теория переходного состояния позволяет вычислить величину стерического фактора. В частности, она объясняет причину аномально медленного протекания некоторых реакций с участием сложных молекул. Оценим величину стерического фактора для бимолекулярной реакции в общем случае, когда одна из реагирующих молекул А состоит из п_А атомов, а другая В - из п_B атомов. Так как мы хотим дать оценку величины стерического фактора независимо от природы реагирующих молекул, а учитывая лишь число атомов в них, то ограничимся определением порядка величины σ. При этом будем полагать равными функции распределения данного вида движения для всех реагентов. Составим таблицу для подсчета числа степеней свободы для реагирующей системы A + B ←→ п.с. (переходное состояние):

Как уже отмечалось, число колебательных степеней свободы в молекуле из п атомов равно 3n - 6; в переходном состоянии одна такая степень свободы переходит в поступательную степень свободы и поэтому для п. с. соответствующее

446

число равно 3(n_A + n_B) - 7. Подставляя функции распределения для A, B и п. с. в соответствующих степенях в уравнение (XVI.36), получим

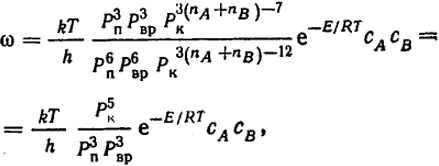(XVI.45)

где индексами "п", "вр" и "к" отмечены соответственно функции распределения поступательного, вращательного и колебательного движения.

Для оценки величины о применим теорию переходного состояния к бимолекулярной реакции A + В ←→ Х

*

*

  , принимая, что исходные молекулы и X

*

*

  подобны твердым шарам. В этом случае результат должен совпадать с теорией столкновений.

Здесь переходное состояние не имеет колебательного движения и одна из степеней свободы вращательного движения в переходном состоянии заменена степенью свободы движения вдоль координаты реакции, следовательно:

(XVI.46)

Введя стерический фактор σ, получим

(XVI.47)

Сопоставляя уравнения (XVI.47) и (XVI.45), находим что

σ = (

Pк

Pвр

)⁵.

Таким образом, теория переходного состояния показывает, что малая величина стерического фактора, обусловливающая аномально медленное протекание некоторых реакций, определяется тем, что при образований переходного состояния происходит замена вращательных степеней свободы колебательными. Вероятность вращательного движения, как это следует из величин функций распределения, больше, чем колебательного. При обычных температурах Р_к близка к единице, P_вр колеблется в пределах от 10 до

447

100. Следовательно, стерический фактор в реакциях с участием сложных молекул изменяется от 10^-5 до 10^-10 и определяется не геометрической вероятностью, как это предполагали ранее. В частности, он зависит от вероятности определенного согласования вращательного движения реагирующих молекул. Стерический фактор, таким образом, отражает не статическое положение молекул в пространстве, а динамические процессы.

Теория переходного состояния имеет важное значение не только для кинетики гомогенных реакций, но и для значительно более широкого круга физико-химических явлений. В частности, она применима для анализа процесса диффузии в твердых телах и жидкостях.

Коэффициент диффузии в веществах имеющих кубическую решетку, определяется соотношением:

D = α(d²/τ), (XVI.48)

где d - постоянная решетки; α - геометрический фактор; τ - среднее время между двумя последовательными прыжками диффундирующего атома.

Будем рассматривать акт диффузии как мономолекулярный процесс. Тогда число таких актов в единице объема в единицу времени составит (1/τ)с(с - концентрация диффундирующего вещества). Величина 1/τ имеет смысл константы скорости. Таким образом, в соответствии с основным уравнением (XVI.38):

1/τ = (kT/h)K^* (XVI.49)

Атом, колеблющийся около своего положения равновесия, может с одинаковой вероятностью переместиться в нескольких различных эквивалентных направлениях р. Так, например, для диффузии в твердых металлах по междоузлиям р = 4 в объемноцентрированной решетке и р = 12 - в гранецентрированной. В связи с этим константа скорости увеличится в р раз и вместо уравнения (XVI.49) получим

1/τ = p(kT/h)K^*. (XVI.50)

Ранее было показано, что K^* = P^*/Pe^-E/RT. При рассмотрении мономолекулярных реакций мы приняли, что P^* =

P

kT

  /hν. Однако в случае диффузии нельзя считать, что переходное состояние отличается от исходного лишь отсутствием одной степени свободы. Это обусловлено, в частности, тем, что в твердом теле переход атома в промежуточное

448

положение вызывает смещение других атомов в решетке. Поэтому Р^* =

P’

kT/hν

  , и таким образом:

1/τ = pν(P’/P)e^-E/RT. (XVI.51)

Рассмотрим изменение энергии Гиббса ΔG⁰ при переходе из исходного состояния (характеризуемого функцией распределения Р) в переходное (характеризуемое функцией распределения Р’). При равновесии

K’ = (P’/P)e^-E/RT

или, так как

K’ = e^-ΔG0’/RT, то (P’/P)e^-E/RT = e^-ΔG0’/RT

Таким образом:

1/τ = pνe^-ΔG0’/RT = pνe^ΔS0’/Re^-ΔH0’/RT. (XVI.52)

Отсюда из уравнения (XVI.48) следует выражение для коэффициента диффузии:

D = pαd²νe^ΔS0’/Re^-ΔH0’/RT. (XVI.53)

Предэкспоненциальный множитель в этом уравнении, величина которого не зависит от температуры, обозначим через D₀ (гл. XIV, § 3):

D₀ = pαd²νe^ΔS0’/R. (XVI.54)

Часто уравнение (XVI.53) записывают сокращенно:

D = D₀e^-ΔH0’/RT.

Отсюда видно, что величина ΔH⁰’ соответствует экспериментально определяемой по температурной зависимости коэффициента диффузии D теплоте активации процесса диффузии.

Для оценки величины ΔS⁰’ допустим, что все изменение энергии Гиббса активации определяется упругой энергией, возникающей в кристаллической решетке, когда диффундирующий атом переходит на вершину потенциального барьера, т.е.

ΔG⁰’ = 1/2μl²V, (XVI.55)

где μ - модуль сдвига решетки; l - деформация сдвига; V - объем, в котором локализована деформация.

449

Опыт показывает, что модуль сдвига линейно зависит от температуры, т.е. μ = μ₀ + T(∂μ/∂T). Подставляя это выражение в уравнение (XVI.55), найдем, что

ΔG⁰’ = 1/2μ₀l²V + T

l2V

2

 

∂μ

∂T

  .

Сопоставляя это с термодинамическим уравнением ΔG⁰’ = ΔH⁰ - TΔS⁰, видим, что

ΔH⁰’ = 1/2μ₀l²V и ΔS⁰’ =

l2V

2

 

∂μ

∂T

  = -

ΔH0’

μ0

 

∂μ

∂T

  . (XVI.56)

Так как величина μ уменьшается с ростом температуры, то энтропия активации - положительная величина и е^ΔG0’/R > 1. Полученные соотношения были сопоставлены с экспериментальными данными. Для этой цели в уравнение (XVI.54) подставляли известные величины р, α, ν и d² и по экспериментальным данным вычисляли значения ΔS⁰’, которые сравнивали с найденными из уравнения (XVI.56). Результаты такого сопоставления показали хорошее соответствие между экспериментальными значениями ΔS⁰’ и величинами, найденными на основе теории. Особенно хорошее соответствие наблюдалось для случая диффузии углерода в α-Fe, где получены наиболее точные данные.

450