Накопление опытных данных по кинетике химических реакций дало возможность развить теоретические представления в этой области. С. Аррениусом была разработана
427
теория активных столкновений для бимолекулярных реакций второго порядка, основанная на использовании кинетической теории газов.
Рассмотрим кинетику реакции Н2г + I2г = 2НIг.
Так как эта реакция является бимолекулярной, но она должна осуществляться путем столкновений между молекулами. В связи с этим интересно сопоставить число столкновений z (за 1 с в 1 см3) молекул двух сортов с наблюдаемой скоростью реакции ω. Далее будет показано [уравнение (XVI.44)], что число двойных столкновений определяется формулой:
 (XVI.20)
(XVI.20)
где п1 и п2 - числа молекул первого и второго сортов в 1 см3; k - постоянная Больцмана; μ =
- приведенная масса сталкивающихся молекул в случае столкновения двух молекул
А и
В с массами
mA и
mB,
r - сумма радиусов этих молекул, т.е.
r =
rA +
rB.
Допустим, что все такие двойные столкновения приводят к реакции, т.е. что предположение о равенстве z = ω правильно. Легко подсчитать, что в этом случае, например для реакции 2HIг → H2г + I2г при 700 К и атмосферном давлении, число соударений в 1 см3 за 1 с составляет величину порядка 1028 и, следовательно, скорость реакции была бы чрезвычайно большой - она завершалась бы за 10-10 с. Между тем наблюдаемая в действительности скорость диссоциации HI на много порядков меньше. Такое несоответствие между вычисленной и наблюдаемой скоростями реакции должно было привести к заключению, что не каждое столкновение молекул является эффективным, т.е. заканчивается реакцией.
Первоначально было предположено, что элементарный акт реакции осуществляется лишь в тех случаях, когда сталкивающиеся частицы определенным выгодным образом ориентированы друг относительно друга в пространстве. В соответствии с этим было введено представление о стерическом факторе или о так называемой геометрической вероятности σ. Этот фактор указывает величину вероятности благоприятных в геометрическом отношении столкновений и, таким образом, ω = σz.
Однако это предположение не объясняет опытных данных. Во-первых, оно не согласуется с наблюдаемой в действительности сильной зависимостью скорости реакции от
428
температуры (k = k∞e-E/RT), поскольку z сравнительно слабо зависит от температуры (пропорционально √Т). Во-вторых, для согласования экспериментальных данных с расчетными пришлось бы принять величину σ равной 10-14 - 10-15.
Очевидно, геометрическая вероятность не может быть столь малой величиной. Выдвинутая в связи с этим Аррениусом идея состояла в том, что условием реакции является не особое геометрическое положение сталкивающихся молекул друг относительно друга, а повышенный запас их энергии.1 Он предположил, что любая реакция осуществляется через промежуточное состояние, которое связано с возникновением "активных" молекул, образующихся из "нормальных" молекул в результате столкновений. Такая схема сохранилась в основе современных представлений о механизме химических превращений.
Избыточная энергия, необходимая для того, чтобы произошла реакция, не равна сумме энергий сталкивающихся активных молекул. При оценке этой энергии следует учитывать лишь ту ее часть, которая зависит от составляющих скоростей, соответствующих относительному движению вдоль линии столкновения. Такой линией называется прямая, соединяющая центры тяжести сталкивающихся молекул.
На рис. XVI.6 представлена простейшая модель молекул как жестких шаров, а их скорости в момент столкновения u1 и u2 разложены на составляющие вдоль линии центров и перпендикулярные к ней.
Очевидно, что взаимодействие сталкивающихся молекул совершенно не зависит от абсолютной скорости движения центра тяжести системы молекул. Фактором, который определяет эффективность столкновения, является лишь кинетическая энергия движения реагирующих молекул друг относительно друга. Это движение может быть описано (см. гл. XII) как движение одной точки, имеющей массу, равную приведенной массе, и скорость, равную относительной скорости. Энергия этой точки равняется сумме энергий движения молекул по линии центров.
Для того чтобы реакция произошла, необходимо, чтобы энергия относительного движения по линии столкновения превысила некоторую критическую величину, т.е. энергию активации ? (в расчете на один моль). Если обозначить
429
через η (E) вероятность того, что эта энергия будет равна или больше Е, то скорость реакции выразится уравнением
ω = σzη(E) = 2σ(2πkT/μ)1/2r2n1n2μ(E).
(XVI.21)
Поскольку, как будет показано ниже, а близка к единице, то можно считать, что главным фактором, определяющим скорость реакции, наряду с z является η(E). Величина η(E) может быть найдена при помощи закона распределения Больцмана. Так как энергия движения точки с приведенной массой μ равна сумме энергий относительного движения сталкивающихся молекул, то эта энергия содержит два квадратичных члена.
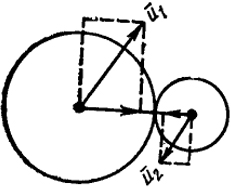
Рис. XVI.6. Двойное соударение молекул
Как было показано в гл. XI, доля молекул, имеющих энергию E или больше E, в случае двух квадратичных членов равна e-E/RT, т.е. η(E) = e-E/RT. Подставляя это значение η(E) в уравнение (XVI.21), получим:
ω = σze-E/RT = 2σ(2πkT/μ)1/2r2n1n2e-E/RT.
(XVI.22)
Так как для бимолекулярной реакции ω = kc1c2 или в данном случае, когда концентрации выражены в числах молекул в 1 см3, ω = kn1n2, то из уравнения (XVI.22) следует:
k = 2σr2(2πkT/μ)1/2e-E/RT.
(XVI.23)
Логарифмирование этого выражения дает
ln k = -(E/RT) + 1/2 ln T + ln A,
(XVI.24)
где А - постоянная, включающая r, постоянную Больцмана k, μ и σ.
Сопоставление уравнений (XVI.19) и (XVI.24) показывает, что теория столкновений в общем удовлетворительно объясняет наблюдаемую на опыте зависимость константы скорости от температуры, поскольку величина ln Т сравнительно слабо зависит от температуры.
Следует отметить, что величина e-E/RT, как правило, весьма мала, и, следовательно, лишь небольшая часть столкновений приводит к реакции. Например, если величина Е составляет 192000 Дж, как это наблюдается для диссоциации HI, то при 500 К
e-192000/8,314·500 = 10-20.
430
При повышении температуры доля эффективных столкновений быстро увеличивается. Так, при 1000 К e-192000/8,314·1000 = 10-10, т.е. возрастает на десять порядков при увеличении температуры на 500°.
Количественная проверка изложенной выше теории столкновений может быть осуществлена путем сопоставления величины энергии активации, вычисляемой из уравнения (XVI.23), со значением, определяемым из опыта по температурной зависимости константы скорости.
Радиусы реагирующих молекул находят из результатов измерения вязкости или рефракции (см. главы XIV и XXIV). Приведем пример такого сопоставления. Для реакции диссоциации йодистого водорода HI + HI → H2 + I2 экспериментально найденная энергия активации составляет 192000 Дж. При 556 К константа скорости составляет 3,5·10-7 л·моль-1·с-1.
Учитывая эту размерность константы скорости при определении числа столкновений молекул, в уравнении (XVL20) и соответственно (XVI.23) вместо концентраций, выраженных в числах молекул в 1 см3, следует подставить концентрацию в молях на литр. Для этого примем во внимание, что c =
=
(в данном случае
с1 =
c2 =
с и
n1 =
n2 =
n). Кроме того, для определения числа столкновений одинаковых молекул (HI) уравнение (XVI.20) следует разделить на 2, чтобы каждое столкновение не учитывать дважды. Отсюда число столкновений в 1 см
3
z = r2(
)
1/2 c1c2(
)
2.
Для того чтобы перейти от числа столкновений в 1 см3 к числу столкновений в 1 л и выразить эту величину в молях, умножим z на 1000 и разделим на 6,02·1023. Таким образом:
z’ = z2(
)
1/2c1c2(
).
Из данных о вязкости известно, что для йодистого водорода r = 3,5·10-8 см. Величина константы Больцмана k = 1,38·10-18 эрг/K
μ =
=
.
Подставляя приведенные значения в уравнение для k, получим:
431
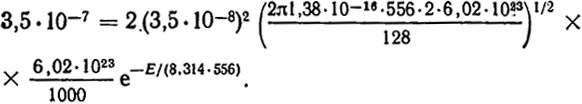
Расчет показывает, что E = 192000 Дж, т.е. находится в хорошем согласии с опытом. Из этого расчета следует, что величина а близка к единице. Подобная проверка, проведенная для других бимолекулярных реакций, показала, что в ряде случаев наблюдается удовлетворительное согласие с экспериментальными данными и, следовательно, величина σ мало отличается от единицы.
Вместе с тем было найдено много случаев так называемых медленных реакций в растворах, где скорости намного меньше, чем вычисляемые по уравнению (XVI.23). Например, Н.А. Меншуткиным была исследована кинетика реакций присоединения йодистого алкила к третичному амину типа N(C2H5)3 + (C2H5)I → N(C2H5)4I, в которых для согласования с опытом величину о пришлось бы принять равной 10-8.
Сначала полагали, что медленное протекание подобных реакций обусловлено дезактивацией реагирующих молекул вследствие столкновений с молекулами растворителя. Однако в дальнейшем было найдено, что эти реакции, если они осуществляются в газовой фазе, также протекают весьма медленно.
Таким образом, теория С. Аррениуса оказалась не в состоянии объяснить аномально медленное протекание ряда реакций. Эта неудача объясняется упрощенным характером теории, которая ограничивается чисто механическим рассмотрением столкновений между молекулами как упругими шарами и не учитывает степеней свободы, связанных с колебательными и вращательными движениями реагирующих молекул.
Так как обычно стерический фактор мало отличается от единицы, то скорость бимолекулярной реакции определяется в основном величиной энергии активации. Поэтому можно было бы ожидать, что такие реакции, для которых энергия активации близка к нулю (например, реакции рекомбинации атомов), должны протекать с большими скоростями. Однако в действительности такие реакции протекают со скоростями, значительно меньшими, чем вычисляемые по уравнению (XVI.23). Это противоречие объясняется тем, что вновь образовавшиеся молекулы обладают запасом энергии, представляющим собой сумму кинетической
432
энергии столкнувшихся атомов и теплоты реакции. Если такая молекула не сможет освободиться от избытка энергии сразу после соударения, то она вновь диссоциирует на атомы. Из-за закона сохранения импульса этот избыток энергии не может превратиться в кинетическую энергию образовавшейся молекулы.
Освобождение от избытка энергии в реакции, например, атомов водорода рекомбинации осуществляется благодаря тройным соударениям с участием какой-нибудь молекулы М : 2Н + М → Н2 + М*, где М* - молекула с повышенной энергией или атомы поверхности, на которой происходит столкновение. Эта особенность реакций рекомбинации использовалась в технике для бескислородной сварки. Предложенный И. Лангмюром метод состоит в том, что на поверхность металла направляется узкий пучок атомов водорода, рекомбинация которых приводит к большому выделению тепла и локальному плавлению металла на месте шва.
В химическом акте мономолекулярной реакции участвует одна молекула. К числу таких реакций относится ряд процессов термического распада сложных молекул, внутренней перестройки молекул (инверсия, изомеризация, рацемизация), например
N2O5 = 2NO2 + 1/2O2,
или

Порядок реакции, как уже отмечалось, может отличаться от ее молекулярности. Рассмотрим зависимость порядка мономолекулярной реакции от концентрации. Пусть общая концентрация молекул равна с, а концентрация активных молекул с*. Так как молекулы активируются в результате бинарных столкновений, то скорость активации ωа = kac2. Активированная молекула может либо прореагировать, превратившись в продукт реакции, либо дезактивироваться при соударении с инертной молекулой. Скорость химической реакции ωx = kxc*, а скорость дезактивации ωд = kдсс*.
433
При стационарном течении реакции число возникающих в единицу времени активных молекул равно их числу, которое исчезает как вследствие химического превращения, так и в результате дезактивации, т.е. kac2 = kxc* + kдcc*. Отсюда следует, что
c* = kac2/(kx + kдc)
и, следовательно, скорость реакции
ωx = kxc* = (kakxc2)/(kx + kдc).
При малых величинах с произведение kдc ≪ kx, т.е. кинетика реакции описывается уравнением второго порядка. При больших концентрациях kдc ≫ kx и ωx =
с выполняется уравнение для реакций первого порядка. В области промежуточных концентраций могут наблюдаться реакции с дробным порядком в пределах от 1 до 2. Естественно, что наблюдаемый порядок реакции зависит и от соотношения между величинами констант
kx и
kд.
Возникает вопрос о природе энергии активации в мономолекулярных реакциях. Активация молекул не может осуществляться в результате поглощения лучистой энергии хотя бы потому, что реагирующие вещества не поглощают света как раз в области тех длин волн, которые должны были бы вызывать активацию. Облучение светом с такими длинами волн не приводило к ускорению реакций. Позже возникла теория, согласно которой причиной превращения молекулы является миграция тепловой энергии. Для того чтобы произошла реакция, необходимо, чтобы определенная критическая энергия сконцентрировалась на той связи внутри молекулы, по которой происходит разрыв.
Таким образом, после активирующих столкновений возникают активные молекулы, обладающие избытком колебательной энергии. Эта колебательная энергия перераспределяется по связям внутри активной молекулы. Если на участвующей в реакции связи сосредоточится колебательная энергия, превышающая некоторую критическую величину (энергию активации), то происходит акт реакции.
Из сказанного следует, что в мономолекулярных реакциях молекулы получают избыточную энергию (энергию активации) вследствие столкновений. Отдельные связи внутри молекул можно рассматривать как статистические единицы, распределение энергии между которыми определяет долю эффективных колебаний, приводящих к реакции. При этом каждой связи соответствуют два квадратичных члена,
434
поскольку при колебании изменяется как кинетическая, так и потенциальная энергия (см. гл. XI. § 5).
Вероятность того, что энергия колебания вдоль данной связи вследствие соударений достигнет величины энергии активации E или превзойдет ее, составляет η(E) = e-E/RT. Если бы каждое колебание приводило к разрыву связи, то число актов реакции в единицу времени в 1 см3 было бы равно произведению из числа молекул с этом объеме на частоту колебания молекулы ν, т.е. скорость реакции была бы ω = cν. Однако в действительности не каждое колебание является результативным, поэтому при подсчете скорости реакции следует учитывать лишь долю эффективных колебаний, т.е.
ω = сνe-E/RT.
(XVI.25)
Это уравнение, как уже отмечалось, должно выполняться лишь при условии, что время между столкновениями молекул существенно меньше времени, необходимого для разрыва связи, т.е. при относительно больших концентрациях. Сопоставляя уравнение (XVI.25) с уравнением для скорости реакций первого порядка ω = kc, найдем, что
k = νe-E/RT.
(XVI.26)
Определяя по температурной зависимости k величину Е, можно вычислить ν при данной температуре. Найденные величины колеблются в пределах 1012 - 1014c-1, что находится в согласии с независимыми измерениями другими методами (см. гл. XXIV).
В рамках рассмотренной теории столкновений не ставился вопрос о физическом смысле энергии активации и ее связи со строением реагирующих молекул. Этой величине давалось лишь формальное определение. Предполагалось, что энергия активации необходима для разрыва сильных химических связей между атомами в молекулах. Поскольку при реакции эти связи должны быть разрушены, можно было бы ожидать, что величина энергии активации должна быть близка к энергии разрываемых связей. Однако это простое предположение не подтверждается опытом. Так, например, в реакции между атомом водорода и молекулой водорода при превращении параводорода в ортоводород
→
энергия активации составляет ∼25 кДж/моль, в то время как энергия разрываемой связи в молекуле водорода близка к 435 кДж/моль.
435
Эмпирически было установлено правило, согласно которому энергия активации в реакциях между атомом и молекулой составляет примерно 5,0 % от энергии разрываемых связей. Если такие реакции являются эндотермическими, то энергия активации составляет 5,0 % от энергии разрываемых связей плюс теплота реакции. Например, энергия связи в молекуле водорода равна 435 кДж, а энтальпия реакции
Brг + Н2г = НВrг + Нг
составляет 69,5 кДж/моль. Таким образом, сумма (435/100)5 + 69,5 = 91,25 кДж/моль близка к экспериментально наблюдаемой энергии активации, равной 73,6 кДж/моль.
При реакциях между молекулами, например, H2г + I2г = 2HIг энергия активации составляет часто ∼30 % от суммы энергий разрываемых связей. В подобных реакциях энергия активации, как правило, близка к энергии наиболее слабой из разрывающихся связей.
Несовпадение величин энергии активации и энергий разрываемых связей объясняется тем, что на самом деле активация молекулы не заключается в разрыве связи. Рассмотрим случай, когда атом дейтерия приближается к молекуле водорода по линии ее связи.
Если атом D приблизится к молекуле на расстояние, равное расстоянию между атомами в молекуле, то ввиду симметричности системы валентные электроны будут охватывать все три ядра.
Такая сложная атомная система может распасться с образованием новой молекулы HD, сопровождающейся уходом атома Н. Для того, чтобы подойти на достаточно близкое расстояние к молекуле H2 атому D необходимо преодолеть силы отталкивания, существующие между насыщенной молекулой и любой другой молекулой или атомом (см. гл. XXII) вследствие отталкивания электронных оболочек.
Это отталкивание уменьшается благодаря тому, что по мере приближения атома дейтерия расстояние между атомами водорода в молекуле увеличивается. Следовательно, для того, чтобы произошло столкновение частиц и последующая реакция, требуется затрата энергии. Эта энергия и есть энергия активации, необходимая для преодоления сил отталкивания между частицами.
В рассматриваемом случае вся энергия системы зависит от двух координат: расстояний Н - D и Н - Н. Вообще, если атом А приближается по линии связи к молекуле ВС, то
436
при реакции A + BC = AB + C энергия зависит от расстояний rAB и rBC.
Современная теоретическая физика позволяет оценивать энергию такой системы как функцию этих двух координат. Для большинства реакций можно полагать, что ядра движутся так медленно, что электроны успевают для каждой конфигурации ядер принять энергетически наиболее выгодное распределение (адиабатическое протекание реакции).
Так как энергия зависит от двух координат, то она может
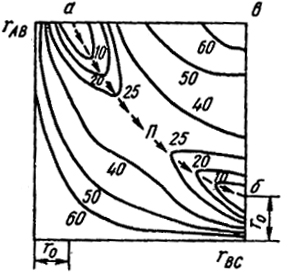
Рис. XVI.7. Диаграмма потенциальной энергии системы из трех атомов
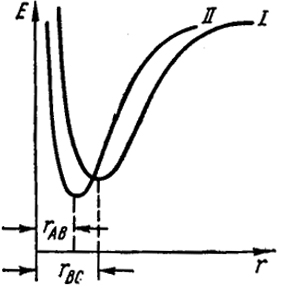
Рис. XVI.8. Зависимость потенциальной энергии от расстояния между атомами в молекулах
АВ и
ВС
быть изображена при помощи графика на плоскости. В рассматриваемой реакции атом А может приблизиться к молекуле ВС как по линии, являющейся продолжением линии, соединяющей центры атомов B и С, так и по перпендикулярному направлению. Очевидно, в первом случае затрата энергии на преодоление сил отталкивания будет меньше, так как атом А взаимодействует преимущественно только с одним атомом (В или С), а не одновременно с двумя. Поэтому наибольший интерес представляет случай, когда все три атома находятся на одной линии. На рис. XVI.7 для такого случая изображена диаграмма, на которой на оси абсцисс нанесены величины rBC, а на оси ординат rAB
Величину энергии, соответствующую данным rАВ и rBC, следовало бы наносить на третьей оси, перпендикулярной плоскости первых двух. При этом получилась бы пространственная диаграмма. Если же соединить, как это сделано
437
на рис. XVI.7, линиями точки с одинаковой энергией, то диаграмма даст представление о поверхности потенциальной энергии системы и будет подобна топографической карте. Цифры на кривых условно обозначают энергию или -высоту уровня. Видно, что перевал П лежит на "плато" между двумя высотами, отмеченными цифрой 25.
В качестве начального состояния принимается энергия системы: атом А - молекула ВС, т.е. rАВ = ∞ и rBC = ∞, где r0 - равновесное расстояние между ядрами в молекуле (точка а на рис. XVI.7).
Конечное состояние представляет собой новую молекулу АВ, от которой удален атом с, т.е. rAB = r
,
rBC = ∞ (точка
б). Точка
в соответствует энергии системы, когда три атома отделены друг от друга большими расстояниями, т.е.
rAB и
rBC очень велики. Сечения по горизонтальной линии
аб и вертикальной
вб (см. рис. XVI.7) представляют собой кривые потенциальных энергий двухатомных молекул
вс и
ав соответственно (кривые
I и
II на рис. XVI.8). Устойчивым состоянием этих молекул (точки
а и
б) отвечают минимумы потенциальной энергии. Из рис. XVI.8 видно, что конечное и начальное состояния лежат в двух "долинах", разделенных "перевалом" П. Здесь все три атома максимально сближены и образуют как бы одну молекулу. Реакция, т.е. движение системы, состоящей из трех атомов, из начального состояния в конечное соответствует переходу через этот перевал. Такой переход проходит по наиболее выгодному пути, т.
е. с наименьшей затратой энергии (наименьшей энергией активации). Он состоит в подъеме по "ущелью", движении через седлообразный "перевал" П и спуске также по "ущелью" в другую "долину". Этот путь, показанный на рис. XVI.7 стрелками, называется путем или координатой, реакции. Линии равной энергии на рис. XVI.7 справа и слева от пути реакции лежат на откосах "ущелий". Чем дальше они от этого пути, тем выше их положение на откосах ущелья.
Изменение энергии вдоль пути реакции было уже представлено на рис. XVI.4. "Перевал" или "седло", соответствует переходному состоянию, или активированному комплексу, в котором все реагирующие частицы наиболее сближены между собой. Б переходном состоянии система имеет максимальную потенциальную энергию на наиболее выгодном пути реакции. Эта максимальная энергия и есть энергия активации.
Таким образом, энергия активации приобретает смысл энергии переходного состояния. Для того чтобы произошла
438
реакция, энергия реагирующей системы должна позволить ей образовать переходное состояние. Вероятность осуществления реакции связывается, следовательно, с вероятностью образования переходного состояния. В результате возникает возможность применения статистических методов для расчета скорости процессов, которая реализуется в теории переходного состояния.
439
1
С. Аррениус первоначально предполагал, что активные молекулы представляют собой определенную химическую модификацию.
