Скоростью химической реакции ω называется скорость изменения концентрации какого-либо из участвующих в ней веществ. В гетерогенных реакциях, протекающих на поверхности пористых твердых тел, скорость реакции относят к единице массы или объема твердой фазы, а в случае жидких или твердых фаз при известной поверхности - к единице поверхности раздела. Величина ω имеет отрицательный или положительный знак в зависимости от того, исчезает или образуется вещество в ходе данной реакции. Для реакции aA + bB → gG + hH скорость может выражаться одной из следующих производных:
-
, -
, +
, +
,
где τ - время; cA, cB и cH - концентрации.
Величины этих производных связаны между собой стехиометрическими коэффициентами a, b, g и h.
Таким образом, по скорости изменения концентрации только одного из реагирующих веществ можно определять скорость изменения концентрации остальных реагентов. Скорость химической реакции есть функция концентраций реагирующих веществ и температуры, т.е. ω = f(с, Т).
Существуют два основных метода измерения скорости химических реакций: динамический и статический. Динамический метод может быть пояснен схемой, представленной на рис. XVI.1.
Смесь реагирующих веществ при низкой температуре подается в реакционную зону Р, где поддерживается достаточно высокая для протекания реакции постоянная температура Т. Необходимо, чтобы смесь из реакционной зоны выходила максимально быстро и вновь попадала в зону
417
с низкой температурой, где реакция практически прекращается, а смесь "закаливается". Производя анализ смеси до поступления в зону Р и после закалки и зная время пребывания смеси в реакционной зоне, определяют скорость реакции.
В статических методах проводятся измерения концентраций реагирующих веществ без непрерывного введения и выведения смеси из реакционной зоны. В одних случаях это достигается отбором быстро охлаждаемых проб, в других - при изучении реакций с участием газов путем изменений суммарного давления в смеси и парциальных давлений. Таким способом И. Лангмюр изучал, например, скорость реакции 2СОг + О2г = 2СO2г, проходившей на поверхности накаливаемой платиновой проволоки, помещенной в замкнутый стеклянный сосуд при общем давлении ∼4×10-2 Па. При таком низком давлении скорость диффузии очень велика и газовая фаза остается однородной во всем объеме, поэтому скорость реакции можно измерять чувствительным манометром по уменьшению общего давления.
Часто скорость реакции определяют путем измерений каких-либо физических свойств, зависящих от концентрации, например теплопроводности газовых смесей, угла вращения плоскости поляризации света в растворах, электропроводности и пр.
Гульдбергом и Вааге был сформулирован закон формальной кинетики, по которому (как это уже указывалось в гл. III) скорость прямой реакции A + 2B → AB2 определяется выражением
ω = -dcA/dτ = kcAc
,
(XVI.1)
где k - коэффициент пропорциональности или константа скорости реакции, которая также называется удельной скоростью реакции.
Величина k имеет смысл скорости реакции при концентрациях всех реагирующих веществ, равных единице.
Уравнения, подобные (XVI.1) и выражающие функциональную зависимость между скоростью реакции и концентрацией, называются кинетическими.
Порядком реакции называется сумма показателей степеней, в которых входят концентрации в кинетическое уравнение. Написанная выше реакция согласно этому определению является реакцией третьего порядка. В действительности же реакции третьего порядка встречаются очень редко, а реакции более высоких порядков вообще не наблюдаются.
418
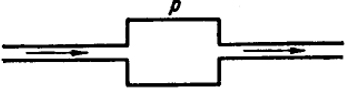
Рис. XVI.1. Схема динамического метода
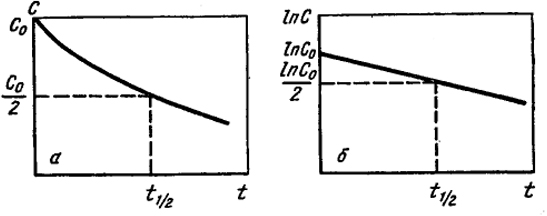
Рис. XVI.2. Изменение концентрации в зависимости от времени при протекании реакции первого порядка:
а - в координатах
с - τ;
б - в координатах ln
с - τ
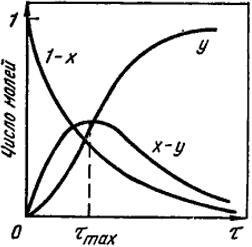
Рис. XVI.3. Изменение концентраций веществ при протекании последовательной реакции
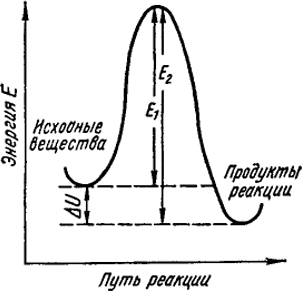
Рис. XVI.4. К понятию об энергии активации
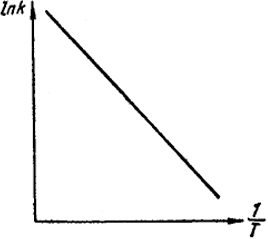
Рис. XVI.5. Зависимость логарифма константы скорости химической реакции от обратной абсолютной температуры
419
Следует отметить, что уравнения, подобные (XVI.1), были сформулированы на основе упрощенных представлений о том, что для реакции необходимы одновременные столкновения молекул реагентов в соответствии со стехиометрическим уравнением.
Уравнения типа (XVI.1) применимы лишь к элементарным актам и обычно не описывают суммарные реакции, которые почти всегда состоят из одного или более промежуточных процессов.
Часто реакции, подчиняющиеся простым кинетическим уравнениям, бывают нулевого, первого и второго порядка. На основании вида стехиометрического уравнения реакции еще нельзя сделать заключение о действительном механизме реакции. Например, реакция H2г + Br2г → 2HBrг подчиняется сложному кинетическому уравнению:
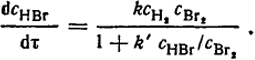
и не является реакцией второго порядка, как это можно было бы предположить, исходя из стехиометрического уравнения.
В связи с этим в кинетику наряду с понятием порядка реакции введено понятие молекулярное, т.е. числа частиц, действительно принимающих участие в элементарном акте реакции (в мономолекулярной - одна частица, в бимолекулярной - две). Таким образом, понятие порядка реакции эмпирическое, а молекулярности теоретическое.
В качестве иллюстрации отличия порядка реакции от молекулярности рассмотрим вопрос о том, какой порядок может иметь мономолекулярная реакция. Элементарным актом многих мономолекулярных реакций является распад молекулы, например диссоциация ацетона:
(СН3)2СОг = С2Н6г + СОг.
Сама по себе такая молекула устойчива. Прежде чем распасться, она должна приобрести избыток энергии благодаря столкновениям с другими молекулами, движущимися с большими скоростями, т.е. должна быть активирована. Это означает, что реакция идет в две стадии: первая - образование активных молекул и вторая - их разложение. Если достаточная часть избыточной энергии сосредоточивается на одной связи внутри молекул, то происходит распад. В зависимости от соотношения скоростей этих стадий суммарная реакция может иметь и второй порядок.
Сначала допустим, что время между столкновениями
420
молекул велико (низкое давление) по сравнению с временем, необходимым для распада возбужденной молекулы. В этом случае большинство возбужденных молекул распадется раньше, чем произойдут новые столкновения, в результате которых возбужденные молекулы могут потерять избыточную энергию и дезактивироваться. Очевидно, в этом случае скорость реакции определяется скоростью первой стадии и должна быть пропорциональна числу столкновений, которые в свою очередь пропорциональны квадрату концентрации, т.е. будет наблюдаться второй порядок.
Если же время между столкновениями молекул мало по сравнению с временем распада (высокое давление), то скорость суммарной реакции определяется скоростью распада возбужденных молекул, т.е. пропорциональна концентрации в первой степени. Вследствие этого реакция протекает по первому порядку. Таким образом, при малых давлениях (концентрациях) реакция имеет второй порядок, а при больших - первый.
Каким путем можно установить порядок реакции? Наиболее общим методом для этого является установление зависимости концентрации от времени при постоянной температуре. Рассмотрим кинетические уравнения для реакций нулевого, первого и второго порядка.
В реакциях нулевого порядка скорость не зависит от концентраций, т.е. постоянна:
ω = -dc/dτ = k.
(XVI.2)
Зависимость концентрации от времени может быть найдена интегрированием этого уравнения: c = -kτ + B, где B - постоянная, равная концентрации в начальный момент времени. Для реакции первого порядка
ω = -dc/dτ = kc.
(XVI.3)
Чтобы найти зависимость концентрации от времени, следует проинтегрировать это уравнение, разделив переменные и взяв в качестве пределов c = c0 при τ = 0 и при τ = τ - c:
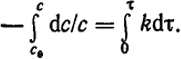
Отсюда
ln(c0/c) = kτ
(XVI.4)
или
421
k = 1/τln(c0/c).
(XVI.5)
При потенцировании уравнения (XVI.5) получаем
c = c0e-kτ.
(XVI.6)
Из уравнения (XVI.5) следует, что константа скорости реакции первого порядка имеет размерность τ-1 и, следовательно, ее численное значение не зависит от единиц, в которых выражается концентрация.
Из уравнения (XVI.6), видно, что концентрация исходного вещества экспоненциально уменьшается со временем τ, прошедшим с начала реакции. Из уравнения (XVI.4) следует, что логарифм концентрации линейно уменьшается со временем (так как lnc = lnc0 - kτ). Это показано на рис. XVI.2, а и б, где прямая и кривая линии построены в разных координатах. Если опытные данные укладываются на прямую линию в координатах ln сτ в широком интервале концентраций, то это может служить доказательством того, что рассматриваемая реакция имеет первый порядок.
Часто уравнение (XVI.4) используют в несколько другой форме: вводят концентрацию х образовавшегося к моменту τ продукта реакции, а начальную концентрацию c0 обозначают через а. В этом случае ln (a/a - x) = kτ.
Для характеристики реакций часто наряду с величиной константы скорости пользуются величиной времени полупревращения τ 1/2 т.е. времени, в течение которого претерпевает превращение половина исходного вещества c = c0/2. Очевидно, для реакций первого порядка, согласно уравнению (XVI.4), τ1/2 = (1/k)ln2 не зависит от исходной концентрации.
Для реакций второго порядка, если реагенты имеют одинаковые концентрации, кинетическое уравнение имеет вид
-dc/dτ = kc2.
(XVI.7)
После разделения переменных и интегрирования получим
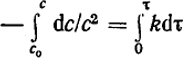 и (1/с) - (1/с0) = kτ
(XVI.8)
и (1/с) - (1/с0) = kτ
(XVI.8)
Отсюда следует, что для реакции второго порядка должна соблюдаться прямолинейная зависимость между величинами 1/с и τ.
Время полупревращения при реакциях второго порядка зависит от начальной концентрации, т.е. τ1/2 = 1/kc0
422
Пусть в реакции второго порядка принимают участие два вещества, начальные концентрации которых равны а и b, и оба вещества входят в реакцию с одинаковыми стехиометрическими коэффициентами. Если к моменту времени τ в единице объема прореагируют количества этих веществ, равные х, то скорость реакции выразится уравнением
dx/dτ = k(a - x)(b - x).
(XVI.9)
После интегрирования уравнения (XVI.9) в пределах от x = 0 при τ = 0 до х при τ = τ
 (XVI.10)
(XVI.10)
При а = b уравнение (XVI.9) упрощается, т.е.
dx/dτ = k(a - x)2.
(XVI.11)
Константа скорости реакции второго порядка имеет размерность [τ-1M-1L3] и ее численное значение зависит от единиц, в которых выражается концентрация.
Для реакции n-го порядка время полупревращения выражается формулой
τ1/2 ≈ 1/an - 1
(XVI.12)
Подобные соотношения иногда используют для определения порядка реакции.
В реальных условиях химические процессы часто не ограничиваются какой-либо одной реакцией. Например, в параллельных реакциях исходное вещество или несколько исходных веществ одновременно реагируют по различным путям и образуют различные продукты. Например, бензол и хлор могут реагировать по двум направлениям:
а) C6H6ж + Cl2г → С6H5Clж + HClг и
б) C6H6ж + 3Cl2г → С6H6Cl6ж.
В таких случаях каждая из реакций протекает независимо от других и общее изменение концентраций определяется суммированием изменений, обусловленных частными реакциями.
Большое значение для понимания сложных процессе имеет рассмотрение последовательных реакций, в которых продукты, образующиеся первыми, вновь подвергаются превращению в следующей реакции, т.е. весь процесс состоит из двух или более последовательных стадий. На промежуточных стадиях образуются неустойчивые вещества.
423
Например, при горении углеводородных топлив конечными продуктами являются СО2 и Н2О, однако в ходе реакций образуется ряд промежуточных веществ (спирты, кислоты, кетоны, различные радикалы).
Рассмотрим простейшую последовательную реакцию, состоящую из двух реакций первого порядка с константами скорости k1 и k2:
A
B
C.
Если величины k и k2 соизмеримы, то с самого начала будет проходить накопление промежуточного продукта В. Это обусловлено малыми его концентрациями в первый период процесса и, следовательно, малой скоростью распада.
Однако по мере накопления В увеличивается и скорость его исчезновения по реакции 2. В результате через некоторое время концентрация этого промежуточного продукта достигнет максимальной величины. Если же константа скорости первой реакции намного превышает константу скорости второй (k1 ≫ k2), то общая скорость превращения А в С определяется скоростью более медленной второй реакции. В этом случае количества вещества В, поставляемые реакцией 1, не успевают превратиться в С из-за медленного протекания реакции 2. Поэтому вторую реакцию называют лимитирующей или лимитирующим звеном. Очевидно, при k1 ≪ k2 лимитирующей будет первая реакция.
Вернемся к случаю, когда величины k и k2 почти не отличаются друг от друга. Пусть перед началом реакции в момент времени τ = 0 в единице объема имеется 1 моль вещества А очевидно, В и С, отсутствуют. Через время τ образуется х молей В и остается (1 - х) молей А (для простоты принимаем стехиометрические коэффициенты при А, В и С равными единице). Одновременно с образованием В происходит его превращение в конечный продукт С, количество молей которого к моменту τ равно у.
Следовательно, к моменту τ число молей вещества В в единице объема составит (x - y). Отсюда скорость образования B dx/dτ = k1(1 - x), а скорость превращения В в Cdy/dτ = k2(x - y).
Из первого уравнения, как было показано выше, следует, что
ln(1/1 - x) = k1τ или x = (1 - e-kτ).
Подставляя это значение х в выражение для dy/dτ, получим дифференциальное уравнение
424
dy/dτ = k2(1 - e-k1τ) - k2y,
имеющее следующее решение:
y = 1 + (k1/k2 - k1)e-k2τ - (k2/k2 - k1)e-k1τ.
(XVI.13)
Видно, что при τ → ∞ y → 1 , т.е. A полностью превращается в С.
Для того чтобы найти концентрацию В, следует вычесть из х число молей превратившихся в С, т.е. у
x - y = (k1/k2 - k1)(e-k1τ - e-k2τ).
При τ = 0 и τ → ∞ концентрация В равна нулю, а в ходе реакции принимает промежуточные значения. Время достижения максимальной концентрации В, определяемое из условия d(x - y)/dτ = 0, составляет
τmax =
.
Из этой формулы видно, что если k2 ≫ k1, то время достижения максимума концентрации В очень мало; и реакция через короткое время после начала принимает стационарный характер: скорость образования промежуточного вещества становится равной скорости его исчезновения. На рис. XVI.3 схематически показаны изменения концентраций исходного, промежуточного и конечного веществ в рассмотренной последовательной реакции в случае, когда k1 и k2 соизмеримы.
Выше рассматривались реакции, далекие от равновесия, т.е. при условии, что можно пренебречь скоростью обратного процесса. В общем случае необходимо учитывать скорость как прямой, так и обратной реакции. Например, для реакции второго порядка
H2г + I2г = 2HIг
скорость наблюдаемого процесса ω равна разности между скоростями прямой (ω1) и обратной (ω2) реакций:
ω = k1cH2с12 - k2c
.
(XVI.14)
По мере протекания реакции водород и иод расходуются, и накапливается HI. При этом уменьшается ω1 и увеличивается ω2 так, что скорость суммарного процесса падает и становится равной нулю при ω1 = ω2, когда достигается равновесие. Учитывая, что при этом ω = 0, из уравнения (XVI.14) получим:
k1c
c
=
k2(
с)
2
425
или
(c
)
2/
c
c
=
Kc,
где звездочками обозначены концентрации при равновесии.
Таким образом, константа равновесия Кс равна отношению констант скоростей прямой и обратной реакций при условии, что реакция протекает по одному и тому же пути. Основание для приравнивания скоростей прямого и обратного процессов при равновесии для одного и того же пути реакции дает принцип детального равновесия, который будет подробно рассмотрен в гл. XIX. Здесь мы ограничимся лишь следующей формулировкой: если установилось равновесие между двумя состояниями, то скорости прямого и обратного переходов по любому из возможных путей должны быть одинаковы.
При повышении температуры и постоянных, концентрациях реагентов, скорость химической реакции увеличивается и возрастает константа скорости. Температурная зависимость этой величины выражается уравнением, которое первоначально было найдено эмпирически Аррениусом:
d ln Kc/dT = E/RT2,1
(XVI.15)
где Е - постоянная величина, называемая энергией активации.
Уравнение (XVI.15), подобно уравнению изохоры Вант-Гоффа, для температурной зависимости константы равновесия (гл. III):
d ln Kc/dT = ΔU/RT2.
(XVI.16)
Очевидно, уравнение (XVI.15) может быть применено как для. прямого процесса с энергией активации Е1, так и для обратного с энергией активации Е2:
=
и
=
.
Вычитая из первого уравнения второе, получим:
=
.
(XVI.17)
Сопоставляя уравнения (XVI.16) и (XVI.17) и учитывая, что k1/k2 = Kc, получим:
E1 - E2 = ΔU.
(XVI.18)
Таким образом, разность между энергиями активации прямой и обратной реакций численно равна тепловому эффекту. Далее мы остановимся подробно на молекулярном
426
смысле энергии активации. В гл. XIV мы уже сталкивались с этим понятием как избытком энергии, необходимым для того, чтобы процесс осуществился. Иными словами, для течения реакции необходимо, чтобы исходные вещества преодолели определенный энергетический барьер. После этого они "спускаются" в конечное состояние, т.е. превращаются в продукты реакции.
Сказанное может быть пояснено рис. XVI.4, из которого видно, что, например, для экзотермической реакции в соответствии с уравнением (XVI.18) E2 - Е1 = -ΔU. Для нахождения величины энергии активации необходимо экспериментально найти зависимость константы скорости от температуры. Так как dT/T2 = -d(1/T), то уравнение (XVI.15) может быть представлено в виде
ln k k/d(1/T) = -E/R.
Отсюда следует, что в случае E ≠ f(T) должно выполняться соотношение
ln k = -E/RT + A,
(XVI.19)
где A - постоянная, т.е. зависимость ln k от (Т) должна быть линейной, как это представлено на рис. XVI.5.
Угловой коэффициент прямой линии на рис. XVI.5 численно равен E/R. Если энергия активации меняется с температурой, то зависимость ln k от 1/Т будет криволинейной. В этом случае энергия активации определяется по наклону касательной к кривой.
При E ≠ f(T) из уравнения (XVI.15) следует, что k = k∞e-E/RT, где k∞ - константа скорости при бесконечной температуре.
Часто предэкспоненциальный множитель k∞ обозначают через А и называют фактором частоты. Чем больше величина Е, тем сильнее зависит k от температуры. Для разных реакций, имеющих близкие значения k∞, удельные скорости при данной температуре тем больше, чем меньше энергия активации.
Заметим, что криволинейная зависимость ln k от 1/T в некоторых случаях обусловлена одновременным протеканием двух реакций с разными величинами энергий активации.
427
