§ 11. Зависимость поверхностного натяжения от состава раствора

Уравнение Гиббса позволяет вычислить зависимость поверхностного натяжения от концентрации, если известна Г = f(c), т.е. изотерма адсорбции. Мы видим, что для малых концентраций адсорбция должна подчиняться закону Генри, и уравнение (XV.28) принимает вид:

Г_с = -(c/RT)(dσ/dc)

или

dσ = ГRTdc;

σ

∫

σ0

  dσ = -Г

с

∫

0

  RTdc,

где σ₀ - значение σ при с = 0, т.е. величина поверхностного натяжения чистого растворителя. После интегрирования получим:

σ₀ - σ = Г_cRT = ГRT.

411

Введем обозначение для понижения поверхностного натяжения:

π = σ₀ - σ; π = ГRT. (XV.32)

Для того чтобы пояснить физический смысл этого уравнения, представим себе линию, отделяющую на поверхности растворителя область, на которой адсорбировано некоторое количество практически не растворимого в растворителе вещества.

Так как поверхностное натяжение из-за адсорбции будет уменьшено (σ < σ₀), то на единицу длины линии, отделяющей рассматриваемые поверхности, будет действовать сила π = σ - σ₀, стремящаяся увеличить поверхность раствора за счет поверхности растворителя. Эта сила характеризует стремление адсорбированного вещества расшириться и является аналогом давления газа (π-двумерное давление адсорбированного вещества).

Если вместо F ввести поверхность F_m, приходящуюся на один адсорбированный моль F_m, то уравнение (XV.34) будет иметь следующий вид: πF_m = RT. В рассматриваемом случае малых концентраций двумерное давление подчиняется уравнению идеального газа. Причины того, что это уравнение не зависит от характера движения адсорбированных молекул, идентичны причинам, обусловливающим выполнение уравнения Клапейрона для осмотического давления. Эти причины 'были рассмотрены в гл. V.

Уравнение (XV.34) для зависимости поверхностного натяжения от концентрации правильно лишь для малых концентраций, как и закон Генри, из которого оно выведено. Найдем зависимость поверхностного натяжения от концентрации, отвечающую уравнению адсорбции Лангмюра. Для этого в уравнение (XV.30) подставим уравнение Лангмюра:

Г = zbc/(1 + bc),

тогда

zbc1 + bc

  = -(c/RT)dσ/dc

или

σ

∫

σ0

  dσ = -zbRT

c

∫

0

 

dc

1 + bc

  dc.

Интегрируя, мы получим уравнение Шишковского:

σ = σ₀ - zRTln(1 + bc). (XV.33)

412

Опыт показал, что поверхностное натяжение разбавленных водных растворов капиллярно-активных веществ хорошо описывается уравнением (XV.35). При этом для данного гомологического ряда величина z оказалась постоянной. Так как z определяет число адсорбционных мест, то постоянство его означает, что максимальное число адсорбированных молекул не зависит от величины радикала. Это может осуществляться лишь в том случае, если активная группа адсорбируется на поверхности раствора, а радикалы образуют, по Лангмюру, над поверхностью "частокол".

Отметим, что выражения (XV.32), как и (XV.33), представляют собой уравнение состояния двумерного газа. При выводе уравнения Лангмюра учитывалась конечность размера молекул, но не принималось во внимание их взаимодействие. Поэтому уравнение (XV.35) соответствует уравнению Ван-дер-Ваальса с одной постоянной: p(V - b) = RT. Учет второй постоянной в уравнении Ван-дер-Ваальса, описывающей взаимодействие молекул, естественно, приводит к уравнению изотермы (XV.11).

Мы рассмотрели зависимость поверхностного натяжения от концентрации в рамках теории разбавленных растворов. Трактовка поверхностного натяжения концентрированных растворов должна позволить связать поверхностное натяжение раствора с поверхностным натяжением чистых компонентов. Для решения этого вопроса следует рассмотреть отличие раствора в середине фаз и на его поверхности (поверхностного раствора).

Очевидно, что поскольку имеется равновесие, то парциальные свободные энергии компонента поверхностного и объемного растворов должны быть равны. Однако поверхностный раствор растянут. Сила, действующая на 1 см длины, равна а.

Мы знаем, что дополнительное давление Δр приведет к возникновению в выражении для энергии Гиббса члена μΔр. Поэтому условие равновесия компонента запишется соответственно:

G_i = G

’

i

  - σF_i, (XV.34)

где G_i и G

’

i

  - парциальные энергии Гиббса компонента в объемном и поверхностном растворах; F_i - площадь, занимаемая молем компонента на поверхности раствора.

Для бинарного раствора G₁ = G′ - σF₁; G₂ = G₂ - σF₂. Считая F₁ = F₂ = F и исключая Fσ, получим:

G₁ - G

’

1

  = G₂ - G

’

2

  . (XV.35)

413

Пусть раствор как в объеме, так и на поверхности будет совершенным. Тогда

G₁ = G

0

1

  + RTlnx₁ (XV.36) G

’

1

  = G

0’

1

  + RTlnx

’

1

  (XV.37)

где х₁ - молярная доля компонента в объеме раствора; x

’

1

  - молярная доля компонента в поверхностном растворе.

Отсюда G

0

1

  - G

0’

1

  = σ₁F₁ так как σ₁F₁ и представляет собой поверхностное натяжение первого компонента.

Подставляя эти и аналогичные выражения для этого компонента в уравнение (XV.36), получим:

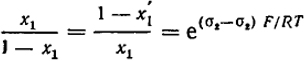(XV.38)

Введя обозначения n = 1/F для числа молей на одном квадратном сантиметре поверхности, приняв C = e^{(σ₂ - σ₂)F/RT} и решив уравнение (XV.38) относительно х

’

1

  , получим:

x

’

1

  =

x1C

1 - x1 + x1C

  . (XV.39)

Это уравнение связывает состав поверхностного раствора с составом раствора в объеме.

При адсорбции на твердых адсорбентах C = e^{A₂ - A₁/RT}, где A₁ и A₂ - адсорбционные потенциалы компонентов.

Согласно уравнению (XV.34):

σ = (G

’

1

  - G₁)/F. (XV.35)

Учитывая уравнения (XV.35) - (XV.37), получим:

σ = σ₂ - nRTln(1 - x₁ + x₁C). (XV.41)

Нетрудно убедиться, что при x₁ = 0 σ = σ₂, а при x₁ = 1 σ = σ₁. Уравнение (XV.41) является обобщением уравнения Шишковского и описывает всю область концентраций бинарного совершенного раствора. Оно было выведено А.А. Жуховицким (в 1944 г.), А. Эвансом и Э. Гуггенгеймом (в 1945 г.).

414