Уравнение БЭТ описывает адсорбцию пара на плоской поверхности. Наличие тонкой неоднородной пористости приводит к особенностям, которые описываются потенциальной теорией адсорбции Поляни и теорией капиллярной конденсации.
396
Физическая картина потенциальной теории основывается на двух свойствах сил молекулярного взаимодействия, которые будут физически обоснованы в гл. XXIII.
Эти силы аддитивны, т.е. наличие третьей молекулы не изменяет взаимодействия двух. Кроме того, эти силы не зависят от температуры. Первое свойство означает, что притяжение к адсорбенту не изменяет характера взаимодействия молекул адсорбента. Адсорбент, следовательно, лишь увеличивает концентрацию пара по сравнению с величиной ее вне поля. Это увеличение концентрации определяется величиной адсорбционного потенциала A, т.е. работой, которую надо затратить, чтобы удалить из данной точки внутри адсорбционного объема молекулу адсорбата на бесконечно далекое расстояние.
Эта величина будет зависеть от числа близких к этой точке атомов адсорбента. Поэтому потенциал внутри узких щелей будет больше по сравнению с широкими.
Согласно закону Больцмана (см. уравнение (XI.8), концентрация в точке с потенциалом А определяется уравнением
cA = c0A/RT,
(XV.16)
где с0 - концентрация вне поля адсорбента; А - потенциал, рассчитанный на 1 моль.
Таким образом, в разных точках адсорбционного поля концентрация адсорбата будет различна. Если эта концентрация достигает концентрации насыщенного пара сн, то произойдет конденсация пара. Наименьшее (критическое) значение адсорбционного потенциала, достигаемое для конденсации, определяется соответственно уравнению (XV.16) соотношением
Aкр = RT ln (cн/c0).
(XV.17)
Если температура значительно ниже критической, то плотность пара значительно меньше плотности жидкости, и при подсчете величины адсорбции можно учитывать лишь те поры, в которых A ≥ Aкр.
Объем этих пор (V) и определит адсорбционное количество Г = Vρ, где ρ - плотность жидкости. Таким образом, для определения величины Г необходимо знать распределение адсорбционного объема по величине потенциала. Однако эти сведения можно получить лишь из адсорбционного опыта. Поэтому теория адсорбции Поляни не дает абсолютных предсказаний, а связывает лишь один эксперимент с другим.
397
Рассмотрим задачу определения изотермы адсорбции при температуре Т2 по снятой для той же системы изотерме при температуре Т1. По этой изотерме надо найти указанное распределение потенциала и использовать его для предсказания изотермы при другой температуре.
Из каждой точки измеренной изотермы можно вычислить точку искомого распределения. Действительно, из величины равновесной концентрации (или давления) определяем критический потенциал по уравнению (ХУ.17), а из величины Г определим объем пор (V), занятых жидкостью.

Рис. XV.5. Характеристическая кривая адсорбции углекислого газа на угле
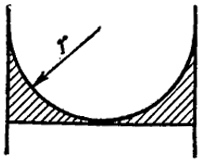
Рис. XV.6. Схема, поясняющая понижение упругости пара жидкости, имеющей вогнутый мениск
Таким образом, мы узнаем объем всех пор, потенциал которых равен или больше вычисленного значения.
Откладывая величину А в зависимости от V, получим так называемую потенциальную кривую. Типичная потенциальная кривая для активного угля и какого-либо органического вещества изображена на рис. XV.5. Точка В передает объем всех мест адсорбента.
Выше мы указали, что межмолекулярные силы не зависят от температуры. Это означает, что потенциальная кривая не зависит от температуры и может быть использована для расчета других изотерм.
Действительно, для определения величины адсорбции при некоторой концентрации c2 и температуре Т2 рассчитаем величину критического потенциала по формуле A = RT2ln(cн2/c1) , где cн2 - концентрация насыщенного пара при температуре Т2.
398
Далее, на потенциальной кривой найдем значение объема V, отвечающее координате А, а величину Г определим по формуле Г = Vρ2, где ρ2 - плотность при температуре T2.
Возможно также, как показал М.М. Дубинин, по изотерме одного вещества рассчитать изотерму другого.
На эффект действия поля адсорбента накладывается, а в некоторых случаях превалирует, эффект так называемой капиллярной конденсации. Капиллярная конденсация определяется зависимостью упругости пара от радиуса мениска. Эта важная связь описывается формулой Томсона.
Известно, что при выпуклом мениске жидкость дополнительно сжата, а при вогнутом растянута. Это дополнительное давление р описывается формулой Лапласа:
p = 2σ/r
(XV.18)
В гл. V было показано, что упругость пара (р) зависит от давления, под которым находится жидкость:
pp = p0epVm/rRT,
(XV.20)
где Vm - молярный объем жидкости.
Подставляя в уравнение (XV.19) р по уравнению (XV.18), получим формулу Томсона:
p = p0e±2σVm/rRT,
(XV.20)
где p0 - давление пара над плоской поверхностью.
Знак "минус" относится к вогнутому мениску, а "плюс" - к выпуклому.
Физический смысл уравнения Томсона станет более ясным, если его рассматривать как следствие уравнения Больцмана. Молекулы жидкости находятся, как это видно из рис. XV.6, под дополнительным притяжением заштрихованного сегмента; в случае вогнутого мениска такой сегмент по сравнению с плоской поверхностью жидкости отсутствует. Как видно из уравнения (XV.20), потенциал этого сегмента составляет 2σVm/r
Наличие капилляров со стенками, смачивающимися адсорбентом, приведет к конденсации ненасыщенного по отношению к плоскости жидкости пара. Это явление и определяет капиллярную конденсацию. При заданном значении концентрации заполняются все капилляры, радиус которых меньше заданного критического. Как и в потенциальной теории адсорбции, теория капиллярной
399
конденсации приводит к возможности предсказания одной изотермы по другой.
Согласно (уравнению (XV.20), потенциал мениска обратно пропорционален радиусу, между тем как потенциал адсорбционных сил обратно пропорционален кубу радиуса. Поэтому в тонких капиллярах преобладает эффект действия адсорбционного поля, а в широких - капиллярная конденсация.
400
