Мы сохраняли до сих пор первое положение теории Лангмюра и, следовательно, трактовали различные модели мономолекулярного слоя. Однако у большинства технических адсорбентов адсорбция не ограничивается первым слоем. С этим столкнулись при получении важной характеристики адсорбентов - их поверхности.
Уравнение Лангмюра позволяет определять поверхность адсорбента. Действительно, сравнивая опытные данные с уравнением (XV.3), можно определить число мест z. В случае молекулярной адсорбции естественно принять,
393
что величина площадки определяется величиной сечения, молекулы. Это сечение может быть определено приближенно следующим образом. Если молекулярная масса адсорбата М, а его плотность ρ, то объем моля адсорбата равен M/ρ. Объем, приходящийся на одну молекулу, составит M/NAρ, где NA - число Авогадро.
Если представить молекулу в виде куба, то величина стороны куба выразится так: (M/ρNA)1/3, а площадь сечения (M/ρNA)2/3
Таким образом, поверхность адсорбента F выразится следующим образом:
F = z(
)2/3.
(XV.11)
Однако определение поверхностей различных гелей, оксидов, катализаторов не могло быть проведено по этому методу, так как оказалось, что у этих адсорбентов изотерма обычно имеет вид, изображенный на рис. XV.4.
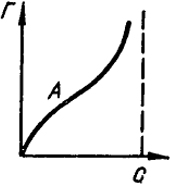
Рис. XV.4. Изотерма адсорбции БЭТ
В отличие от изотермы Лангмюра на рис. XV.4 отсутствует насыщение. Эммет предположил, что от точки Л. начинает заполняться второй слой. Это приводит к тому, что изотерма на некотором участке приближается к линейной. Тогда z может быть определена как ордината этой точки.
Однако для более точного определения поверхности возникла необходимость разработки теории полимолекулярной адсорбции. Эта теория была развита Брунаэром и Теллером. Будем считать поверхность однородной и полагать, что адсорбированные молекулы не взаимодействуют в пределах одного слоя (по горизонтали). Но и по вертикали такое взаимодействие существует, что и приводит к образованию второго и последующих слоев. На первый взгляд, учет вертикального и пренебрежение горизонтальным взаимодействием представляется противоречием. Однако на самом деле это означает лишь введение усредненной
394
теплоты адсорбции, в данном случае включающей величину взаимодействия молекул.
Примем далее, что теплота адсорбции во всех слоях (кроме первого) одинакова. Равновесие при данной концентрации и температуре уже не будет характеризоваться одним значением доли занятых мест, так как над некоторым местом будет одна молекула, над другим - две (по вертикали) и т.д. Обозначим через θi долю мест в i-том слое над поверхностью адсорбента.
Общее число адсорбированных молекул тогда определится соотношением
Г = z(θ1 + 2θ2 + 3θ3 + ...).
(XV.12)
Таким образом, для расчета Г надо знать все значения θi. Мы определим их на основе того же рассмотрения динамического равновесия, которое привело нас к изотерме Лангмюра.
Первый слой может возникать из незанятых мест в результате адсорбции или из мест с двумя молекулами в результате десорбции.
Мы рассмотрим в гл. XX принцип детального равновесия, согласно которому по каждому из путей должно установиться динамическое равновесие, заключающееся в равенстве скоростей прямого и обратного процессов для любого пути. Поэтому k1cθ0 = k2θ1.
Левая часть этого равенства, как и в выводе уравнения Лангмюра, соответствует скорости возникновения, а правая - исчезновения монослоя.
Таким же образом для второго слоя можно записать k1cθ1 = k2θ2.
Так как, согласно сформулированному предположению, второй слой не отличается от высших, то для третьего слоя k1cθ2 = k
θ
3, а для
i-того слоя
k1cθ
i-1 =
k
θ
i.
Введя обозначения k2/k1 = b; k
/
k
=
b’, получим:
θ1 = bcθ0
θ2 = b’cθ1 = bb’c2θ0
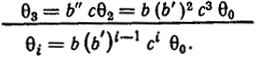 (XV.13)
(XV.13)
Число уравнений на единицу меньше числа неизвестных. Для определения θ0 можно написать еще одно уравнение из соображений нормировки: θ0 + θ1 + θ2 + ... = 1.
Подставляя соответствующие значения, получим:
θ0{1 + bc[1 + b’c + (b’)2c2 + ...]} = 1.
395
Применив формулы суммирования бесконечно убывающей геометрической прогрессии, получим:
θ0 = (1 - b’c)/(1 + bc - b’с).
(XV.14)
Подставив уравнение (XV.14) в выражения (XV.13), а затем в формулу (XV.12) получим:
Г = zbcθ0[1 + 2b’c + 3(b’)2c2 + ...].
Сумма в квадратных скобках может быть получена дифференцированием по b’c следующего равенства:
1 + b’c + (b’)2c2 + ... =
,
т.е. 1 + 2b'с + 3(b')2с2 + ... =
.
Таким образом:
Г =
| zbc |
| (1 + b’c)(1 + bc - b’c) |
.
Мы видим, что при c = 1/b’Г → ∞. Бесконечная величина адсорбированного количества вещества может быть только при конденсации. Следовательно, 1/b’ = cн, где cн - концентрация насыщенного пара.
Таким образом:
Г = zbc/(1 -
)(1 + bc -
).
(XV.15)
Эта изотерма называется по имени ее авторов - изотерма БЭТ.
Если с/сн ≪ 1, то уравнение (XV.15) переходит в уравнение Лангмюра.
Уравнение БЭТ (см. рис. XV.4) широко используется для определения поверхности адсорбента. Для этого из сравнения результатов опыта с уравнением (XV.15) определяют величину z. Затем рассчитывают поверхность по формуле (XV.11).
396
