Рассмотрим адсорбцию на однородной поверхности и будем учитывать при этом энергию взаимодействия адсорбированных молекул. Другими словами, сохраним первые два положения лангмюровской картины и откажемся от третьего. Очевидно, что в этом случае теплота адсорбции будет включать взаимодействие не только молекулы адсорбата с адсорбентом, но и адсорбированных молекул. Для определения зависимости теплоты адсорбции от заполнения рассмотрим адсорбированный слой как раствор двух компонентов - свободных и занятых адсорбционных
391
мест. Этот раствор не является совершенным, так как энергия взаимодействия соседних молекул не равна нулю, а равна нулю энергия взаимодействия вакансий. Но если эта энергия взаимодействия мала по сравнению с произведением (kT), то раствор можно считать регулярным.
Адсорбция молекулы означает увеличение числа занятых мест на единицу и уменьшение свободных мест на то же число. Поэтому вклад энергии вазимодействия в теплоту адсорбции представляет собой разницу парциальных энергий обоих компонентов раствора:
Q = Q0 + Uв - Uа,
где Uа - парциальная энергия адсорбированных молекул;
Uв - то же, вакансий; Q0 - обязано взаимодействию с адсорбентом.
В гл. XIII было показано, что
Ua = kx
;
Uв =
kx
;
Uв -
Uа =
k(
x
-
x
).
Так как xа + xв = k = 1, то Uв - Uа = k(2xа - 1).
Таким образом, теплота адсорбции должна линейно меняться по мере заполнения, т.е. Q = Q0 + βГ, где β - постоянная.
Постоянная b в уравнении (XV.6) должна зависеть от заполнения, т.е. b = b0eQ0 + βГ/RT.
Следовательно:
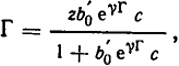 (XV.10)
(XV.10)
где b
=
b0e
Q0/RT; γ = β/
RT.
Уравнение (XV.10) было впервые выведено А.Н. Фрумкиным. Мы видим, что уравнение не решено относительно Г. Это решение представляет значительные трудности, так как уравнение трансцендентно. Мы рассмотрим наиболее интересные качественные особенности этого уравнения для случаев притяжения (β > 0) и отталкивания (β < 0)
На рис. XV.3 показано решение уравнения (XV.10) для случая значительного притяжения.
В некоторой области концентраций адсорбция убывает с уменьшением концентрации. С подобными случаями мы сталкивались при рассмотрении активности компонента
392
раствора, характеризующегося положительными отклонениями (см. гл. XIII).
Здесь, как и в области убывания адсорбции (ранее активности) с ростом концентрации, система является лабильной. Реально процесс должен осуществляться по кривой, представленной жирной линией.
Таким образом, при некоторой концентрации должен произойти скачок в адсорбции. Этот скачок, вызванный взаимодействием адсорбированных молекул, должен быть трактован как двумерная конденсация, - превращение двумерного газа в двумерную жидкость. Опыт подтвердил наличие таких скачков для ряда случаев, в частности для адсорбции паров металлов на кварце.

Рис. XV.3. Изотерма адсорбции при сильном притяжении адсорбированных молекул
Теплота адсорбции при наличии притяжения адсорбированных молекул растет, а в случае отталкивания уменьшается линейно с ростом заполнения.
Таким образом, отталкивание в этом отношении дает тот же результат, что и однородно-неоднородная поверхность. Сходство не ограничивается этим. Оказывается, что при средних заполнениях уравнение (XV.10) также переходит в логарифмическую изотерму. Таким образом, на основе изучения термического уравнения адсорбции очень трудно отделить эффект неоднородности от эффекта, вызываемого отталкиванием адсорбированных молекул.
393
