Глава XV

ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ

§ 1. Поверхностное сгущение

При рассмотрении различных систем и процессов до сих пор мы не обращали внимание на существование поверхностей раздела фаз. Так, мы полагали, что задание концентраций какого-либо-компонента во всех фазах определяет число молей этого компонента во всей системе, т.е.

378

где j - индекс фазы; L_j - число молей; x_ij - молярная доля i-того компонента в фазе.

При подсчете энергии Гиббса или любого другого интенсивного свойства системы при игнорировании границ раздела также ограничивались суммированием по фазам G = ∑G_j, где G - энергия Гиббса системы; G_j - энергия Гиббса j-той фазы.

Однако свойства фазы вблизи поверхностей раздела обличаются от свойств в середине. На поверхности может происходить специфическое поглощение компонента (адсорбция). Энергия молекул на поверхности отличается от энергии молекул в середине фаз, так как координационное число на границе меньше, чем в середине; характер движения молекул и характеристика этого движения (например, частота колебания) также будут иными на поверхности.

Возникает вопрос о целесообразных общих путях описания термодинамических свойств систем с учетом поверхностей раздела. Г. Гиббс для этой цели ввел понятие поверхностного сгущения свойств. Для учета того, что вносят в величину свойства поверхности раздела, необходимо ввести суммирование не только по объемам фаз, но и на поверхностям их разделов¹:

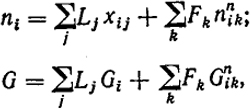
где n

π

k

  - поверхностное сгущение i-того компонента на k-той границе раздела; G

π

k

  - сгущение энергии Гиббса на этой границе.

Эти величины характеризуют вклад, который дополнительно вносит каждая поверхность раздела в величину свойств. Если увеличить какую-либо поверхность раздела при сохранении без изменения всех остальных поверхностей разделов, объемов фаз и концентрации компонентов, то число молекул в системе (или величина любого свойства) изменится. Получится поверхностное сгущение, если отнести это изменение к единице поверхности раздела. Таким образом, поверхностное сгущение энергии Гиббса G характеризует увеличение ее при увеличении поверхности

379

раздела на единицу поверхности. Если температура и давление заданы, то, как было показано в гл. II, это изменение описывает работу, которую надо совершить для осуществления процесса.

В случае однокомпонентной системы работа обратимого увеличения поверхности определяет поверхностное натяжение (σ_k). Случай растворов будет рассмотрен ниже.

Поверхностное сгущение i-того компонента на k-той границе раздела называют адсорбцией на этой границе и обозначают Г_ik:

n

n

ik

  = Г_ik.

Понятие поверхностного сгущения содержит неопределенность, связанную с выбором поверхности раздела, по обеим сторонам которой мы считаем концентрации в объемах постоянными.

Мы остановимся ниже на рациональном способе выбора такой поверхности раздела.

Наряду с адсорбцией возможно поглощение в объеме тела - "абсорбция". Оба явления объединяются словом "сорбция".

Величина Г_ik может быть положительной (если молекулы компонента притягиваются к поверхности) и отрицательной (молекулы отталкиваются от нее).

Можно рассматривать поверхностное сгущение энтропии S

π

k

  , внутренней энергии U

π

k

  и других функций.

380