Мы рассматривали лишь свойства газов и твердых тел и не обсуждали свойства жидкостей. Жидкое состояние значительно труднее поддается теоретической трактовке по сравнению с газовым и твердым. Это определяется тем, что состояния (твердое и газовое) являются предельными для всякого вещества при достаточно низких (или высоких) температурах и достаточно высоких (или низких) давлениях.
Жидкое состояние является промежуточным по своей природе. Естественно, что около критической точки жидкость близка по свойствам к газу, а при температуре, близкой к температуре плавления, - к твердому телу.
Это обстоятельство приводит к отсутствию "идеальной модели" жидкости. Для газа таковой является идеальный газ, для твердого тела - идеальный кристалл. И теории реальных газов, и теория твердых тел строятся как описание отклонений от идеальных состояний. Отсутствие идеальной модели жидкости приводит к трудности формулировки общей теории жидкости.
Такая теория должна объяснить равновесные термодинамические свойства жидкости, ее энтальпию, энтропию, уравнение состояния, температуру замерзания, поверхностное натяжение и т.п. Далее теория должна описать явления переноса - вязкость, диффузию, теплопроводность. Наконец, такая теория должна охватить явления рассеяния жидкостями различных излучений и прежде всего рентгеновского. В последние годы теория жидкостей достигла ряда серьезных успехов.
Можно указать на три основных направления развития теории жидкости. К первому принадлежат концепции развиваемые на основе какой-либо упрощенной модели жидкости. Такие модели не являются асимптотическими, т.е. строгими в какой-либо области параметров. Этим определяются сравнительно малые успехи модельных теорий, несмотря на то что попытки их построения делались на протяжении многих десятков лет.
366
Второе направление является полуэмпирическим. Его цель состоит в том, чтобы связать различные опытные характеристики жидкостей. Наконец, третье направление заключается в полном статистическом расчете, в котором используются лишь данные о энергии взаимодействия молекул. Эти данные получают либо на основе учения о строении вещества, либо из результатов измерений каких-либо свойств жидкости. Успехи третьего направления в развитии теории жидкости существенно связаны с применением электронно-вычислительных машин. Для построения моделей жидкости и выбора основных опытных характеристик жидкости целесообразно рассмотреть особенности жидкого состояния.
По величине внутренней энергии жидкость обычно значительно ближе к твердому телу, чем к газу. Теплота плавления составляет, как правило, лишь 10 % от теплоты испарения. Изменение объема при плавлении также невелико (для металлов 3 %).
Характер молекулярного движения лучше всего проявляется в величине теплоемкости. Из табл. XIV. 1 видно, что теплоемкость жидкости вблизи температур плавления близка к теплоемкости твердого тела. Следовательно, колебание молекул играет существенную роль и в жидком состоянии.
Основное (макроскопическое) отличие жидкости от твердого тела - изотропность ее свойств. Это проявляется, в частности, в том, что жидкость в отличие от твердого (кристаллического) тела не имеет определенной формы.
Таблица XIV.1. Теплоемкость Ср твердых и жидких тел вблизи температуры плавления
| Состояние вещества |
Ср, Дж/(моль·K) |
| Na |
Hg |
Pb |
Аl |
н2 |
Zn |
| Твердое |
31,8 |
28,0 |
30,06 |
28,4 |
46,8 |
30,06 |
| Жидкое |
33,6 |
28,0 |
32,2 |
26,1 |
54,6 |
33,0 |
| Состояние вещества |
Ср, Дж/(моль·K) |
| Cl2 |
Br2 |
CH4 |
HCl |
NH2 |
C0H6 |
| Твердое |
58,5 |
59,0 |
44,5 |
51,5 |
51,0 |
111,0 |
| Жидкое |
67,8 |
71,5 |
56,5 |
61,5 |
77,0 |
126,5 |
367
Микроскопической причиной анизотропности твердых тел является наличие дальнего порядка. В жидкостях имеет место лишь ближний порядок. Это приводит прежде всего к тому, что твердое тело имеет форму, определяемую кристаллической решеткой, а форма жидкого тела, как и газа, определяется формой сосуда. Жидкость обладает несравненно большей текучестью по сравнению с твердым телом. Текучесть жидкости мешает обнаружить ее упругие свойства. Если охлаждать стеклянный сосуд, полностью заполненный ртутью, то из-за большого коэффициента расширения жидкости по сравнению с твердым телом она будет упруго растягиваться, как и твердое тело.
Таким образом, и в механических свойствах нет принципиального различия между жидкостями и твердыми телами, так как первые обладают упругостью, а вторые - пластичностью. Все же очевидно, что в момент плавления происходят кардинальные изменения свойств, проявляющиеся прежде всего в исчезновении присущих кристаллическим телам постоянства формы и зависимости свойств от направления (анизотропности).
Тем не менее близость характеристик жидкости и твердого тела приводит к тому, что принимаемые для жидкости модели сохраняют некоторые черты кристаллической решетки. Мы остановимся здесь на двух наиболее распространенных моделях - "свободного объема" и "вакансий" и некоторого их развития.
Концепция свободного объема примыкает к ячеечной модели твердого тела. Будем полагать, что каждая молекула движется независимо от других в некоторой ячейке. Объем этой ячейки больше объема самой молекулы. Разница этих величин представляет собой величину свободного объема ячейки. Сумма таких объемов составляет свободный объем всей жидкости. Внутри ячейки действует некоторое поле, созданное взаимодействием молекул. В отличие от ячеечной модели твердого тела каждая молекула в жидкости движется поступательно.
Расчет термодинамических характеристик реальной системы сводится к расчету суммы состояния Z (см. гл. XIII).
Для модели свободного объема эти величины легко вычисляются, так как все сводится к расчету суммы состояния молекул:
z =
e
-ε/kTd
zd
yd
zd
pxd
pyd
pz,
368
где
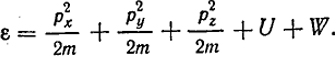
Здесь U - потенциальная энергия молекулы в центре ее ячейки, a W - энергия, зависящая от ее перемещения в ячейке.
При переходе к полярным координатам получим

Для оценки W делали различные приближения. Эту величину считали постоянной и, следовательно, равной нулю, аппроксимировали квадратичной функцией или рассчитывали как сумму парных взаимодействий с молекулами других ячеек.
В приведенной формуле остается неизвестной зависимость U к W от температуры и объема жидкости. Определив эти величины из значений одних свойств, можно рассчитать другие.
Понятие свободного объема оказывается полезным и при рассмотрении явлений переноса. Так, А.И. Бачинский принял, что текучесть (величина, обратная вязкости) должна быть пропорциональной величине свободного объема, т.е. 1/η = k(уж - Vтв), где уж и Vтв - удельные объемы жидкости и твердого тела.
Из этого уравнения следует:
η = k′(Vж - Vтв).
Это правило А.И. Бачинского хорошо согласуется с опытными данными.
Было сформулировано несколько концепций, развивающих теорию свободного объема. К ним относится предположение о флуктуации величины свободного объема в ячейках и введение разных времен пребывания молекул в состоянии колебания и в состоянии поступательного движения.
Теория вакансионной модели жидкости развита главным образом Я.И. Френкелем и Г. Эйрингом. В этой грубой полукачественной схеме игнорируется исчезновение дальнего порядка при плавлении, и жидкость рассматривается как решетка с большим количеством вакансий.
369
Как мы уже указывали, даже при температуре плавления в твердом теле молярная доля вакансий обычно меньше 0,001. Эта доля в сотни и тысячи раз больше в жидкостях.
Среднее изменение плотности металлов при плавлении составляет 3 %. Эта цифра непосредственно и будет определять долю вакансий в жидкости, если принять, что единственной причиной возрастания объема является увеличение концентрации вакансий. Резкое увеличение концентрации вакансий находится в соответствии с большой подвижностью молекул в жидкости по сравнению с твердым телом.
Большой коэффициент термического расширения жидкостей может быть отнесен к уменьшению (по сравнению с твердым телом) энергии образования вакансий и связанным с этим возрастанием их числа с ростом температуры. Скачкообразное возрастание концентрации вакансий при температуре плавления в некоторых отношениях аналогично процессу разупорядочивания. Действительно, оба процесса являются лавинными. Энергия образования вакансий зависит от числа уже имеющихся вакансий и убывает с ростом их концентрации. По аналогии с процессами скачкообразных изменений свойств (конденсации, расслоения растворов) можно полагать, что при некоторой температуре осуществляется скачок концентрации вакансий.
Эта весьма грубая концепция, выдвигающаяся Френкелем, Бреслером и Франком, игнорирует исчезновение дальнего порядка при плавлении, но содержит некоторое рациональное зерно, показывая, что уменьшение энергии образования вакансий может вызвать скачкообразный процесс.
Теория вязкости на основе модели вакансий была развита Френкелем и Эйрингом. Эта концепция аналогична приведенному во втором параграфе этой главы кинетическому рассмотрению диффузии как следствию случайных блужданий. Представим квазирешетку жидкости. Под действием силы возникает течение жидкости. Это течение с кинетической точки зрения является результатом того, что переход молекул в соседние вакансии происходит чаще в направлении действия силы, чем в противоположном. Это различие в частоте блужданий объясняется тем, что сила X, действующая на одну молекулу, уменьшает энергию активации в одном направлении и увеличивает в обратном. Эта сила производит на расстоянии пути реакции (до вершины активационного барьера) работу Xd/2, где d - период квазирешетки. Эта работа вычитается из энергии активации в направлении X и добавляется к энергии активации, отвечающей движению в противоположном направлении:
370
E+ = E - Xd/2; E- = E + Xd/2,
где Е - энергия активации блуждания в отсутствие силы X; Е+ - энергия активации блуждания в направлении действия силы; Е- - то же, в обратном направлении.
Различие в энергии активации должно привести к различию в частотах перехода в рассматриваемых направлениях (ν+ и ν-):
где ν - частота колебания молекулы.
Разница между ν+ и ν-- определяет число атомов (n), переходящих плоскость по линии центров в одну секунду:
n = ν+ - ν- = ν(e-E-Xd/2/kT)
Полагая, что работа Xd мала сравнительно с kT, получим
n = νe-E/kT(1 +
- 1 +
) =
e-
E/
kT
Для определения вязкости следует вычислить линейную скорость υ, отвечающую величине п. Так как одной молекуле отвечает сечение d2 в плоскости, перпендикулярной направлению движения, а перемещение одной молекулы означает перемещение объема, равного d3:
υ =
=
e-E/kT.
(XIV.24)
Согласно уравнению для коэффициента вязкости η, между силой X и градиентом скорости υ имеет место связь:
X = ηS(dυ/dx).
(XIV.25)
Величина S в соответствии со смыслом элементарной, действующей на один атом силы равна d2. Так как мы рассматриваем перемещение на расстояние d, то dυ/dx = υ/d.
Отсюда, учитывая уравнение (XIV.24), получим
η =
e
E/kT.
Так как d3 = Vm/NA (Vm - объем моля), то
ηVm = NA
e
E/kT.
371
Эйринг по причинам, которые будут ясны из гл. XVI, § 3, принимает XVI, §3, принимает kT/ν, где h - постоянная Планка.
Тогда
ηVm = NAheE/kT.
(XIV.26)
Формула (XIV.26), утверждающая, что предэкспоненциальный фактор обратно пропорционален молекулярному объему, является лишь грубым приближением к действительности.
Теория диффузии в жидкости в рамках модели вакансий практически совпадает с таковой для твердых тел и приводит к экспотенциальной зависимости D от 1/Т и к равенству энергий активации диффузии и вязкого течения.
Как уже отмечалось, эта зависимость для жидкости плохо выполняется, и введение понятия об энергии активации диффузии в жидкости не обосновано. В целом теория вакансий, адекватно описывающая твердое тело, позволяет лишь грубо описать отдельные свойства жидкости.
Полное описание различных свойств жидкости должно опираться на некоторые базовые функции, передающие наиболее важные ее характеристики. К таким функциям относится бинарная функция распределения, описывающая ближний порядок.
Рассмотрим жидкость, состоящую из атомов.
Поместим начало координат в ядро любого атома. Чему равняется среднее число атомов d n(r), находящихся в шаровом поясе 4πr2dr ? Эту величину можно выразить как dn (r) = 4πr2d rR(r), где R(r) - бинарная функция радиального распределения, определяющая среднее число атомов в одном кубическом сантиметре на расстоянии r от выбранного атома. Если r достаточно велико, то ближний порядок перестает действовать и R(r) не зависит от радиуса и равна среднему числу атомов в кубическом сантиметре жидкости. На расстоянии, существенно меньшем диаметра атома, функция R(r) должна быть равна нулю. Обычно она имеет максимумы на расстояниях, кратных диаметру атома, т.е. на таких, где находились бы центры атомов при соблюдении дальнего порядка. Однако величина максимума должна убывать с увеличением номера атома, т.е. из-за исчезновения ближнего порядка при увеличении расстояния от выбранного атома. В то же время ширина максимумов должна возрастать с их номером. Ситуация близка к картине случайных блужданий. Отклонение от положений, отвечающих центрам максимумов, накапливаются, и поэтому, как и в случае диффузии, ширина
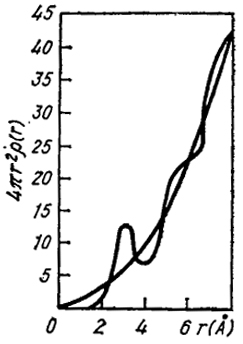
Рис. XIV.13. Атомное распределение в жидком алюминии
372
максимума пропорциональна квадратному корню из номера максимума.
Изучение рассеивания рентгеновских лучей позволяет определить величины R(r). Часто величину dn/dr, т.е. 4πr2R(r), представляют графически. На рис. (XIV.13) изображено такое распределение для жидкого алюминия. Площадь пика, соответствующая первому максимуму, отвечает среднему координационному числу в жидкости. Для тел, имеющих плотную упаковку в трердом состоянии, координационное число равно 12, а для жидкого состояния ∼11. Это означает (в рамках теории вакансий), что число вакансий составляет около 8 % (в жидкости). Между тем изменение плотности при плавлении приводит к выводу о том, что для металлов число вакансий близко к 3 %. Это противоречие иллюстрирует грубость модели вакансий.
Так называемые корреляционные функции R(n) определяют вероятность расположения п атомов в элементах объема: dV1, dV2, ..., (dWn); dWn = R(n)dV1dV2...
Парная корреляционная функция соответствует функции распределения g2 = R; корреляционная функция g3 для трех атомов может быть приближенно выражена через парные функции
g3(1, 2, 3) = g2(1, 2)g2(1, 3)g2(3, 2).
Это так называемое суперпозиционное приближение асимптотически верно для малых плотностей, но удовлетворительно выполняется для плотностей, отвечающих жидкости.
Современная теория жидкости содержит ряд уравнений, связывающих корреляционные функции с зависимостью энергии взаимодействия молекул от расстояния. Наиболее просто эта задача решается для взаимодействия твердых сфер.
Функции распределения, описывающие среднее расположение атомов, позволяют рассчитать термодинамические характеристики жидкости, если известна энергия взаимодействия двух молекул как функция расстояния ε (r).
Внутренняя энергия атомной жидкости может быть представлена уравнением
U = 3/2NkT + 2πN
r2R(
r)ε(
r)d
r.
Первый член выражает кинетическую энергию, а второй - потенциальную. Для вывода второго члена находят энергию взаимодействия любого выбранного атома с соседями
4π
r2R(
r)ε(
r)d
r, которая затем умножается на число атомов
N, деленное на два, так как мы учитывали каждую связь дважды. Если известна зависимость
R(
r) и ε(
r) от температуры, то можно рассчитать теплоемкость, энтропию, свободную энергию и составить уравнение состояния жидкости. Такого рода расчеты делают и для металлов, хотя в этом случае энергия не может быть представлена как сумма таких взаимодействий.
373
Таким образом, измерив на опыте функцию R(r), можно предсказать ряд свойств жидкости. В ряде работ функция R(r) рассчитывается теоретически. Необходимо лишь задать функцию ε(r).
Для молекулярного взаимодействия часто принимают потенциал Леннард-Джонса ε(r) = Ar-12 - Br-6. Для взаимодействия атомов - функцию Морзе
ε(r) = D(e-2α(r-r0) - 2e-α(r - r0))
и для металлов
ε(r) = [acos(βr)/r3]e-αr,
Здесь А, В, а, β, D, α, r0 - постоянные.
Мы вернемся к рассмотрению ε(r) в XXIV главе. Такие расчеты делались как для термодинамических характеристик и уравнения состояния, так и для вязкости и поверхностного натяжения. Значительно продвинулась теория жидкости благодаря применению электронно-вычислительных машин. В основном расчеты ведутся по двум методикам. В методе Монте-Карло строятся последовательности молекулярных конфигураций путем случайных смещений частиц в некоторой модельной системе.
Расчет энергии системы позволяет принимать в соответствии с уравнением (XI. 17) вес каждой конфигурации и рассчитать сумму состояний Q.
В методе молекулярной динамики решаются уравнения Ньютона с учетом сил, соответствующих энергии молекулярного парного взаимодействия при заданной соответствующей температуры энергии.
Такие расчеты проводятся для большого числа частиц (∼1000). Численные методы позволяют рассчитать корреляционные функции и термодинамические характеристики.
Определение траектории частицы в методе молекулярной динамики позволяет рассчитать характеристики переноса и, в частности, коэффициент самодиффузии.
Интересным является следующая особенность этой траектории: частицы осуществляют весьма малые "дрожательные" перемещения, в которых участвуют все соседи.
"Блуждания" являются координированными; в них участвуют сразу большое число атомов. Подобную теорию диффузии в жидкости развил Р. Свелин. Атом, согласно этой теории, совершает перемещение, когда соседи создадут в результате флуктуации необходимое для этого пространство. Поэтому теряется представление о переходном состоянии
374
и не действует экспоненциальная зависимость между D и 1//Т.
Опыт показывает, что для многих жидкостей действительно это соотношение не имеет места, хотя для других оно сохраняется.
375
