Твердое тело обычно не является равновесным. Вследствие медленного протекания процессов в нем сохраняются различные дефекты, неравновесные фазы и пр., возникающие при его производстве.
Твердые металлы состоят, как правило, из зерен. В процессе кристаллизации вокруг некоторых центров растут кристаллы. В месте встречи этих кристаллов, имеющих различную ориентацию, возникает граница зерен - некоторая область, в которой должен произойти переход от одной ориентации к другой. В зависимости от угла между направлениями ориентации кристаллов ширина границы может быть разная: от единиц до десятков и сотен межатомных расстояний.
Структура вещества на границе зерен далека от его структуры в твердом кристаллическом состоянии. На границах зерен накапливаются примеси, находившиеся в расплаве и не растворимые в твердом теле. Однако и равновесная концентрация примесей на границе может быть значительно больше, чем внутри зерен. Естественно, что растворимость в аморфной среде больше, чем в кристаллической.
Зерно не является монокристаллом; оно мозаично и состоит из небольших (10-6 - 10-4 см) кристаллических блоков. Направления кристаллизации в соседних блоках очень близки, и поэтому границы между ними значительно менее ярко выражены, чем границы между зернами.
Рассмотренные выше вакансии и атомы в междоузлиях также являются дефектами, однако равновесными. При каждой температуре имеется определенная равновесная концентрация таких дефектов, хотя мгновенная концентрация может превышать равновесную.
355
Вакансии являются одним из важнейших типов дефектов в твердом теле, определяющим протекание многих процессов и многие свойства металлов. Вблизи абсолютного нуля равновесная концентрация вакансий равна нулю, так как создание вакансии приводит к повышению энергии решетки. При высоких температурах состояние определяется минимумом свободной энергии, включающей энтропию, так как вакансии могут различным образом располагаться в решетке. Энтропия растет при увеличении числа вакансий. Для определения концентрации вакансий рассмотрим изменение энергии Гиббса, вызванное появлением в атоме твердого тела z вакансий:
ΔG = zh0 - TΔS, где
ΔS = k ln ω = k ln
.
Здесь h0 - изменение энтальпии вследствие появления одной вакансии; выражение под знаком логарифма определяет число способов размещения z вакансии в общей решетке, содержащей (z + NA) узлов.
Подставив значение ΔS в выражение для ΔG, получим
ΔD = zh0 - k T ln
,
Условие минимума ΔG может быть записано следующим образом: ΔG(z + 1) - ΔG(z) = 0, или
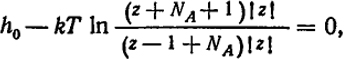
или
h0 - k T ln
= 0.
Следовательно, z/(z + NA) = e-h0/kT, где z/(z + NA) = NB - молярная доля вакансий.
Отсюда NB = e-H0/RT. H0 относится к молю вакансий. Мы считали при выводе, что вакансии вносят вклад в энтропию лишь вследствие их обмена с атомами (конфигурационная, энтропия), при этом энтропия "положения" вакансий та же, что и атома.
При вакансионном механизме для осуществления диффузионного скачка рядом с атомом должна оказаться вакансия и, кроме того, энергия атома должна превышать некоторую критическую величину Е. Вероятность такого сложного
356
события равна произведению вероятностей простых событий. Вероятность первого из них равна NB = e-h0/kT, а второго пропорциональна e-EII/kT, В результате энергия активации диффузий оказывается равной E = h0 + Eп.
Следует, иметь ввиду, что если внешние условия (например, температура) меняются быстро, стоки и источники вакансии (внешняя поверхность, границы зерен, поры, дислокаций) не успевают восстановить их равновесную концентрацию, что существенно скажется на скорости диффузии.
Особую группу дефектных кристаллов составляют так называемые нестехиометрические соединения. Например, в решетке NaCl может быть избыточный натрий. В этом случае ион избыточного натрия занимает свое место в решетке, а на месте иона Cl- оказывается электрон (F-центр). Нестехиометрические кристаллы могут быть получены за счет разницы в скоростях испарения компонентов растворов или в результате растворения одного из компонентов в соединении.
Иногда равновесные дефекты называются тепловыми, а возникшие в результате "предыстории" кристалла - биографическими. Особое значение для понимания механических свойств кристаллов, их реакционной способности и процессов кристаллизации имеет группа дефектов, объединяемая общим названием - дислокации.
В идеальном кристалле узлы образуют решетку, в которой элементарная ячейка строго повторяется со всеми своими размерами. В реальном кристалле возможны различные внутренние искривления и сдвиги, в результате которых под некоторыми узлами в месте, где должен быть другой узел, может оказаться область, соответствующая середине расстояния между узлами.
Впервые представления о дислокациях возникли в связи с необходимостью объяснить механизм пластического течения в твердых телах. В монокристалле такое течение может осуществляться в результате скольжения частей кристалла вдоль определенных атомных плоскостей. При этом нарушаются некоторые связи и должна быть затрачена известная энергия. На рис. XIV.2 показан схематически сдвиг атомной плоскости на половину атомного расстояния.
Каждый ряд есть проекция плоскости, и за каждым атомом, за плоскостью чертежа, находятся его соседи. Из первоначального состояния А система переходит в состояние В. Энергия системы U при этом повышается, так как в значительной степени разрушаются связи между атомами разных
357
плоскостей. При дальнейшем сдвиге энергия системы должна понижаться, так как атомы разных плоскостей вновь окажутся близко друг к другу. На рис. XIV.2 представлена энергия системы как функция величины сдвига. На основе теории твердого состояния можно рассчитать энергию и величину сил, необходимых для сдвига. Эти силы велики, так как все атомы нижней плоскости испытывают одинаково направленные силы со стороны атомов верхней плоскости. Расчет дает для этих сил величины на несколько порядков больше наблюдаемых. Очевидно, что в кристаллах обычно имеются какие-то дефекты, облегчающие сдвиг.
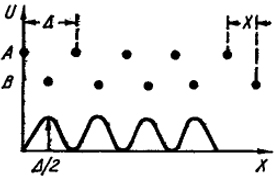
Рис. XIV.2. Схема зависимости потенциальной энергии от величины сдвига атомных плоскостей

Рис. XIV.3. Схема дефектного размещения атомов, облегчающего сдвиг плоскостей
Представим себе, что в нижней плоскости на таком же расстоянии оказывается меньше атомов (рис. XIV.3). Межатомные расстояния поэтому несколько больше нормального. Ряд атомов в нижней плоскости (считая слева) оказывается правее соответствующих верхних; какой-то атом окажется под серединой атомного расстояния, а затем атомы начнут приближаться (уже слева) к своим верхним соседям. Шесть атомов внизу размещаются на таком же расстоянии, как семь наверху. Рассматриваемый дефект резко снижает усилие, необходимое для сдвига плоскостей. Действительно, при сдвиге нижней плоскости направо только первые три атома (считая слева) будут препятствовать скольжению (они притягиваются к соседям слева), а следующие три атома будут содействовать скольжению, так как притягиваются к атомам справа.
Следовательно, если верхняя половина кристалла имеет расположение рядов атомов, отвечающее верхней строке, а нижняя - нижней, то такие половины будут легко скользить
358
относительно друг друга. Однако весьма трудно представить себе, чтобы в кристалле рассматриваемый дефект возникал сразу при переходе от одной плоскости к другой, как это было описано. Очевидно, смещение атомов, сдвиг их со своих положений равновесия должны возникать постепенно, охватывая определенную часть кристалла.
На рис. XIV.4 изображен реально существующий в твердых телах дефект - так называемая краевая дислокация. В верхнем ряду расположены семь атомов. Во втором ряду атомы начинают немного сдвигаться от краев ряда к середине, несколько уменьшая межатомные расстояния. Около середины атомы сближаются, и в четвертом ряду расстояние между сблизившимися атомами уже столь мало, что среднему атому не находится места и в ряду оказывается не 7, а 6 атомов. Если это происходит вблизи поверхности кристалла, то лишние (седьмые) атомы нижних рядов могут оказаться за поверхностью, образуя ступеньку, которая видна на рис. XIV.4.
Эта складка не является сдвигом, который изображен на рис. XIV.5. При краевой дислокации осуществлен внутренний сдвиг.
Из рис. XIV.4 видно, что часть (а не весь) кристалла внизу сдвинута вправо относительно верхней части. Линия, перпендикулярная чертежу, изображается знаком ⊥ и представляет собой границу этого сдвига. Эта же линия является дислокацией; знак ⊥ находится в центре дислокации.
Как видно из рис. XIV.4, дислокация может быть образована, если удалить из кристалла половину атомной плоскости и сомкнуть соседние плоскости вокруг образовавшегося дефекта.
Вокруг дислокаций имеют место упругие напряжения: сверху - сжатие, а снизу - растяжение. В результате перемещения атомов дислокации могут сдвинуться. На рис. XIV.6, а и б видно, что небольшие сдвиги атомов отвечают смещению дислокации вправо на одно атомное расстояние, что приводит к сдвигу одной части кристалла относительно другой.
Из рис. XIV.6, в и г следует, что тот же сдвиг в том же направлении может возникнуть, если дислокация движется в противоположном направлении. Существенно при этом, что теперь растянутой окажется область над дислокацией. Эти типы дислокаций отличают по знаку: первую считают положительной, а вторую - отрицательной. Очевидно, энергия, необходимая для создания двух дислокаций, не будет аддитивно складываться из энергий, требующихся для
359
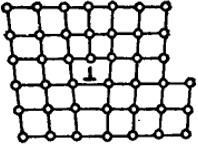
Рис. XIV.4. Краевая дислокация
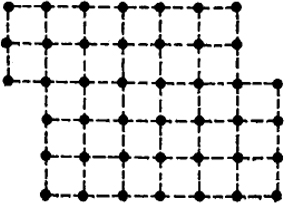
Рис. XIV.5. Схема сдвига
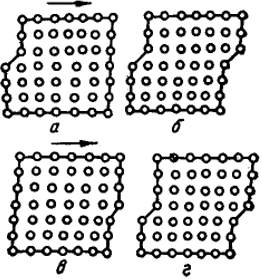
Рис. X1V.6. Деформация, возникающая при движении дислокации (стрелка показывают скалывающее напряжение)

Рис. XIV.7. Контур в идеальной решетке
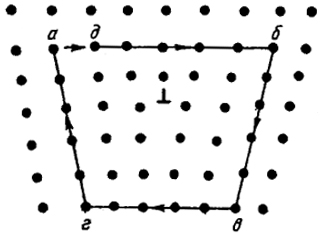
Рис. XIV.8. Вектор Бюргерса
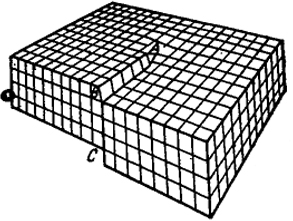
Рис. XIV.9. Винтовая дислокация
360
создания каждой из них, т.е. дислокации между собой взаимодействуют.
Дислокации одного знака взаимно отталкиваются, а разного - притягиваются, так как в последнем случае рядом с растянутой областью, отвечающей одной дислокации, окажется сжатая, отвечающая другой.
Можно показать, что сила взаимодействия обратно пропорциональна расстоянию между дислокациями. Очевидно, что как ионы в твердом теле образуют решетку, отвечающую наибольшему превышению энергии притяжения над энергией отталкивания, так и дислокации в твердом теле могут образовать решетку, в которой каждая положительная дислокация окружена отрицательными.
Вследствие взаимодействия дислокаций подвижность в такой решетке будет снижена. Это обстоятельство находится в связи с явлением наклепа при холодной обработке металлов, заключающемся в уменьшении пластичности.
Места выхода дислокаций на поверхность, как и всякие нарушения в кристаллической решетке (из-за напряжений и скоплений чужеродных атомов), легко поддаются травлению. По рисунку травления можно подсчитать число дислокаций. Оказывается, что их число на 1 см2 поверхности после деформации может достигать 1012 (в хорошо отожженном материале 108). Как показывают расчеты, энергия увеличения числа дислокаций в результате деформации близка к энергии, поглощаемой материалом при холодной обработке. Разработаны методики, позволяющие наблюдать дислокации методами электронной микроскопии.
Кроме рассмотренного типа движения дислокаций (скольжения), возможны и другие типы перемещения этого дефекта. Так, при диффузионном движении дислокации к краю экстраплоскости могут присоединяться новые атомы (например, из числа дислоцированных или ближайших соседей) или вакансии. Это будет означать, что экстраплоскость будет удлиняться или сокращаться, что приведет к переползанию дислокаций в другую плоскость скольжения. Этот тип движения дислокаций, имеющий место для линейных дислокаций, как и всякий диффузионный процесс, происходит при повышенных температурах и не связан со сдвиговыми напряжениями.
Как уже указывалось, краевая дислокация является результатом сдвига некоторой части кристалла. Поэтому дислокация может быть охарактеризована некоторым вектором, определяющим этот сдвиг,
361
Проведем в идеальной решетке некоторый контур (рис. XIV.7). Если на каждой стороне контура отсчитать одинаковое число атомов, контур замкнется. Если же попытаться провести этот контур вокруг дислокации реального кристалла, то он из-за сдвига окажется разомкнутым (рис. XIV.8).
Контур проводится в "хорошем" материале (как угодно далеко от дислокаций). Начинаем, например, от точки д н отмеряем 5 межатомных расстояний до точки б затем 5 от точки а, 5 до точки г и, наконец, 5 до точки а. Контур оказался незамкнутым. Чтобы его замкнуть, надо добавить показанный на рис. XIV.8 вектор, который носит название вектора Бюргерса. Мы видим, что вектор Бюргерса, совпадая с направлением сдвига при краевой дислокации, перпендикулярен к линии дислокации.
Другим элементарным видом дислокации является так называемая винтовая дислокация. Характер сдвига и образующиеся складки при винтовой дислокации изображены на рис. XIV.9.
Особенность, этого сдвига заключается в том, что только передняя часть правой половины кристалла по плоскости ABC сдвинута вниз. В результате получилось, что кристалл как бы состоит из одной атомной плоскости, закрученной в виде винтовой лестницы. Граница сдвига определяется перпендикуляром к поверхности кристалла в точке А, который и представляет собой винтовую дислокацию.
Для замыкания контура, проведенного вокруг этого перпендикуляра, понадобится вектор Бюргерса, параллельный направлению дислокации. Можно показать, что любая сложная дислокация может быть разложена на составляющие - краевые и винтовые.
Теория дислокации была создана в результате работ Тейлора и Френкеля в тридцатые годы, но не могла получить развития в основном потому, что не был понятен источник возникновения дислокаций. Действительно, при деформации дислокации уходят из тела, и если бы они не возникали по какому-либо механизму, то необходимое для деформации напряжение резко бы возрастало.
Такой механизм рождения новых дислокаций под действием сдвигающего напряжения носит название механизма Франка-Рида. Местами, где происходит процесс зарождения новых дислокаций (как пузырьков при кипении жидкости), являются примеси и дефекты решетки, приводящие к закреплению дислокации в двух точках. В результате под влиянием напряжения дислокация не сможет двигаться вся
362
целиком, а будет выгибаться, так как две точки ее оказываются неподвижными. Это означает, что наряду с линейными участками дислокации появятся винтовые и смешанные. В искривленной дислокации вблизи точек ее закрепления возникают участки линейных отрицательных дислокаций, у которых экстраплоскость расположена под плоскостью скольжения. Эти участки будут двигаться в обратном направлении. В результате дальнейшего движения дислокации и взаимодействия ее участков различного знака возникает замкнутая петля, охватывающая точки закрепления и внутренний отрезок между этими точками, который при выгибе способен вновь привести к повторению всего описанного цикла.
Теория дислокаций впервые позволила объяснить (помимо пластичности) такие явления, как рост кристаллов и их испарение, кинетику различных процессов в твердых телах и др. Мы вернемся к этому вопросу в гл. XVII.
Принятые в настоящее время модели границ блоков и зерен при малом угле разориентации также построены на основе теории дислокаций. Модель границы должна охарактеризовать расположение атомов, позволяющее осуществить переход от одной ориентации зерна к другой.
На рис. XIV.10 показан возможный вид границы, образованный рядами одинаковых дислокаций. Из рисунка видно, что зерна, имеющие близкую ориентацию, могут быть на границе соединены благодаря дислокациям. При этом некоторые атомные плоскости не должны проходить через весь кристалл.
Сравнение рис. XIV.5 и XIV.10 показывает, что линейные несовершенства, возникающие при этом, являются дислокациями. Как указывалось, вокруг дислокаций возникают поля упругих напряжений. Расчет энергии упругой деформации позволяет оценить зависимость энергии границ от угла поворота зерен.
Рост кристаллов из паров также не может быть объяснен без привлечения представлений о дислокациях. Этот процесс в растворах происходит путем образования двумерных зародышей (см. гл. XVIII).
Расчет для случая роста кристалла из пара показывает, что образование такого зародыша требует значительных пересыщений порядка 25-40 %. Между тем рост кристаллов из пара (например, иода) происходит при очень малом пересыщении, порядка нескольких процентов. Следовательно, этот рост происходит вследствие не образования двумерных зародышей, а адсорбции отдельных атомов на
363
плоскостях твердого тела. Такая адсорбция могла бы обеспечить рост, если бы на поверхности кристалла находились ступеньки типа изображенных на рис. XIV.4.
Теплота адсорбции благодаря большому значению координационного числа резко возрастает по сравнению с теплотой адсорбции отдельных атомов. Такие ступеньки, конечно, должны. существовать на поверхности кристалла. Однако в процессе роста при образовании плоскости все ступеньки должны зарасти и скорость роста должна резко уменьшиться. На самом деле скорость роста не уменьшается, и процесс протекает так, как будто бы на поверхности кристалла сохраняются ступеньки.
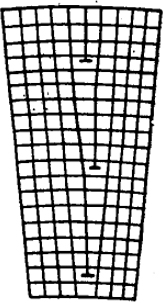
Рис. XIV.10. Схема образования границы зерна
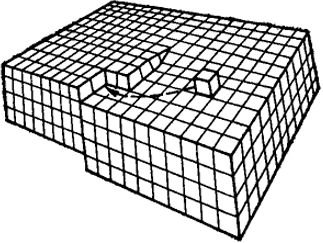
Рис. XIV.1I. Схема роста кристалла на основе винтовой дислокация
Франк объяснил это противоречие, предположив, что рост кристалла определяется винтовыми дислокациями. На рис. XIV.11 показан выход на поверхность кристалла винтовой дислокации.
Из рис. XIV.11 видно, что при адсорбции на винтовой дислокации кристалла ступеньки никогда не зарастают и должен возникнуть спиралеобразный кристалл. Микрофотографии и электронографии растущих кристаллов действительно позволяют обнаружить такие спирали.
Наличие дефектов обычно облегчает диффузию в твердом теле. Поэтому по границам блоков и в особенности зерен имеется повышенная подвижность различных атомов. Таким образом, реальный кристалл пронизан путями повышенной
364
подвижности. Энергетические барьеры на этих путях и, следовательно, энергия активации меньше, чем в объеме кристалла. Однако доля площади сечения этих путей от сечения всего кристалла очень мала.
При высокой температуре, когда величина D определяется в основном D0 и различие энергии активации играет меньшую роль, диффузия по путям повышенной проводимости не вносит существенного вклада в общий диффузионный поток, определяемый в основном объемной диффузией. При достаточно низких температурах диффузия в объеме практически не идет, и весь процессе определяется путями повышенной подвижности. Это проявляется, например, при самодиффузии серебра в том, что на прямой lgD - 1/Т (рис. XIV. 12) наблюдается перелом.

Рис. XIV.12. Температурная зависимость коэффициента самодиффузии серебра
При высоких температурах процесс характеризуется большим значением как углового коэффициента (энергии активации), так и отрезка на оси lgD (lgD0). При низких температурах обе эти величины малы.
Непосредственно пограничную диффузию можно изучать на основе применения радиоактивных изотопов. Для того чтобы судить об этих парциальных процессах по зависимости суммарной (в объеме и границах) концентрации от времени и глубины диффузии, необходимо решить, задачу о суммировании рассматриваемых потоков диффузии.
Очевидно, что они не являются независимыми. От уходящих вперед по границам "языков" диффундирующего вещества происходит отсос в объем, что затормаживает их продвижение по границам. Поэтому повышение температуры может привести к замедлению продвижения по границам, вследствие чего эффективная энергия активации может быть отрицательной.
Наряду с границами путями повышенной подвижности могут быть самостоятельные (не находящиеся на границах)
365
дислокации. Оказывается, что вдоль дислокационных трубок коэффициент диффузии может на несколько порядков превышать объемный. Случайно распределенные дислокации вносят существенный вклад в суммарный диффузионный поток лишь при достаточно низких температурах.
366
