Наибольшую трудность представляет описание диффузии в кристаллическом твердом теле. Трудно представить себе, как могут колеблющиеся атомы в условиях плотной упаковки перемещаться по решетке твердого тела.
В настоящее время предложены четыре механизма блужданий в твердом теле: 1) обмен с вакансией; 2) движение по междоузлиям;
346
3) обмен атомов 4) циклическое перемещение атомов. Первые три механизма были впервые, предложены Я.И. Френкелем, а четвертые Т.А. Лебедевым.
Согласно первому механизму, атом может совершать блуждание лишь в том случае, если по соседству с ним окажется незанятый узел, так называемая вакансия (дырка). Очевидно, что создание вакансии, т.е. перевод атома из середины на поверхность тела с оставлением свободного узла, требует затраты некоторой энергии Uв. При температуре, приближающейся к абсолютному нулю, когда энергия тела имеет минимальное значение, число вакансий должно стремиться к нулю. Однако при любой температуре Т имеется некоторая равновесная концентрация вакансий, так как равновесие определяется минимумом не внутренней, а энергии Гиббса.
Наличие вакансий приведет к увеличению энтропии, так как они могут быть распределены различным образом по решетке. Число вакансий растет с температурой и при температуре плавления может достигнуть десятых процента от общего числа узлов.
Атом, занимающий соседний с вакансией узел, может переместиться в вакансию. Такие блуждания определяют диффузию по первому из указанных механизмов. По второму механизму атом может покинуть свой узел и оказаться между узлами. Совершив некоторый путь, атом может вновь занять какой-нибудь свободный узел или вытеснить из узла атом, который начнет двигаться по междоузлиям.
Согласно третьему механизму, два соседних атома могут обмениваться местами, а согласно четвертому - некоторый цикл атомов может совершить вращение, при котором каждый атом перемещается на место соседнего.
Общим для всех механизмов являете" то, что для совершения колеблющийся атом (или несколько атомов) должен иметь некоторый избыток энергии. Действительно, при отсутствии такого избытка атом не может оторваться от своего узла, переместиться в вакансию, обменяться с соседним атомом или выйти в междоузлия.
Ранее было показано, что D = k(Δ2.τ). Если бы атом совершал перескок при каждом колебании, то время блуждания τ равнялось обратной величине частоты, т.е. τ = 1/ν. Однако атом способен совершать скачок, только если его энергия больше или равна некоторой критической величине Е. Поэтому число перескоков в единицу времени зависит от вероятности ωE иметь указанную энергию:
1/τ = νωE.
Энергия колебания описывается двумя квадратичными членами. В гл. XI было показано, что вероятность накопления двумя квадратичными членами энергии, большей Е, описывается уравнением: ωE = e-E/RT.
Таким образом, D = kΔ2/τ = kΔ2νe-E/RT
или
D = D0e-E/RT.
(XIV.19)
Параметр Е носит название энергии активации диффузии. Она определяет температурную зависимость коэффициента диффузии.
347
Величину D0 называют предэкспоненциальным фактором (множителем). Он определяет значение коэффициента диффузии при весьма высоких температурах. Так как величина перескока для ряда механизмов диффузии определяется периодом решетки d то D0 = kd2ν.
При этом мы не учитываем, что атом (или группа атомов), совершив перескок, имеет некоторую вероятность совершить вслед за этим обратный перескок. Поэтому в выражение для D0 должен входить фактор корреляции f, по величине меньший единицы. Естественно, что f зависит от механизма
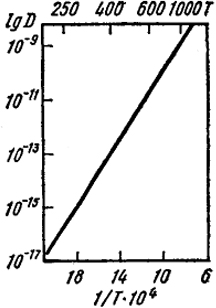
Рис. XIV.1. зависимость коэффициента диффузии золота в серебре от температуры
диффузии. Расчеты показывают, что, например, для гранецентрированной решетки при вакансионном механизме диффузии f = 0,78.
Для определения этих двух важнейших характеристик диффузии (Е и D0) необходимо измерить температурную зависимость коэффициента диффузии.
Если отложить lgD против 1/Т (рис. XIV. 1), то тангенс угла наклона прямой будет равен E/R, а отрезок, отсекаемый от Оси ординат, lgD0. Характер температурной зависимости коэффициента диффузии не может быть критерием для установления механизма диффузии, так как он одинаков для всех механизмов. Однако величины E и D0 могут быть такими критериями.
Исходя из представлений о природе металлической связи, можно рассчитать величину Е. Такие расчеты были выполнены для простейшего случая диффузии - самодиффузии. Самодиффузией называется выравнивание изотопного состава. Самодиффузия происходит, следовательно, при наличии
348
градиента концентрации какого-либо изотопа. Опыт показал, что энергия активации самодиффузии меди близка к 200 кДж/моль. Расчет для обменного механизма дал 960 кДж/моль, для механизма движения по междоузлиям с последующим обменом с атомом 1000 кДж/моль.
Наименьшее значение энергии активации при циклическом механизме отвечает кольцу, включающему четыре атома, и равно 330 кДж/моль. Только расчет для механизма вакансий дал близкий к опытному значению результат 260 кДж/моль. Таким образом, сравнение рассчитанной энергии активации с опытом показывает, что в плотноупакованных решетках (медь - гранецентрированная решетка) наиболее вероятным оказывается механизм вакансий. К аналогичным выводам приводит рассмотрение результатов расчета величины D0 (см. гл. XVI).
Вакансионный механизм диффузии в гранецентриро-ванных решетках доказывается и следующим наблюдением. Если быстро охладить сплав, можно закалить избыточную, относящуюся к более высокой температуре, концентрацию вакансий. Очевидно, избыточная концентрация вакансий должна привести к ускоренному процессу диффузии. Это действительно наблюдается, если измерять диффузию достаточно быстрыми (экспрессными) методами так, чтобы за время измерения не могла восстановиться малая, отвечающая низким температурам, равновесная концентрация вакансий. Такой эффект наблюдается, в частности, в сплаве Zn—Ag. Но наиболее важным критерием для установления механизма диффузии является изучение так называемого эффекта Киркендаля.
349
