§ 2. Диффузия

Самопроизвольное выравнивание концентрации - диффузия - вызывается блужданием диффундирующих частиц. Механизм этих блужданий может быть самым разнообразным. При диффузии газа его молекулы меняют направление своего движения при столкновении с другими молекулами.

В случае твердого тела блуждания, вызывающие диффузию, не совпадают, как в случае газа, с основным типом молекулярного движения. Колебания атомов вокруг положений равновесия не вызывают блужданий. Механизмы перемещения атомов твердого тела в соседний узел различны; они будут рассмотрены ниже. В частности, такое перемещение может произойти, если соседний узел окажется свободным.

Адсорбированная молекула может совершать блуждания по поверхности от одного адсорбционного центра к другому. Эти блуждания приводят к так называемой поверхностной диффузии. В трубке, диаметр которой меньше длины свободного пробега, молекулы газа не сталкиваются друг с другом. Блуждания возникают в результате столкновения этих молекул со стенками. При этом возникает так называемая капиллярная диффузия. Облако дыма распространяется в атмосфере из-за блужданий, вызываемых наличием в атмосфере вихрей (турбулентная диффузия).

Эйнштейн описал блуждания как движения "абсолютно пьяного человека". Пусть частица движется по линии и совершает блуждания величиной Δ за время τ. При этом знак Δ произволен. Другими словами, частица имеет одинаковую вероятность двигаться по каждому из направлений.

Если из какой-либо точки выйдет группа таких частиц, то со временем они будут расходиться, хотя среднее расстояние их от этой точки будет равно нулю, так как число частиц справа и слева будет одинаково. Величина облака этих частиц может быть охарактеризована средним квадратом расстояния х². Покажем, что эта величина пропорциональна времени. Пусть какая-либо частица после n шагов окажется на расстоянии х_п, тогда, очевидно,

x_{n + 1} = x_n ± Δ или x

2

n + 1

  = x

2

n

  + Δ² ± 2Δx_n.

341

Определим средние значения x

2

n

  и x

2

n + 1

  для многих частиц. Тогда

x

2

n + 1

  = x

2

n

  + Δ², (XIV.8)

так как среднее значение третьего члена равно нулю из-за того, что каждой его положительной величине отвечает отрицательная.

Из уравнения (XIV.8) следует, что x

2

n

  = Δ²n но n = t/τ где t - текущее время.

Таким образом, x² = (Δ²/τ)t.

Следовательно, размер "облака" частиц (√x²) растет пропорционально корню квадратичному из времени. Если в некотором объеме в начальный момент частицы будут распределены неравномерно, то со временем концентрация их будет выравниваться.

Определим поток таких частиц, вызванный неравномерностью концентрации. Сколько частиц (П) пройдет справа налево в единицу времени через площадку, имеющую поверхность S? Очевидно, что П = П→ - П←, где П→ и П← - число молекул, пересекающих площадку в направлении, указанном стрелкой.

За время τ площадку смогут пересечь лишь частицы, находящиеся от нее на расстоянии, меньшем Δ. Поэтому за τ секунд справа налево пройдут частицы, находящиеся в параллелепипеде, имеющем объем, равный SΔ. Число частиц в нем равно SΔc(x - Δ/2).

Приняв на протяжении Δ линейную зависимость с от х мы берем концентрацию в средней точке (с абсциссой x = Δ/2). Тогда П→ = [SΔc(x - Δ/2)]/2τ, так как только половина частиц движется к площадке. Соответственно П← = [SΔc(x + Δ/2)]/2τ.

П =

SΔ

2τ

  [c(x -

Δ

2

  ) - c(x +

Δ

2

  )] = -

Δ2

2τ

  S

∂c

∂x

  .

Мы видим, что поток пропорционален поверхности площадки и градиенту концентрации. Коэффициент пропорциональности носит название коэффициента диффузии D:

D = Δ²/2τ. (XIV.9)

Коэффициент 1/2 в уравнении (XIV.9) мы получили для случая движения по линии. В общем случае

D = k(Δ²/τ), (XIV.10)

342

где k зависит от геометрических условий блуждания. Природа блужданий и величина Δ могут быть самыми разнообразными. В случае газов роль блуждания играет длина свободного пробега Δ = l. Тогда

D = kl(l/τ), (XIV.11)

где l/τ - средняя скорость молекул и.

Уравнение для диффузии в газе может быть получено на основе подобного изложенному выше рассмотрения переноса свойств Ф. Мы приняли ранее, что концентрация не зависит от координат. Учет зависимости концентрации примеси с от z приводит к следующим выражениям для чисел молекул, ударяющихся снизу (ν↑) и сверху (ν↓):

ν↑ = [uSc(z - l)]/6; ν↓ = [uSc(z + l)]/6.

И, следовательно, поток компонента определяется следующим образом:

_П =

uS[c(z - l) - c(z + l)]

6

  =

uSl

3

 

dc

dz

  , (XIV.12)

откуда П = -(lu/3)(dc/dz).

Следовательно,

D = lu/3. (XIV.13)

Этот вывод сделан в предположении, что кинетические характеристики (средняя скорость, диаметр) всех молекул одинаковы. Поэтому полученное выражение для коэффициента диффузии относится к процессу самодиффузии, т.е. к выравниванию изотопного состава.

В случае выравнивания концентрации компонентов, например, бинарной смеси, различная скорость движения молекул компонентов могла бы создать на фронте диффузии градиент давления. Но возникает специфическое течение всего газа от большего давления к меньшему, приводящее к постоянству давления. Это постоянство означает, что возникает один общий коэффициент диффузии D₁₂, описывающий перенос как первого, так и второго компонента. Простейшая теория Майера приводит к следующему выражению:

D₁₂ = 1/3(x₁u₁l₁ + x₂u₂l₂),

где u₁ и u₂ - средние скорости движения молекул компонентов; l₁ и l₂ - длины путей их свободного пробега; x₂ и x₁ - молярные доли.

343

Сравнивая уравнения (XIV.13), (XIV.3) и (XIV.5), получим связь коэффициента диффузии с коэффициентом вязкости и теплопроводности:

η = Dρ; λ = DC_V0, (XIV.14)

где C_V0,- теплоемкость единицы объема.

Из формулы (XIV.9) непосредственно видно, что коэффициент диффузии измеряется в см²/с. Коэффициент диффузии газов при нормальном давлении имеет порядок 10^-1, в жидкостях 10^-5, в твердых телах 10^-10 см²/с.

Мы рассмотрели, связь коэффициента диффузии с характеристикой, зависящей от механизма процесса (с величиной блужданий). Интересно рассмотреть связь коэффициентов диффузии с понятием "подвижности", которое мы ввели при рассмотрении электропроводности. Подвижность - это скорость, которую приобретает частица при действии единичной силы. Если в двух точках раствора концентрация различна, то и величина парциальной молярной энергии Гиббса компонента G_m в этих точках будет разной. Следовательно, при переходе молекулы из одной точки в другую будет производиться работа, равная убыли энергии Гиббса: W = -G_m, где индекс т указывает на то, что энергия Гиббса относится не к молю, а к молекуле. Но работа равна произведению силы на путь. Следовательно, на молекулу в среднем действует сила f_i описываемая уравнением: f_iΔx = -ΔG_mi

или f_i = -dG_mi/dx.

Под влиянием этой силы молекулы должны получить в среднем направленное движение со скоростью υ, определяемой уравнением: υ_i = U_if_i, где U_i - подвижность.

Вычислим поток частиц через площадку с поверхностью S. В единицу времени площадку пересекут Sc_iυ_i молекул. Следовательно:

П = Sc_iυ_i = Sc_iU_i(dG_mi/dx).

Согласно формуле (V.14): G_mi = ψ

0

mi

  + kTlnc_i

Вместо R формулы (V.14) в последнем уравнении фигурирует k, так как энергия Гиббса относится к молекуле, а не к молю: ∂G_mi/∂x = (kT/c_i)(∂c_i/∂x).

Таким образом: П = ukTS(∂с/∂х).

Следовательно:

D = -UkT. (XIV.15)

344

Для подвижности U макроскопических шарообразных тел, размер которых существенно больше размера молекулы среды, согласно формуле Стокса: U = 1/6πηr, где η - вязкость среды; r - радиус шара.

Таким образом, приближенно D = kT/6πηr.

Эта формула применялась, в частности, для оценки величины коэффициента диффузии в шлаках. Из нее непосредственно следует, что диффузия в шлаках проходит значительно медленнее, так как вязкость шлаков значительно больше вязкости металлов. Поэтому в металлургических агрегатах скорость процессов обычно определяется диффузией в шлаке.

Рассмотрим диффузию бинарного электролита. Подвижность ионов различна. Однако более подвижный ион, как это указывалось в гл. IX, не может диффундировать быстрее медленного, так как при этом была бы нарушена электронейтральность. Подвижный ион, уходя вперед, ускоряет движение менее подвижного, замедляя собственное движение. Возникает обсужденный в гл. IX диффузионный двойной слой, в котором осуществлен диффузионный скачок потенциала. Помимо рассмотренной выше силы f на ионы действует некоторая сила φ тормозящая быстрые ионы и ускоряющая медленные. Поэтому скорость υ₊ и υ_- ионов обоих знаков определяются следующими уравнениями:

υ₊ = U₊(f - φ); υ_- = U_-(f - φ). (XIV.16)

Мы приняли для конкретности, что положительный ион имеет большую подвижность, т.е. что U₊ > U_-.

Из равенства скоростей следует, что U₊ > U_-, откуда

φ = f[(U₊ - U_-)/(U₊ + U_-)]. (XIV.17)

Исключив φ из уравнений (XIV.17) и (XIV.16), получим

υ₊ = υ_- = υ = [(2U_-U⁺)/(U₊ + U_-)]f.

Таким образом, вместо подвижности U в формуле для коэффициента диффузии (XIV.15) оказывается U = (2U_-U₊)/(U₊ + U) и тогда D = kT[(2U_-U₊)/(U₊ + U_-)]. Следовательно, 1/U = 1/2(1/U₊ + 1/U_-).

Другими словами, сопротивление (величина, обратная подвижности) оказывается для электролита средним арифметическим сопротивления ионов.

Представления, связанные с понятием подвижности, особенно при использовании вязкости, наиболее пригодны для

345

описания диффузии в жидкостях. Мы показали, выше, что рассмотрение диффузии как по концепции блужданий, так и по концепции подвижности приводит к одинаковому выражению для величины диффузионного потока П = -DS × (∂с/∂х).

Это уравнение называют первым законом Фика. Вторым законом Фика называют дифференциальное уравнение, описывающее изменение концентраций в пространстве и во времени. Это уравнение непосредственно следует из выражения для потока.

Рассмотрим для простоты случай, когда концентрация зависит лишь от х.

Вычислим потоки через две плоскости, находящиеся на расстоянии Δx. Через левую плоскость поток равен -DS × (∂с.∂x), а через правую -DS(∂с/∂x)_{x + Δx}. В результате за время Δt в объеме SΔх останется количество вещества

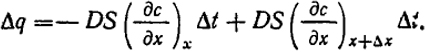
Учитывая, что

получим Δq = DS(∂²c/∂x²)SΔxΔt

Это количество приведет к увеличению концентрации со временем. Следовательно, Δq = (∂c/∂x)ΔxΔt.

Таким образом, рассмотрение баланса приводит к уравнению

D = (∂²c/∂x²) = ∂c/∂t.

Если концентрация зависит от всех трех координат, то уравнение диффузии принимает вид:

D[

∂2c

∂x2

  +

∂2c

∂y2

  +

∂2c

∂z2

  ] =

∂c

∂t

 

или сокращенно

DΔc = ∂c/∂t. (XIV.18)

346