При рассмотрении термодинамической теории растворов была дана статистическая трактовка совершенных растворов. Было показано, что при образовании совершенных растворов изменение энтальпии ΔH = 0, а изменение энтропии определяется формулой (V.28).
Как указывалось, отклонения от законов идеальных растворов могут быть классифицированы по невыполнению этих двух соотношений.
Для регулярных растворов отклонение определяется лишь наличием теплоты смешения, так как изменение энтропии при их образовании такое же, как при образовании
319
совершенных растворов, и описывается формулой (V.28).
Целесообразно рассмотреть отклонения парциальных энтальпий и энтропии компонентов реального раствора от тех же величин компонентов совершенного раствора.
Из отношения ΔH = 0 следует, что Hi = H
, а из уравнения (V.28)
Si = S
- Rlnxi,
(ХIII.35)
где H
и
Si - соответствующие характеристики чистых компонентов;
Hi и
Si - парциальные характеристики компонентов совершенного раствора.
Согласно уравнению (VI.1) μi = μ
+
RTln
ai, а по уравнению (V.29) μ
i,сов.р. = μ
+
RTln
xi
Вычитая второе уравнение из первого, получим после простых преобразований
ai = xie(μi - μi,сов.р.)/RT
или
ai = xie(Hi - H
)/RTe -(Si - Si,сов.р.)/R.
(XIII.36)
В регулярных растворах третий множитель равен единице и отклонения от совершенных растворов определяются вторым множителем.
Теория регулярных растворов была впервые дана Гильдебрандом.
Рассмотрим простейший вариант этой теории в рамках так называемой "модели решетки". Будем учитывать лишь взаимодействие соседей и полагать, что координационное число z (число соседей) одинаково у обоих чистых компонентов и в растворе.
Пусть энергии взаимодействия атомов (или молекул) компонентов равны (см. гл. V) соответственно ε1-1, ε1-2 и ε2-2. Индексы внизу обозначают сорт взаимодействующих молекул, например, ε2-2 обозначает энергию взаимодействия двух молекул второго компонента.
Средняя кинетическая энергия атомов компонентов, согласно закону распределения по степеням свободы, не зависит от состава и при образовании раствора не происходит изменения кинетической энергии Uк. Поэтому при расчете ΔH раствора можно ограничиться лишь величиной потенциальной энергии Uк. Будем считать объем раствора аддитивным. Поэтому
ΔH = ΔUп + ΔUк + pΔV = ΔUп.
320
Определим потенциальные энергии компонентов U
и
U
. Число молекул в моле равно числу Авогадро (
NA). Поскольку в каждой связи участвуют две молекулы, то общее число связей в одном моле компонента будет
NAz/2 и
U
=
, U
=
.
(XIII.37)
В растворе, состоящем из L1 атомов первого компонента и L2 атомов второго компонента, представлены связи трех типов: 1-1, 1-2 и 2-2.
Обозначим число этих связей соответственно p1-1, p1-2 и p2-2 Тогда
Uп = p1-1ε1-1 + p2-2ε2-2 + p1-2ε1-2.
(XIII.38)
Расчет потенциальной энергии сводится к определению трех величин: p1-1, p1-2 и p2-2.
Два уравнения для определения этих величин можно получить из нормировки. Действительно, каждый атом протягивает z "рук", образующих связи. Таким образом, в растворе представлено L1z "рук" первого сорта. Эти "руки" использованы для образования р1-1 связей сорта 1-1, требующих каждая двух таких "рук", и p1-2 связей 1-2, требующих одной "руки" каждая.
Следовательно:
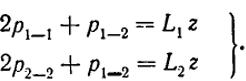 (XIII.39)
(XIII.39)
Мы видим, что из трех неизвестных величин две определяются этими уравнениями, а независимой остается только одна. В качестве такой удобно выбрать р1-2. Из уравнения (XIII.39) получим
p1-1 = (L1z - p1-2)/2 и p2-2 = (L2z - p1-2)/2.
(XIII.40)
Подставив уравнение (XIII.40) в (XIII.38), получим

Учитывая выражение (XIII.37) и введя обозначение
Δ = 2ε1-2 - ε1-1 - ε2-2,
получим
ΔUп = p1-2Δ/2.
(XIII.41)
321
В случае регулярных растворов, несмотря на то, что раствор образуется с поглощением или выделением тепла, изменение энтропии такое же, как у совершенных растворов. Это означает, что число перестановок атомов таксе же, как у совершенных растворов. При расчете энтропии совершенного раствора мы учитывали все перестановки. Следовательно, и у регулярного раствора отсутствует ассоциация молекул и осуществляются все перестановки.
Таким образом, несмотря на наличие энергии взаимодействия, в регулярном растворе не образуется никакого порядка, и поэтому величина р1-2 определяется вероятностью встречи двух разнородных атомов.
Общее число связей в растворе составляет (L1 + L2)z/2.
Вероятность встречи двух разнородных атомов определяется как вероятность сложного события. Вероятность того, что первый атом связи будет атомом первого компонента, равна L1/(L1 + L2).
Вероятность того, что второй атом связи будет атомом второго компонента, соответственно равна L2/(L1 + L2).
Вероятность одновременного осуществления этих событий равна L1L2/(L1 + L2)2.
Если атомы поменяются местами, все равно будет осуществлена связь 1-2.
Таким образом
p1-2 =
=
(XIII.42)
и
ΔUп =
.
Теплота образования раствора, рассчитанная на один моль,
Qp = -ΔH/(n1 + n2); n1 = L1/NA; n2 = L2/NA,
где n1, n2 - числа молей обоих компонентов в растворе.
Таким образом, так как ΔH = ΔUп
Qp =
= -
x1x2,
(XIII.43)
где х1 и х2 - молярные доли компонентов.
Мы видим, что раствор будет совершенным, когда Δ = 2ε1-2 - ε1-1 - ε2-2 = 0, т.е. если ε1-2 = (ε1-1 + ε2-2)/2.
Следовательно, для этого не требуется равенство всех энергий взаимодействия. Достаточно, чтобы энергия взаимодействия
322
разных атомов была средним арифметическим энергий взаимодействия одинаковых атомов. В этом случав энергия образования разнородных связей из однородных равна нулю. Этот процесс может быть описан следующим уравнением:
(1 - 1) + (2 - 2) = 2(1 - 2)
(XIII.44)
Скобки означают связи. Изменение энергии при осуществлении этого процесса равно Д. Характер отклонения от закона Рауля и знак теплового эффекта определяются по уравнению (XIII.43) знаком Δ.
Поскольку за нуль потенциальной энергии принимают энергию разделенных молекул, то все величины е отрицательны. Если притяжение разных атомов больше, чем полусумма притяжений одинаковых (Δ < 0), то при образовании раствора выделяется теплота, что приводит к отрицательным отклонениям от закона Рауля.
Уравнение (XIII.43) передает зависимость теплоты образования раствора от состава. Эта зависимость выражается симметричной кривой, имеющей максимум при x1 = x2 = 0,5.
Уравнение (XIII.43) может быть переписано следующим образом: Q = 4Qmx1x2, где Qm - максимальная теплота образования регулярного раствора.
Согласно уравнению (XIII.43), энтальпия регулярного раствора может быть выражена следующим уравнением:

Отсюда
H1 =
=
H
+
или
H1 - H
=
x
.
Учитывая уравнение (XIII.36), получим:
a1 = x1eνx
;
(XIII.45)
a2 = x2eνx
где γ = zNAΔ/2RT.
Если Δ < 0, γ < 0б то a1 < x1, т.е. имеют место отрицательные отклонения от закона Рауля. Положительные отклонения могут привести к ограниченной растворимости.
323
При больших значениях γа1, как функция х1, будет характеризоваться двумя экстремумами (рис. XIII.1).
Наличие трех концентраций с одинаковой активностью означает существование трех равновесных растворов. Однако средняя концентрация отвечает неустойчивому раствору, у которого активность падает с ростом концентрации.
С повышением температуры максимум и минимум сближаются; при критической температуре смещения они совпадают и при критической концентрации дают точку перегиба.
Определим параметры критической точки. В точке перегиба ∂a1/∂x1 = 0. Следовательно:
∂a1/∂x1 = eγx
2γx2 = 0.
Отсюда 2γx1x2 = 1.
Учитывая, что Xi = l-x1, получим
x1 = (1/2) ± √1/4 - 1/2γ.
(XIII.46)
Два экстремума сольются вместе, если γ = 2, т.е. zNAΔ/2RTкр = 2.
Следовательно:
Tкр = zNAΔ/4R = -1Qm/R.
Из уравнения (XIII.46) следует, что (x1)кр = 1/2
Кривая, описывающая зависимости растворимости от температуры для растворов близких к регулярным, должна быть близка к симметричной, другими словами, растворимости в α- и β-фазах должны быть приблизительно равны.
Малая растворимость по теории регулярных растворов является следствием малой величины ε1-2 по сравнению c ε1-1 и ε2-2. Это может осуществляться потому, что молекулы одного из компонентов обладают значительным дипольным моментом, что приводит к большей величине электростатического взаимодействия (ε1-1). Если даже молекулы второго компонента не обладают дипольным моментом, то их взаимодействие друг с другом (ε2-2) может быть все же велико, если велика поляризуемость α.
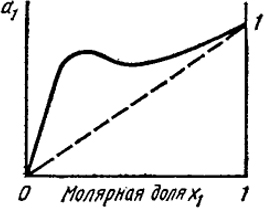
XIII.1. Активность компонента раствора в случае ограниченной растворимости
324
Однако дипольная и недипольная молекулы слабо взаимодействуют друг с другом, т.е. ε1-2 мало. Поэтому обычная растворимость дипольных веществ в недипольных (например, воды в бензоле) мала. По тем же причинам мала растворимость недипольных веществ в дипольных.
Взаимная растворимость твердых компонентов будет рассмотрена в гл. XXII. Все выведенные выше количественные соотношения верны, естественно, лишь в рамках сделанных приближений.
Рассмотрим кратко наиболее типичные отклонения. Прежде всего основное положение теории регулярных растворов (ΔS = ΔSсов), как указывал Э. Гуггенгейм, противоречит условию Δ = 0. Действительно, если энергия реакции (XIII.44) не равна нулю, то число p1-2 определяется не только вероятностью встреч атомов, но и величиной Δ.
Другими словами, равновесие, выраженное уравнением (XIII.44), сдвинуто в левую или правую сторону. Описание этого равновесия должно дать третье уравнение для определения трех величин p1-1, p1-2, p2-2. Это равновесие может быть описано следующим образом:
x
x1-1x2-2 = K,
(XIII.47)
где x1-2, x1-1 и x2-2 выражают молярные доли соответствующих связей от общего числа связей. Другими словами
x1-2 = p1-2/p; x1-1 = p1-1/p; x2-2 = p2-2/p,
где p = p1-2 + p2-2 + p1-2; K - константа равновесия.
Исключив p1-1 и р2-2 из уравнений (XIII.47) и (XIII.40), получим
| 4p1-2 |
| (zL1 - p1-2)(zL2 - p1-2) |
= K.
(XIII.48)
Это уравнение позволяет определить величину p1-2. Приняв, что порядок отсутствует, мы ранее получим для регулярных растворов
p1-2 = zL1L2/(L1 + L2).
Подставив это выражение в уравнение (XIII.48), получим K = 4. Если степень порядка невелика (например, при высокой температуре), то K близко к 4, а р1-2K (zL1L2)/(L1 + L2).
Пусть
K = 4(1 + δ), а p1-2 =
(1 + α).
где δ и α - малые величины.
325
Введя эти значения в уравнение (XIII.48) и пренебрегая малыми величинами второго порядка, получим α = δx1x2.
Таким образом,
p1-2 =
(1 + δ
x1x2).
Зависимость K от температуры выразится уравнением
K = K0 = K0eQ0/kT
где K0 = 4, так как при T → K = K0 = 4.
По уравнению (XIII.44) Q = -NAΔ.
Таким образом,
K = 4e-Δ/kT.
Для высоких температур (kT ≫ Δ) K = 4 [1 - (Δ/kT)], следовательно, δ = -Δ/kT, и
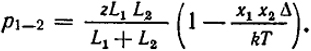 (XIII.49)
(XIII.49)
Уравнение (XIII.49) учитывает наличие некоторого порядка в расположении связей. Таким образом, допущение беспорядочного расположения атомов, являющееся основным в теории регулярных растворов, правильно для достаточно высоких температур.
Интересно проанализировать, как возникновение порядка скажется на теплосодержании и энтропии раствора.
Из уравнений (XIII.41) и (XIII.49) следует, что
ΔH = ΔU =
zΔ -
.
Таким образом, энергия упорядочения ΔUуп, обязанная наличию порядка, определится следующим соотношением:
ΔHуп = ΔUуп = -
(XIII.50)
Мы видим, что при любом знаке Δ энергия взаимодействия всегда понижается из-за наличия порядка, который собственно поэтому и возникает.
Очевидно, что энтропия должна уменьшиться из-за возникновения порядка, который уменьшает число конфигураций.
Величины ΔGуп и ΔSуп можно определить, пользуясь термодинамическим соотношением
ΔGуп = -T∫
d
T +
JT.
326
Согласно уравнению (XIII.50), ΔHуп = a/T, где а не зависит от T. Отсюда
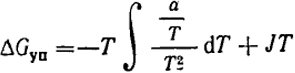
или
ΔGуп = (a/2T) + JT.
Так как при T → ∞ ΔGуп = 0, то J = 0. Таким образом:
ΔGуп = ΔHуп/2.
(XIII.51)
Учитывая, что ΔGуп = ΔHуп - TΔSуп, получим TΔSуп = ΔHуп/2.
Таким образом, половина выигрыша энергии при процессе упорядочения теряется из-за уменьшения энтропии.
Уравнение (XIII.51) обосновывает теорию регулярных растворов как приближение для высоких температур. Действительно, ΔGуп обратно пропорционально температуре как и ΔHуп. Следовательно, при достаточно высоких температурах можно пренебречь влиянием упорядочения на ΔH и ΔS.
При рассмотрении энтропии раствора следует учесть, что в энтропии растворов наряду с членом, описывающим перестановки атомов (конфигурационная энтропия), следует рассматривать член, связанный с колебаниями атома около положения равновесия (позиционная энтропия). Дело в том, что, как видно из формул (XIII.2) и (XIII.3), энтропия убывает с частотой колебания, а эта величина меняется с составом.
Для сплавов, как указано, существенно новым обстоятельством является влияние на энергию раствора электронов проводимости. Эти вопросы будут рассмотрены в гл. XXIII в связи с теорией металлического состояния.
До сих пор принималось, что все места в решетке раствора эвивалентны. В твердых растворах возможны, однако, случаи, когда имеются места разного типа. При этом возможно, что атомы одного из компонентов предпочтительно или целиком выбирают определенные места. Наиболее простым случаем этого типа является раствор внедрения. Известно, например, что аустенит представляет собой решетку внедрения. В решетке γ-железа (гранецентрированная кубическая решетка) между атомами железа имеются поры (междоузлия), в которые могут поместиться малые атомы углерода. Из-за большого различия в радиусах атомы
327
углерода и железа не могут дать раствора замещения.
Определим термодинамические свойства раствора внедрения. Пусть на каждый атом растворителя приходится r мест для внедрения атомов. Тогда для L2 атомов растворенного вещества L1r атомов растворителя представляют L1r мест.
Число способов, каким L2 атомов распределяются по L1r местам:

Отсюда изменение энтропии при образовании раствора
ΔS = kln
.
Используя формулу Стирлинга, получим
ΔS = k{L1r;lnL1r - L2lnL2 - (L1r - L2)ln(L1r - L2)}
и энтропия раствора
S = nS
+
nS2 + Δ
S, где
S2 - постоянная величина;
n2 =
L2/
NA;
S2 =
=
S2 +
Rln
=
S2 +
Rln
.
Если принять, что теплота растворения не зависит от концентрации, то парциальное теплосодержание Н2 не должно зависеть от состава. Поэтому
G2 = H2 - TS2 = G′ - RTln(x1r - x2)/x2,
где G′ = H2 - TS2 не зависит от состава.
Так как G2 = Gст + RTlna2, то активность определяется соотношением a2 = x2/(x1r - x2). Активность, определенная таким способом, дает для разбавленных растворов a2 = x2/r, что не соответствует обычному выбору стандартного состояния.
Для того, чтобы в разбавленных растворах a2 = x2, целесообразно принять a2 = x2r/rx1 - x2.
Это отвечает следующему выбору стандартного состояния:
G
=
G′ +
RTln
r
М.И. Темкин и Л.А. Шварцман, которым принадлежит это рассмотрение растворов внедрения, показали, что хорошее совпадение с опытом может быть получено для активности углерода в аустените, если принять r = 1/4.
328
На самом деле, как показывает рассмотрение гранецентрированной кубической решетки, r = 1. Поэтому вышеприведенные формулы должны рассматриваться как полуэмпирические.
Разные типы мест для атомов могут быть реализованы и в случае раствора замещения. Так, например, латунь (β) имеет объемноцентрированную кубическую решетку. Оказывается, что энергия решетки будет иметь меньшее значение, если атомы меди расположатся в центрах, а атомы цинка - в вершинах куба. При низких температурах действительно осуществляется порядок этого типа, а при высоких - неупорядоченное состояние. При каждой температуре можно определить число атомов, находящихся на "своих" (L1) и "чужих" (L2) местах.
Очевидно, что при очень высоких температурах (полный беспорядок) L1 = L2 = L/2, а при низких L1 = L и L2 = 0 (L - общее число атомов).
В качестве параметра, характеризующего степень упорядоченности, естественно принять γ = [(L1 - L2)/(L1 + L2)]2.
Всегда положительный по знаку коэффициент γ меняется от 1 (полный порядок) до 0 (полный беспорядок).
Мы не будем излагать статистических теорий зависимости степени упорядоченности от температуры, а рассмотрим наиболее важный результат - наличие точки Кюри. Естественно, что Y уменьшается по мере повышения температуры от своего наибольшего значения (γ = l). Однако наименьшее значение (γ = 0) достигается не асимптотически, по мере повышения температуры, а скачком при некоторой температуре.
Таким образом, существует некоторая характеристическая температура (точка Кюри), выше которой имеется полный беспорядок, а ниже - усиливающийся при дальнейшем понижении температуры порядок. Такое превращение носит название фазового перехода второго рода. В отличие от фазовых переходов первого рода при фазовых переходах второго рода термодинамические функции не изменяются: ΔV = 0; ΔH = 0; ΔS = 0; ΔG = 0; ΔE = 0.
В точке Кюри порядка еще нет, он только возникает с понижением температуры, и свойства фазы (энергия, энтропия, объем и пр.) не меняются скачком. Поэтому фазовые переходы второго рода не сопровождаются тепловым эффектом. Однако по некоторым свойствам упорядоченная фаза должна отличаться от неупорядоченной.
Рассмотрим, например, теплоемкость. При повышении температуры неупорядоченной фазы энергия должна быть
329
затрачена лишь на изменение энергии колебания решетки, а для упорядоченной фазы с повышением температуры должна уменьшаться упорядоченность, что потребует дополнительной затраты энергии.
Таким образом, теплоемкость упорядоченной фазы больше теплоемкости неупорядоченной, и в точке Кюри теплоемкость скачкообразно изменяется. Упорядоченность исчезает с повышением температуры скачком, потому что этот процесс носит лавинный характер. По мере уменьшения упорядоченности выигрыш от расположения атомов в своих местах по сравнению с чужими уменьшается. Это обстоятельство усилит неупорядоченность, которая по мере повышения температуры будет нарастать, и порядок полностью исчезнет в точке Кюри.
330
