§ 7. Энергия электронного газа

Каждый электрон металла движется в поле, создаваемом всеми ядрами и остальными электронами металла. В грубом приближении можно принять, что ядра и остальные электроны образуют в объеме металла некоторое постоянное, не зависящее от координат, поле. Электроны, однако, не могут не иметь кинетической энергии в этом поле даже при абсолютном нуле.

317

Состояние, при котором они все имели бы скорость, равную нулю, противоречило бы принципу Паули.

Определим кинетическую энергию электронного газа при абсолютном нуле. При этом электроны заполняют области фазового пространства от импульса, равного нулю, до некоторого наибольшего значения р_т

Общий объем фазового пространства, занимаемый электронами, должен равняться Nh³/2, так как в каждой ячейке объемом h³ помещаются два электрона с насыщенными спинами, а число электронов равно N.

Таким образом, 4πp

3

m

  V/3 = Nh³/2

и

p_m = ³√(3h³/8π)n, (XIII.29)

где n = N/V(V - объем, в котором находятся электроны). Число электронов, имеющих импульс в интервале между р и p + dp, составит

4πp²Vdp/(h³/2).

Таким образом, кинетическая энергия электронного газа при абсолютном нуле будет

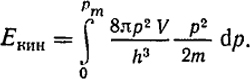
Величина Е_кин, носящая название нулевой энергии электронного газа, растет с плотностью газа. Интересно сравнить среднюю энергию E_кин/N с максимальной энергией. Согласно уравнению (XIII.29):

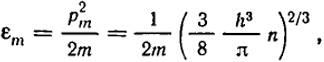
а согласно уравнению (ХIII.30)

(XIII.31)

отсюда

ε = 3/5ε_m. (XIII.32)

Нулевые энергии электронов в металлах очень велики. Если подставить в уравнение (XIII.31) значение числа электронов в единице объема (n) для серебра, то окажется, что для одного моля электронов E_кин = 288000 Дж/моль:

Найдем температуру, при которой, согласно закону распределения

318

по степеням свободы, газ мог бы иметь такую энергию: 288000 = 3RT/2 и T = 23000 К.

Несмотря на большую энергию электронного газа, теплоемкость его равна нулю, так как вследствие вырождения эта энергия не зависит от температуры. По мере повышения температуры вырождение будет сниматься и энергия электронного газа начнет медленно увеличиваться с повышением температуры.

Расчет показывает, что при низких температурах энергия электронного газа может быть описана следующей формулой:

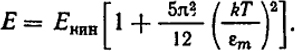(XII.33)

Здесь E_кин выражается формулой (XIII.30) для энергии электронного газа при абсолютном нуле.

Дифференцируя Е по температуре, после некоторых упрощении получим

C_V ∼ T. (XIII.34)

Таким образом, теплоемкость электронного газа при низких температурах пропорциональна температуре.

Поскольку теплоемкость решетки металла пропорциональна кубу температуры, то она стремится к нулю быстрее теплоемкости электронного газа. Поэтому при достаточно низких температурах значительная часть общей теплоемкости обязана электронам. Так, приблизительно при T = 3K для меди теплоемкости электронного газа и решетки равны друг другу. Точные измерения теплоемкости металлов при очень низких, температурах подтверждают формулу (XIII.34).

319