Всякое тело способно изучить (и, следовательно, поглощать) электромагнитные излучения определенных частот. Мы знаем, что спектр газа линейчат - это означает, что газ испускает дискретный набор частот. Конденсированные тела имеют сплошные спектры поглощения (и, следовательно, испускания).
Тело, способное поглощать все частоты, носит название абсолютно черного тела. При достаточно большом давлении всякое тело будет приближаться к абсолютно черному. Для того чтобы абсолютно черное тело не поглощало и не испускало, необходимо, чтобы пространство вокруг него было заполнено некоторым излучением, равновесным с абсолютно черным телом.
Поскольку энергия этого излучения зависит от температуры, то "пустота" имеет свою теплоемкость. При температурах порядка миллионов градусов теплоемкость "пустоты" даже больше теплоемкости твердого тела такого же объема.
Возникает вопрос о распределении энергии по частотам в этом равновесном с абсолютно черным телом излучении.
Конечно, реальное тело не является абсолютно черным, но можно показать (закон Кирхгофа), что интенсивность излучения абсолютно черного тела является верхним пределом для интенсивности излучения любого тела при заданной температуре.
Впервые задача распределения энергии в спектре абсолютно черного тела была решена в 1900 г. в классической работе Планка.
Число собственных колебаний, рассчитанное на единицу объема с учетом поляризации света
dNν = 8πν2dνc3,
где c - скорость света.
Энергию этих колебаний dUν мы получим, умножив это число на среднюю энергию одного колебания ε
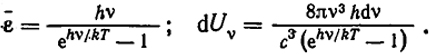(XIII.24)
Этот результат может быть получен на основе рассмотрения статистики фотонного газа.
В 1905 г. Эйнштейн предположил, что в промежутке между актами излучения и поглощения порция энергии hν существует в виде кванта энергии - фотона. Фотоны-квазичастицы
315
не подчиняются запрету. Паули и, следовательно, должны быть рассмотрены на основе статистики Бозе-Эйнштейна.
Отличие статистики фотонов от статистики частиц заключается в том, что в этом случае нет оснований требовать постоянства числа частиц.
Энергии hν фотона отвечает определенный импульс р. Поскольку фотон движется со скоростью света, то для Е и р должны применяться формулы релятивистской механики:
ε = m0c2√1 - (V/с)2;
(XIII.25)
p = m0V√1 - (V/c)2,
(XIII.26)
где m0 - масса покоя, которая для фотона должна равняться нулю, ибо только в этом случае при V = c; ε ≠ ∞. Из (XIII.25) и (XIII.26) следует, что при V = c
p = ε/c = hν/c.
Как и ранее, рассмотрим максимум
при условии ∑Niεi = E, так как число фотонов может изменяться. Находя, как и ранее, экстремум w получим
Ni = g/(eβei - 1),
(XIII.27)
где
β = l/kT, g =
2.
Коэффициент 2 в последней формуле указывает на возможность двух поляризаций излучения.
Заменяя в уравнении (XIII.27) εi на hν, а р на hν/c, мы получим вновь уравнение Планка (XIII.24).
Из уравнения Планка следуют два важных вывода.
Найдем общую энергию единицы объема излучения:
Введя x = hν/kT, получим
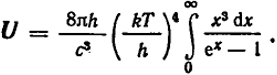
316
Ранее уже указывалось (см. гл. XII), что определенный интеграл равен π4/15.
Таким образом:
U = (8π5/15)·[(kT)4/(hc)3].
(XIII.28)
Уравнение (XIII.28) носит название закона Стефана-Больцмана.
Мы видим, что в отличие от твердого тела энергия абсолютно черного тела при любой температуре пропорциональна четвертой степени температуры, а теплоемкость, следовательно, - третьей степени температуры.
Поэтому теплоемкость единицы объема "пустоты" делается сравнимой с теплоемкостью единицы объема твердого тела при достаточно высоких температурах.
Из формулы (XIII.24) следует, что при заданной температуре имеется определенная частота (и, следовательно, длина волны), на которую приходится максимум энергии излучения.
Поскольку ν = c/λ, то
dU(λ, T) = -
dλ = π(λ,
T)dν.
Для определения λmax необходимо решить уравнение: ∂ρ/∂λ = 0, т.е.
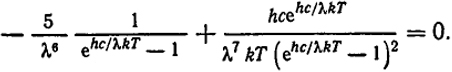
Пусть hcmax = xmax. Тогда (xmaxexmax)/(exmax - 1) = 5. Решение этого уравнения: xmax = 4,96.
Таким образом, λmaxT = 2·10-1(hc/k).
Это уравнение носит название закона смещения Вина, который является теоретической основой определения температуры по свечению тела.
317
