§ 5. Статистика Бозе-Эйнштейна и Ферми-Дирака

Уравнения статистики Больцмана были получены нами как асимптотические, правильные для высоких температур. При низких температурах в зависимости от подчинения принципу Паули, как это указывалось в гл. XI, газ описывается статистикой Бозе-Эйнштейна или статистикой Ферми-Дирака.

Рассмотрим величину термодинамической вероятности для обоих случаев.

Каким числом способов можно распределить N_i молекул по g ячейкам области при отсутствии запрета Паули? Каждое такое распределение можно описать, помещая в один ряд все молекулы и ячейки. При этом условимся, что

312

все молекулы, находящиеся между двумя ячейками, помещаются в левой. Тогда каждому распределению молекул по ячейкам будет отвечать некоторая перестановка молекул и ячеек в ряду.

Число способов, какими можно распределить N_i молекул по g ячейкам, равно числу перестановок всех этих элементов в указанном ряду. При этом необходимо учесть, что при всех таких перестановках первым элементом должна быть ячейка, так как если там окажется молекула, то вследствие отсутствия слева ячейки она окажется вне ячеек. Кроме того, нужно учесть, что перестановки между молекулами и ячейками не приведут к новым распределениям. Таким образом:

ω_i = (g + N_i - 1)!/(g - 1)!N_i!. (XIII.20)

Все частицы, состоящие из четного числа элементарных частиц, описываются этим уравнением и, следовательно, статистикой Бозе-Эйнштейна.

Для частиц, подчиняющихся запрету Паули, следует учесть, что в каждом квантовом состоянии может быть только одна частица. По принципу Паули в одной ячейке могут находиться две частицы с противоположными спинами (гл. XXI). Уменьшив объем ячейки вдвое, примем, что в каждой ячейке может находиться одна частица. Расчет числа способов размещения молекул по g ячейкам фазовой области сводится к расчету числа сочетаний C

Ni

g

  , какими могут быть из g ячеек выделены N_i.

ω_i = C

Ni

g

  = g/[(g - N_i)!N_i!]. (XIII.21)

Для перехода от выражений (XIII.20) и (XIII.21) к распределению, необходимо вычислить величину ω:

ω =

∏

i

  ω_i и S = klnω.

После применения уравнения Стерлинга соответственно для статистики Бозе-Эйнштейна получим

S = k∑(g + N_i)ln(g + N_i) - N_ilnN_i - g_ilng_i

и для статистики Ферми-Дирака

S = k∑glng - N_ilnN_i - (g - N_i)!n(g - N_i).

Учитывая условия ∑N_iε_i = E и ∑N_i = N, как и ранее при выводе распределения Больцмана, получим

N_i = g/(Ae^βε_i ± 1). (XIII.22)

313

В этом уравнении минус соответствует статистике Бозе-Эйнштейна, а плюс - статистике Ферми-Дирака.

При высоких температурах обе формулы должны перейти в формулу, описывающую распределение Больцмана:

N_i = Ne^-ε_i/kT/∑e^-ε_i/kT.

Это может произойти, если А окажется при высоких температурах настолько большим, что единицей в уравнении (XIII.22) можно будет пренебречь. Отсюда следует, что

β = 1/kT и g/A = N/∑e^-ε_i/kT.

Таким образом:

A = g∑e^-ε_i/kT/N.

Для одноатомного газа

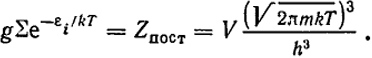
Условие перехода рассматриваемых статистик в больцмановскую запишется следующим образом:

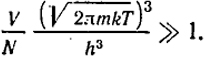(XIII.23)

Мы видим, что чем меньше масса частицы т, тем выше температура, при которой правильна статистика Больцмана.

Однако даже для водорода расчет по формуле (XIII.23) показывает, что левая часть неравенства больше правой уже при очень низкой температуре (доли градуса Кельвина).

Поэтому для всех газов уравнение Больцмана практически верно при любых температурах. Исключением является электронный газ.

Приняв, что в единице объема содержится 6·10²² электронов (что имеет место в металлах), и учитывая, что масса электрона равна 10^-31 кг, получим, что неравенство (XIII.23) выполняется для электронного газа лишь при десятках тысяч градусов.

Таким образом, электронный газ в металлах не может быть описан статистикой Больцмана и требует применения статистики Ферми-Дирака.

Фотонный газ требует применения статистики Бозе-Эйнштейна.

314