§ 4. Упругость пара твердого тела

Для расчета гетерогенных равновесий необходимо знать свободную энергию твердого тела.

Согласно (XIII.3), свободная энергия твердого тела может быть представлена как свободная энергия N_A атомной молекулы:

G = -kTln

∏

3NA

  (1 - e^-hν_i/kT)^-1.

Если принять приближение Эйнштейна и ввести среднюю частоту ν, то

G = -kTln(1 - e^-hν/kT)^-3N_A = 3RTln(1 - e^-hν/kT).

Приняв приближение Дебая, получим для низких температур (T ≪ θ):

G = (N_Aπ⁴/5)k(T/θ)⁴.

В качестве простейшего гетерогенного равновесия рассмотрим равновесие твердое тело - пар.

В разделе термодинамики было показано, что упругость пара подчиняется уравнению Клапейрона-Клаузиуса:

d ln p/dT = σ/RT²

и после интегрирования

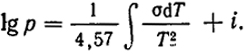
Статистический расчет должен быть абсолютным и, следовательно, привести к вычислению i.

Условие равновесия А (т) = А (пар) запишется как равенство свободных энергий

G_т = G_пар.

311

Для простоты рассмотрим случай, когда пар состоит из атомов. Тогда

G_п = -RTln[V(√2πmkT)³(2I + 1)]/Nh³.

Для расчета величины i достаточно рассмотреть область очень низких температур, при которых твердое тело полностью вырождено.

Если kT ≪ hν, Z_k ≈ 1, то G_т = 0.

Следует учесть, что уровень отсчета энергии при рассмотрении суммы состояний твердого тела ниже на теплоту возгонки при абсолютном нуле (σ₀) по сравнению с уровнем отсчета энергии в сумме состояний газа. Поэтому

-RTln[(2πmkT)³V/h³N](2I + 1) = 0 - σ₀.

Поскольку

V = RT/p,

то

(XIII.19)

Таблица XIII.2. Теоретические и опытные значения химических постоянных

Вещество	Значения
	теоретические	опытные
Ar	0,81	0.79
Ne	0,57	0,59
Hg	1,87	1,83
Pb	1,90	2,00
Cd	1,49	1,50

Третий член уравнения представляет собой химическую постоянную. в табл. XIII.2 показано, что результаты расчета хорошо согласуются с опытом.

312