§ 3. Расчет химического равновесия

Вычисленные статистическими методами термодинамические функции могут быть использованы для расчета химического равновесия по формулам гл. III.

Однако представляет интерес, непосредственный расчет константы равновесия по спектроскопическим данным.

Рассмотрим реакцию A + 2B = D.

Условие равновесия

-G_A - 2G_B + G_D = 0

или, учитывая формулу (XIII.3):.

RTln

ZA

NA

  + 2RTln

ZB

NA

  - RTln

ZD

NA

  = 0,

или

Z_DN

2

A

  /Z_AZ

2

B

  = 1. (XIII.12)

Здесь Z содержит объем в качестве множителя. Поэтому положим

Z_i = P_iV_i,

где P_i носит название функции распределения.

Исключив Z из уравнения (XIII.12) и учитывая, что концентрация c_i равна

NA

Vi

  , получим

c_D/c_Ac²_B = P_D/P_AP²_B

Таким образом:

K_c = P_D/P_AP²_B. (ХIII.13)

При расчете функций распределения для разных молекул используются разные уровни отсчета энергии. Для учета этого обстоятельства, в соответствии с уравнением

309

(XIII.4), необходимо умножить правую часть уравнения (XIII.13) на е^-ΔE/RT, где ΔE - разность уровней отсчета.

Поскольку за нулевой уровень при расчете сумм состояний принимается энергия молекул при абсолютном нуле, то ΔE = -Q₀,

где Q₀ - теплота реакции при абсолютном нуле.

Таким образом, вместо уравнения (XIII.13) получим

K_c = (P_D/P_AP

2

B

  )e^Q₀/RT. (XIII.14)

В качестве простейшего примера рассмотрим реакцию диссоциации иода при T = 1073 K:

I₂ = 21. (XIII.15)

Согласно уравнению (XIII.14) константа равновесия этой реакции определяется уравнением

K_c = (P

2

I

  /P_I2)e^Q₀/RT (XIII.16)

Исследование спектров атомного и молекулярного иода позволяет определить постоянные, необходимые для расчета К_c по формуле (XIII.16).

Для определения функции распределения атома иода надо знать лишь атомную массу иода (А) и величину общего момента атома:

A = 126,92; I→ = 3/2.

Для расчета функции распределения молекулы иода надо знать ее момент инерции I и частоту колебания ν:

I = 7,51·10^-38 г·см²; ν = 6,39·10¹² c^-1.

Теплота реакции диссоциации иода при абсолютном нуле равна ∼ 150 кДж/моль.

Согласно уравнению (XIII.16), при учете уравнений § 2 этой главы

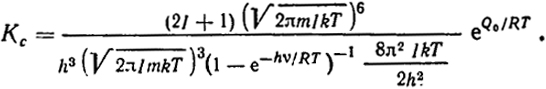(XIII.17)

Подставив вышеприведенное значение, получим величину K_с при T = 1073К:

K_c = 7,46·10¹⁶. (XIII.18)

В соответствии с выводом уравнения (XIII.14), концентрации в этом уравнении выражены в молекулах на кубический сантиметр.

310

Для перевода этих концентраций в обычное их измерение (моль на литр) выражение (XIII.18) надо умножить на 10³ N_A, а для перевода в K_p - умножить на RT.

Таким образом, получим:

K_p =

7,46·1016·103RT

NA

  = 7,46·10¹⁶·10³kT = 1,1·10^-2 атм.

Зависимость изменений постоянной равновесия K диссоциации иода от температуры указывает на близость экспериментальных и расчетных величин:

T, K . .	1274	1173	1073	973
Kp, атм	1,68·10-1	4,80·10-2	1,09·10-2	1,80·10-2

311