§ 2. Расчет сумм состояний

Из описанного выше следует целесообразность расчета сумм состояний для отдельных видов движения.

При расчете суммы состояний для поступательного движения (Z_пост) необходим переход от суммирования к интегрированию

303

ввиду непрерывности изменения энергии. Для этого следует перейти от суммирования по ячейкам к суммированию по областям:

Z_пост = ∑e^-ε_i/kT = g

∑

обл

  e^-ε_i/kT,

где

g = ΔxΔyΔzΔp_xΔp_yΔp_z/h³.

Таким образом:

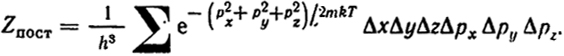
Перейдя в пределе к интегралу, получим

откуда

Z_пост = (υ/h³)(√2πmkT)³ (XIII.5)

Для двумерного газа

Z_пост = (s/h²)(√2πmkT)²,

где s - поверхность, занимаемая молем адсорбированного газа.

При рассмотрении вращательной суммы состояний для всех случаев, кроме водорода, при низких температурах, как это указывалось выше, можно также считать энергию меняющейся непрерывно и проводить интегрирование вместо суммирования.

Рассмотрим случай одномерного вращения (изменяется лишь один угол φ):

Z_вр = ∑e^-ε_i/kT = (ΔφΔp/h)∑e^-ε_i/kT.

Поскольку для одномерного вращения

ε = p²/2J,

то

(XIII.6)

Для двумерного вращения (изменяются два угла), которое

304

имеет место, например, для двухатомной молекулы, такое суммирование следует провести по двум углам, используя сферические координаты.

Опустим вывод и сразу напишем результат:

Z_вр = 8π²IkT/h². (XIII.7)

Этот результат с точностью до постоянной можно было бы получить, возведя выражение (XIII.6) для одномерного вращения в квадрат.

Следует, однако, при суммировании, проводимом при выводе уравнения (XIII.6), учесть неотличимость атомов так же, как мы ранее учитывали неотличимость молекул.

Каждому положению двухатомной симметричной молекулы соответствует другое идентичное положение, в которое она может быть переведена путем вращения. Таким образом:

Z_вр = 8π²/σh²,

где σ - число симметрии, показывающее, сколькими способами молекула может быть совмещена сама с собой путем вращения.

Из описанного выше следует, что σ = 1 для несимметричных молекул и σ = 2 для двухатомных симметричных молекул.

Как указывалось, вращение сколь угодно сложной молекулы описывается как изменение трех углов. Соответствующее суммирование по трем углам приводит к выражению

Z_вр = (√π/σh³)(8π²kTI₁I₂I₃)³

где I₁, I₂, I₃ - три момента инерции сложной молекулы; σ - число симметрии.

Молекула аммиака представляет собой пирамиду, в основании которой находятся три атома водорода и, следовательно, σ = 3. Для метана σ = 12, так как мы можем совершать по три вращения вокруг каждой из четырех связей С—Н.

При рассмотрении суммы состояний колебательного движения следует учитывать, что энергия меняется скачкообразно, и не производить замену суммирования интегрированием:

∑_кол =

∑

яч

  e^-ε_i/kT.

305

Ранее было показано, что ε = nhν, тогда

Z_кол =

∑

n

  e^-nhν/kT = (1 - e^-hν/kT)^-1

При высоких температурах kT ≫ hν. Проведя соответствующее разложение, получим

Z_кол = kT/hν. (XIII.9)

Этот результат мог бы быть получен заменой суммы интегралом аналогично приведенным выше расчетам для поступательного и вращательного движения.

Как указывалось, r-атомная молекула имеет 3r - 6 независимых колебаний.

В соответствии с тем, что сумма состояний сложного движения равна произведению сумм состояний для отдельных видов движения:

Z_кол =

П

3r - 6

  (1 - e^-hν_i/kT)^-1

Для расчета суммы состояний r-атомной молекулы нужно знать частоты всех ее 3r - 6 колебаний.

Существование 3r - 6 собственных колебаний молекулы означает, что любое сложное колебание ее атомов может быть разложено на 3r - 6 составляющих простых независимых колебаний. В каждом таком простом колебании участвует, конечно, не один атом, а определенные группы атомов.

Для расчета Z_кол нет необходимости определять, как осуществляются различными атомами рассматриваемые колебания; надо знать лишь их частоты.

Спектр молекул непосредственно дает все Зr - 6 колебаний.

При расчете электронной суммы состояний (Z_эл) следует учесть, что каждое состояние с энергией ε_i характеризуется определенным статистическим весом g_i, т.е. числом способов (квантовых состояний), какими эта энергия может проявляться. Поэтому

Z_эл = g₀e^-ε₀/kT + g₁e^-ε₁/kT + ... . (XIII.10)

Энергия основного состояния ε₀ обычно принимается за нуль. Расчет Z_эл облегчается тем, что электронные кванты (расстояния между уровнями) обычно велики (значительно больше kT).

Поэтому в уравнении (XII. 10) при обычно рассматриваемых температурах можно пренебречь всеми членами,

306

кроме первого. Таким образом,

Z_эл = g₀.

Для определения g₀ необходимо рассмотреть причины существования ряда квантовых состояний с одинаковой энергией.

Рассмотрим этот вопрос для наиболее простого случая - атома.

Как это будет подробнее рассмотрено в части IV (гл. XXI), каждый электрон в атоме обладает определенным моментом орбитального движения (орбитальным моментом) и моментом собственного вращения (спин-моментом).

Векторная сумма всех орбитальных моментов составляет общий орбитальный момент атома L→, а сумма всех спин-моментов - результирующий спин-момент атома S→. Общий момент атома I_i→ определяется как векторная сумма этих моментов:

I_i→ = L→ + S→.

Все моменты здесь выражены в единицах h/2π.

Каждый энергетический терм ε_i характеризуется определенным значением этого общего момента I_i→.

В отсутствие внешнего поля энергия атома не будет зависеть от ориентации этого момента. Таким образом, одной энергии атома отвечают различные ориентации I_i→, что и определяет статистический вес терма g.

Согласно законам квантовой механики, не все ориентации момента по отношению к какой-нибудь оси разрешаются. Возможны лишь такие ориентации, при которых значения проекций момента будут отличаться на единицу.

Таким образом, проекции момента I_i могут иметь следующие значения:

-I_i; -I_i + 1; ... ; 0; 1; 2; ... ,I_i.

Поэтому число проекций составляет

2I + 1,

и, следовательно:

g₀ = 2I₀ + 1

Величина I₀ может быть получена из спектра атомов.

Рассмотренный метод расчета сумм состояний называют методом расчета по значениям молекулярных постоянных. Из спектров атомов и молекул получают необходимые

307

характеристики и по указанным формулам определяют Z.

Отметим, что наряду с этим методом существует так называемый метод непосредственного суммирования, при котором непосредственно из спектра определяют значения энергии молекулы (ε_i) и статистические веса и получают Z путем суммирования.

В качестве примера статистического расчета термодинамических функций рассмотрим величину энтропии одноатомного газа.

Из основных формул термодинамики (гл. II) было показано, что для идеального газа

S = C_V ln Т + R ln υ + С.

Расчет не был абсолютным, так как величина постоянной С определялась из опытных данных.

Формулы статистической механики позволяют провести абсолютный расчет.

Для одноатомного газа

Z = (2I + 1)(υ/h³)(√2πmkT)³.

Подставив эту величину в уравнение (XIII.2), получим

S =

E

T

  + R ln

(2I + 1)υe(√2πmkT)3

Nh3

  .

Учитывая, что для одноатомного газа Е = 3/2RT, получим

S =

3

2

  R ln T + R ln υ +

3

2

  R + R ln

(2j + 1)(2πmk)3

Nh3

  . (XIII.11)

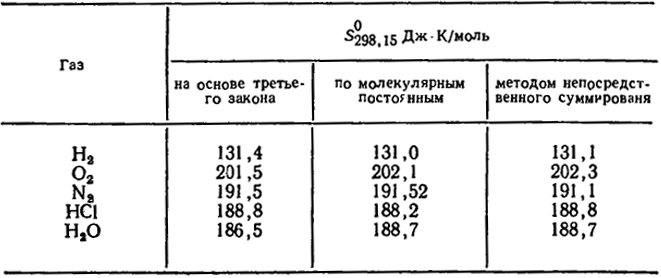
Таблица XIII.1. Значения стандартных величин энтропии, рассчитанные из термических величин и спектроскопических данных

308

Эта формула позволяет провести абсолютный расчет энтропии.

Очевидно, что аналогичные формулы могут быть выведены и для многоатомных газов.

Точность подобных расчетов может быть проиллюстрирована табл. XIII.1, в которой приведены результаты расчета стандартных значений энтропии ряда газов, полученных на основе третьего закона термодинамики (гл. IV), на основе молекулярных постоянных и методом непосредственного суммирования.

309