Русский академик Г.И. Гесс выполнил большое число калориметрических опытов и определил теплоты нейтрализации многих кислот аммиаком и щелочами. Приведем один пример.
Раствор хлористого аммония в воде можно приготовить двумя путями: из газообразных НСl и NH3 получают твердый NH4C1, который затем растворяют в воде; каждый из указанных газов в отдельности растворяют в воде и полученные растворы сливают для нейтрализации.
Г.И. Гесс установил, что суммы тепловых эффектов реакций, осуществляемых этими двумя различными путями, равны между собой и, основываясь на ряде подобных результатов, в 1840 г. сформулировал закон: тепловой эффект химической реакции определяется только природой, а также состоянием исходных веществ и продуктов реакции и не зависит от того, по какому пути протекает данный процесс и какие промежуточные вещества при этом образуются.
Очевидно эта формулировка непосредственно следует из первого закона термодинамики, так как в указанных двух случаях (р или V постоянны) величины Qp и Qv совпадают с изменениями функций состояния Н и U. Интересно, однако, отметить, что закон Гесса был открыт раньше, чем был ясно сформулирован и получил признание первый закон термодинамики.
Приведем примеры, иллюстрирующие этот закон.
1. Железо, реагируя с кислородом, может сразу образовать высший оксид:
2Feт + 3/2О2Г = Fe2O3T + 821,3 кДж/моль.
(а)
26
2. Эта же реакция может протекать и с образованием промежуточного продукта - FeO и последующим его окислением до Fe2O3:
2Feт + O2Г = 2FeOт + 2·265,5 кДж/моль;
(б)
2FeOт + 1/2О2Г = Fe2O3т + 290,3 кДж/моль.
(в)
Согласно закону Гесса теплота реакции одинакова независимо от того, превратились ли исходные вещества сразу в продукты реакций или при этом происходило образование промежуточных веществ. Соответственно теплота образования одного моля Fе2O3 из простых веществ (элементов) должна быть равна сумме теплот образования двух молей FeO и теплоты их окисления до Fe2O3, как это видно из приведенных данных.
При вычислениях с использованием закона Гесса можно оперировать термохимическими уравнениями, как алгебраическими. В рассматриваемом случае сложим два термохимических уравнения (б) и (в), умножив при этом первое на 2. Их сумма эквивалентна термохимическому уравнению (а):
2Feт + О2Г = 2FeOт + 2·265,5 кДж/моль;
2FeOт + 1/2O2Г = Fе2O3т + 290,3 кДж/моль;
2Feт + 3/2O2Г = Fe2O3т + 821,3 кДж/моль.
В приведенных термохимических уравнениях тепловой эффект реакции записан в их правой части со знаком +. Это соответствует исторической традиции, которая рассматривала процессы применительно к человеку и выделение тепла считала положительным. В современной термодинамике принята противоположная система знаков, в которой процессы рассматриваются исходя из состояния системы. При экзотермических реакциях энтальпия системы уменьшается и, следовательно, величина ΔH имеет знак -, а при эндотермических реакциях изменение энтальпии считается положительным.
В термохимических уравнениях обозначения в скобках указывают агрегатное состояние вещества: τ - твердое, ж - жидкость, г - газ и р-р - вещество находится в растворе. Это очень важно, так как величина теплового эффекта одной и той же реакции зависит от того, в каком состоянии находятся реагирующие вещества и продукты реакции. Например, при соединении водорода и кислорода с образованием жидкой воды выделится тепла больше, чем при образовании пара. Разность равна величине теплоты испарения воды.
Обычно в термохимических уравнениях, если это специально не оговаривается, используют величины ΔH.
Из приведенного выше примера видно, что с помощью закона Гесса можно вычислить теплоту какой-либо реакции без ее непосредственного измерения, если известны теплоты реакций, комбинированием которых она может быть представлена. Это важно для таких реакций, которые трудно осуществить в калориметре. Например, практически невозможно измерить теплоту процесса превращения графита в алмаз, осуществляемого в настоящее время в промышленных масштабах. Однако можно с большой точностью определить теплоты сгорания графита и алмаза с образованием углекислого газа и по ним вычислить теплоту превращения.
Запишем термохимические уравнения этих реакций;
Страфит + О2Г = СО2Г + ΔH1;
Салмаз + О2Г = СО2г + ΔH2,
где ΔH1 = -393,51 кДж/моль и ΔH2 = -395,41 кДж/моль.
27
Вычитая из верхнего уравнения нижнее, получим:
Cграфит - Салмаз = ΔH1 - ΔH2
или
Сграфит = Cалмаз + AR, - АR2 = - 393,51 - (- 395,41) = = 1,90 кДж/моль.
Следовательно, превращение графита в алмаз сопровождается поглощением тепла.
Обобщая этот результат, отметим, что теплота реакции может быть найдена как разность между теплотами сгорания исходных веществ и продуктов реакции, т.е. ΔHреакции = Δ (ΔHсгорания). Как и ранее, для записи этой разности используется символ Δ. Это правило, особенно необходимое для органической химии; указывает на целесообразность составления таблиц теплот сгорания различных веществ. Такие таблицы отвечают общему требованию, так как в них должны присутствовать характеристики, относящиеся к веществам, а не к реакциям. Вместе с тем выбор для табулирования теплот сгорания имеет и существенные недостатки. В калориметрическом опыте далеко не всегда удается достичь одной и той же степени окисления продуктов сгорания. Измерения этих теплот получили значение в термохимии лишь вследствие относительной простоты соответствующих опытов, а не потому, что они дают более важные характеристики, чем теплоты других реакций.
Какие же величины целесообразно выбрать для составления термохимических таблиц? Остановимся на этом важном вопросе.
Так как большинство процессов протекает при постоянном давлении, то такие таблицы целесообразно составлять для энтальпий. Вообще говоря, при вычислении изменения энтальпии при реакции (ΔH) не имеет значения, какое состояние принято за начало отсчета (так называемое стандартное состояние). Наиболее удобно, однако, в качестве стандартного состояния выбрать состояние простых веществ (элементов) при 25° C (298 К) и нормальном атмосферном давлении. Если какое-либо вещество существует в нескольких модификациях, то в качестве стандартного состояния принимают ту модификацию, которая является устойчивой при 25° C и атмосферном давлении.
Таким образом, энтальпии простых веществ в стандартном состоянии условно принимают равными нулю и записывают нижним индексом, обозначающим температуру, и верхним индексом 0, указывающим на атмосферное давление. При таких обозначениях термохимическое уравнение,
28
например, для реакции образования жидкой воды H2г + 1/2O2г = H2Oж имеет вид
ΔH
=
H
-
H
- 1/2
H
= -285,84 кДж/моль.
Так как по условию H
и
Н
равны нулю, то Δ
H
=
H
. Эта относительная энтальпия воды называется энтальпией образования и дополнительно снабжается нижним индексом
f (от английского слова formation) - Δ
H
.
Стандартные энтальпии образования соединений из простых веществ помещают в специальных таблицах термодинамических величин, которые публикуются в справочниках. В табл. 1.1 для иллюстрации приведены некоторые извлечения из таких справочников. Наряду со значениями ΔH
таблицы содержат величины Δ
G
-энергий Гиббса образования соединений также из простых веществ и
S
- абсолютных энтропии веществ и соединений. Величины
G и
S являются функциями состояния, вытекающими из второго закона термодинамики, содержание которого излагается в следующей главе. Из табл. 1.1 видно, что в соответствии с выбранным стандартным состоянием величины Δ
H
для простых веществ равны нулю. Если вещество находится не в стандартном состоянии (например, водород в атомарном состоянии), то Δ
H
есть положительная величина, равная энергии, затрачиваемой на диссоциацию молекул Н
2. Для неустойчивых модификаций веществ в твердом состоянии значения Δ
H
тоже положительны, так как их перевод из устойчивого состояния сопровождается затратой тепла. Большинство соединений образуется с выделением тепла, и соответственно величины Δ
H
отрицательны. Лишь для немногих эндотермических соединений, например, NO, C
2H
2, Δ
H
положительны. Любую реакцию можно рассматривать как совокупность процессов разложения исходных соединений на простые вещества и образования из них новых соединений. Поэтому из закона Гесса следует, что величина Δ
H
при любой реакции равна алгебраической сумме величин Δ
H
для всех участников реакции:
ΔH
= Δ(ΔH)i,
(I.26)
где i - индекс вещества.
29
Таблица 1.1. Стандартные термодинамические величины некоторых веществ и энергии связи
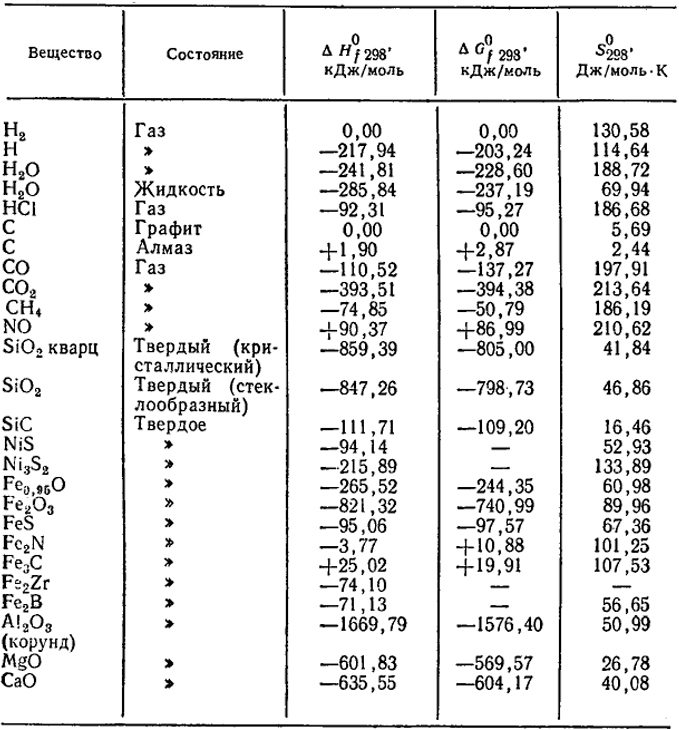
В качестве примера приведем расчет ΔH
для реакции: Fe
2O
3т + 3CO
г = 2Fe
т + 3СО
2Г;
ΔH
= 3Δ
H
- 3Δ
H
- Δ
H
= 3(-393,5) - 3(-110,5) – (-821,3) = 27,6 кДж/моль, поскольку Δ
H
= 0.
Наряду с энтальпиями образования соединений из простых веществ представляют интерес величины энергий связи между атомами в молекулах:
| Связь |
H - H |
H - N |
H - O |
H - C |
| ΔH
кДж/моль |
435,88 |
390,79 |
462,75 |
413,38 |
30
Продолжение
| Связь |
С - О |
С = С |
N ≡ N |
| ΔH
кДж/моль |
351,46 |
606,68 |
945,58 |
Напомним, что табличные величины ΔH
характеризуют энтальпии образования соединений их простых веществ в стандартном состоянии, а не теплоты образования соединений из атомов. Так, например, энтальпия образования метана из простых веществ
Cграфит + 2Н2г = СН4г,
(а)
составляющая 74,85 кДж/моль, не равна энергии, которую необходимо затратить на отрыв четырех атомов водорода от атома углерода. Разница состоит в том, что во втором случае следует учесть и энергию образования (диссоциации) молекул из атомов, как это можно видеть, если просуммировать уравнение (а) со следующими*
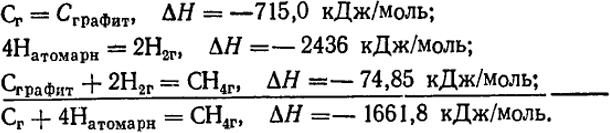
В этих уравнениях используются еще две величины - теплоты, затрачиваемой на сублимацию одного моля графита или выделяющейся при его конденсации из газа 715,0 кДж и теплоты образования молекулярного водорода из атомов 436 кДж. Найденная величина 1661,8 кДж намного больше теплоты образования метана из элементов, что обусловлено значительно большим запасом энергии у атомов по сравнению с молекулами. Эта величина представляет собой энергию, которую надо затратить, чтобы разъединить молекулу метана на атомы (такие величины называются теплотами атомизации). Так как в метане, структурная формула которого имеет вид 
, все связи С - Н равноценны, то из найденной величины можно вычислить энергию одной такой связи, т.е. 1661,8 : 4 ≈ 415 кДж. Таким путем могут быть найдены энергии и других связей в молекулах органических соединений, например энергия связи С - С в этане, имеющем структурную формулу
31
Расчет основан на предположении о том, что во всех предельных углеводородах энергии связей С - Н и С - С одинаковы и что энергия связи молекулы аддитивно складывается из соответствующих величин отдельных связей.
Из термодинамических данных следует, что энтальпия образования этана из атомов равна приблизительно 2816 кДж. Вычитая из этой величины энергию шести связей С - Н, т.е. 415·6 = 2490 кДж, найдем, это энергия связи С - С составляет ∼ 326 кДж. Предположение об аддитивности связи в соединениях ряда предельных углеводородов подтверждается хорошим совпадением вычисленных значений с величинами, найденными из опыта для высших гомологов, например пропана (С3Н8). Данные об энергиях связи (некоторые из них приведены в табл. 1.1) позволяют проводить различные оценки, в частности вычисления теплот реакций, которые равны разности между энергиями разрываемых связей и вновь образующихся. Например, для реакции гидрирования этилена:
ΔH
= [(Н - Н) + (С = С)] - [2(С - Н) + (С - С)] = 436 + 607 - 2·415 - 326 = -213 кДж.
Из сказанного в настоящем разделе видно, что при использовании таблиц стандартных величин тепловые эффекты определяют по разности больших величин (например, теплоту превращения графит - алмаз). Даже сравнительно небольшие погрешности при измерениях тепловых эффектов могут привести к большим ошибкам в значениях вычисляемой теплоты. В связи с этим в современной калориметрии разработаны методы, позволяющие проводить измерения с очень высокой степенью точности. Так, теплоты сгорания определяются с точностью до 0,01 %. Дифференциальные калориметры, использующие электрические способы измерения температуры, дают возможность измерять количества тепла с точностью до 10-5 Дж.
32
