Глава XIII

РАСЧЕТ ТЕРМОДИНАМИЧЕСКИХ ФУНКЦИЙ

§ 1. Сумма состояний

Статистическая механика не только дает обоснование термодинамическим методам расчета, но и позволяет связать термодинамические характеристики с микроскопическими. Из уравнения (XI.5) после подстановки B₁ = 1/kT и простых преобразований получим:

300

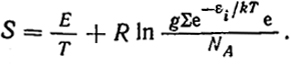
Величина Z = g

∑

обл

  e^-ε_i/kT носит название суммы состояний (индекс "обл" под знаком ∑ означает, что суммирование производится по областям). Суммирование по областям и умножение на число ячеек равносильно суммированию по ячейкам. Таким образом:

Z = ∑e^-ε_i/kT; (XIII.1) S =

E

T

  + Rln(Ze/N_A); (XIII.2)

A = E - TS = RTln(Ze/N_A).

При рассмотрении статистики Гиббса мы ввели сумму состояний системы Q.

Z является суммой состояний молекулы.

Определим связь суммы состояний Q и Z для идеального гааа. В этом случае энергия системы складывается из энергий отдельных молекул: 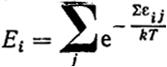, где j - индекс суммирования молекул. Тогда:

Однако при таком расчете мы считаем молекулы различными и поэтому каждое слагаемое в сумме считаем N! раз.

Таким образом:

Q =

ZN

N!

  .

Из уравнения A = U - TS следует, что

А = Е - TS = -kT ln ∑е-

Ei

kT

  .

Расчет термодинамических функций любой реальной системы сводится к расчету суммы состояний Q.

Точно так же термодинамические свойства идеальных газов могут быть выражены через сумму состояний согласно (XI1I.2).

A = E - TS = RTln

Ze

N

  .
G = А + pυ = -RT ln (Ze/N_A) + RT = - RT ln (Z/N_A). (XIII.3)

301

Для определения Е продифференцируем по температуре уравнение (XIII.1):

dZ/dT = ∑-ε^_i/kT(ε_i/kT²).

Разделив это уравнение на уравнение (XIII.1), получим

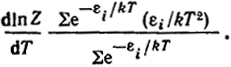
По определению

Таким образом:

ε = kT²(d ln Z/dT)

и

E = RT²(d ln Z/dT).

Мы видим, что все термодинамические функции выражаются через сумму состояний. Для того чтобы понять смысл этой характеристики, определим, сколько молекул находится в некотором состоянии j, включающем ряд областей фазового пространства:

N_j = ∑_jN_i.

Использовав для N_i формулу Больцмана, получим

N_j =

N∑je-εi/kT

∑e-εi/kT

 

Отношение чисел молекул в двух состояниях j и k определяется следующим образом:

Nj

Nk

  =

∑je-εi/kT

∑ke-εi/kT

 

Сумма по областям так же неопределенна, как и величина области. Поэтому целесообразно перейти к суммированию по ячейкам. Умножив числитель и знаменатель полученного выражения на g, найдем

N_j/N_k = Z_j/Z_k.

Таким образом, сумма состояний определяет число молекул в данном состоянии или, другими словами, тенденцию

302

молекулы проникнуть в данное состояние. Понятно, что S растет, a F и G убывают с увеличением Z. Расчет термодинамических функций сводится к расчёту суммы состояний.

Рассмотрим два свойства суммы состояний. Если энергия молекулы равна сумме энергий отдельных видов движения, то сумма состояний равна произведению сумм состояний для этих видов движения.

Действительно, пусть

ε = ∑ε_j,

где j - индекс суммирования видов движения.

Тогда

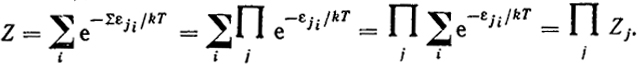
Таким образом:

Z = Z_постZ_врZ_колZ_эл

и расчет суммы состояний сводится к расчету суммы состояний отдельных видов движения.

Поскольку энергия ε зависит от уровня отсчета, то и значение Z зависит от этого уровня.

Как изменится Z при перемене уровня отсчета энергии на величину ε₀?

Пусть величина энергии молекулы, отсчитанная от нового уровня, составит ε′, тогда

ε = ε₀ + ε′

Следовательно:

Таким образом:

Z′ = Ze^ε₀/kT (XIII.4)

Уровень отсчета е определяет уровень отсчета F, G и Е, рассчитанных по величине Z. Величина S не зависит от уровня отсчета энергий, принятого при вычислении Z.

303