§ 2. Квантовая теория теплоемкости

Одним из выражений квантовых законов, как указывалось, является дискретность уровней энергии. Рассмотрим в качестве примера гармоническое колебание осциллятора: Энергия классического гармонического осциллятора может непрерывно изменяться. Эта энергия равна γA²/2 (наибольшее значение потенциальной энергии при х = А). Упругая постоянная γ - величина постоянная для данного осциллятора, а амплитуда А может изменяться непрерывно. Из данной выше формулировки квантовой механики, утверждающей дискретность фазового пространства и устанавливающей величину фазовой ячейки, следует, что

295

энергия тела, совершающего периодическое движение, например осциллятора не может изменяться непрерывно.

Мы видели, что отображающая точка, описывающая колеблющуюся частицу, движется по эллипсу. Площадь, ограниченная эллипсом, должна выражаться через целое число площадей фазовых ячеек, являющихся наименьшими "кирпичами" фазовой площади. Другими словами:

∫pdq = nh, (XII.2)

где п - так называемое квантовое число.

Эта формулировка квантовой механики, соответствующая введению фазовых ячеек, была дана Бором и Зоммерфельдом.

Если периодическое движение совершается в нескольких измерениях, то следует установить несколько таких условий для каждого измерения:

∫p_idq_i - n_ih.

Из уравнения (XII.2) вытекает в качестве следствия дискретность энергии.

Действительно, для случая осциллятора интеграл в уравнении (XII.2) передает площадь эллипса. Площадь эллипса равна πab, где а и b - полуоси эллипса.

Из уравнения (XI.1) следует, что

а = А и b = 2πmAν,

поэтому, в соответствии с уравнением (XII.2):

2π²mνA² = nh.

Учитывая, что энергия осциллятора выражается уравнением ε = γA²/2, а связь между частотой и упругой постоянной γ - уравнением

ν = (1/2π)√γ/m, (XII.3)

получим

ε = nhν. (XII.4)

Таким образом, из дискретности (квантования) фазового пространства следует дискретность (квантование) энергии.

Мы видим, что спектр энергии осциллятора характеризуется уровнями, находящимися на расстоянии hν друг от друга.

Следует отметить, что формулировка Бора и Зоммерфельда не является полной. Позднее мы рассмотрим более строгую формулировку законов квантовой механики.

296

Точная формула для энергии гармонического осциллятора оказывается несколько отличной от уравнения (XII.4), а именно:

ε = (n + l/2)hν. (XII.5)

Мы видим, что расстояние между уровнями снова равно hν.

Отличие заключается в положении уровней. Формула (XII.4) дает для низшего уровня (при n = 0) ε = 0, а по формуле (XII.5) ε = hν/2.

Однако наличие этой "нулевой" энергии означает лишь изменение уровня отсчета.

В энергии газа имеется постоянная, не зависящая от температуры часть, включающая энергию электронов. В это слагаемое можно включить "нулевую" энергию. Поэтому в дальнейших расчетах мы будем пользоваться формулой (XII.4).

Дискретность уровней, конечно, должна сказаться на величине средней энергии колебания (ε).

Определим для одного гармоннческого колебания

ε =

∑

n

  N_nnhν/N,

где N_n - число осцилляторов, находящихся на уровне n; N - общее число осцилляторов.

Согласно уравнению (XI.18)

Следовательно:

(XII.6)

и

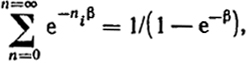(XII.7)

согласно закону суммирования членов бесконечно убывающей прогрессии. Сумму, находящуюся в числителе выражения (XII.6), можно получить, дифференцируя уравнение (ХII.7) по β, т.е.

∑ne^-nβ = e^-β/(1 - e^-β)².

Следовательно:

ε = hν/(e^hν/kT - 1). (XII.8)

297

Только в пределе при высоких температурах (kT ≫ hν), выполняется для средней энергии закон распределения.

Разлагая выражение в знаменателе в ряд и ограничиваясь одним членом, получим ε = kT.

Колебательная энергия моля двухатомного газа выразится следующим образом:

E = N_Ahν/(e^hν/kT - 1),

а его теплоемкость

При высоких температурах (kT ≫ hν)

C_Vкол → R

в соответствии с законом распределения по степеням свободы. При T ≫ 0 C_V ≫ 0.

Мы видим, что, зная частоту колебания молекулы газа, можно рассчитывать его теплоемкость.

Грамм-атом твердого тела имеет, как указывалось, 3 N колебаний. Эйнштейн приближенно принял, что частота этих колебаний одинакова. Тогда

C_{Vтв.тела} = 3С_Vкол.

Однако для твердого тела такое приближение является грубым, и передавая факт уменьшения теплоемкости с понижением температуры, неправильно описывает закон этого уменьшения.

Физический смысл этого приближения можно понять на основе так называемой "ячеечной" модели твердого тела, которой мы не раз будем пользоваться в дальнейшем. По этой модели для каждого атома твердого тела остальные атомы создают некоторое потенциальное поле, в котором он движется. В рамках такого представления все атомы находятся в одинаковом поле и движутся независимо друг от друга.

На самом деле притяжение данного атома к соседним зависит от их мгновенного положения, поэтому "ячеечная" модель является лишь грубым приближением. Поэтому частоты 3 N колебаний твердого тела различны. Для определения теплоемкости твердого тела надо знать спектр его колебаний, т.е. функцию f(ν):

dn_ν = f(ν)d ν

298

dn_ν - число колебаний, имеющих частоту от ν до ν + dν. Тогда колебательная энергия твердого тела выразится следующим образом:

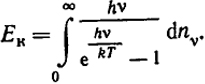
В теории теплоемкости твердого тела Дебая дается приближенный способ определения f(ν), идея которого заключается в временном отказе от атомной структуры твердого тела, рассматриваемого как непрерывное. Мы знаем, что струна имеет определенный спектр собственных частот. Точно так же и непрерывное твердое тело имеет спектр собственных частот. Однако, число таких частот как у струны так и объемного твердого тела равны бесконечности. Между тем атом твердого тела имеет 3 N_A колебаний. Целесообразно отобрать колебания, для которых принятое приближение дает меньшую ошибку. Осуществить волны очень малых длин (сравнимые и меньшие периода решетки) в твердом теле невозможно. Поэтому принятое приближение будет неверно передавать волны малых длин, т.е. большие частоты. Поэтому в теории Дебая отбирается 3 N_A частот от ν = 0 до ν = ν_max, так чтобы п = 3 N_A.

Такой расчет приводит к следующему выражению:

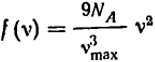
и соответственно

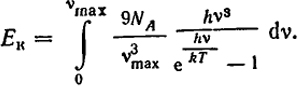(XII.10)

Приближенная теория имеет смысл при наличии оценки ошибки или если приближение асимптотически верно для определенной области опыта.

Так как колебания с большей частотой при низких температурах из-за большего кванта hν вырождены и не участвуют в температурном движении, теория Дебая асимптотически верна при низких температурах.

В этой области уравнение (XII.10) переходит в уравнение

299

и соответственно

(XII.11)

Закон кубов прекрасно выполняется для твердых тел при низких температурах. Из уравнения (ХII.11) видно, что C_V/R выражается через безразмерную величину T/θ носит название характеристической температуры. Чем выше характеристическая температура, тем выше лежит область температур, где вырождение не имеет место.

Теплоемкость, соответствующая вращению молекул газов, также должна быть рассмотрена на основе квантовой теории.

Однако, как указывалось выше, практически при всех температурах для всех газов, кроме водорода, вращательная теплоемкость правильно описывается законом распределения по степеням свободы. Поэтому квантовая теория вращательной теплоемкости представляет интерес лишь при рассмотрении теплоемкости водорода.

Почему температура, при которой вырождается вращательное движение, существенно ниже, чем для колебательного движения?

Из формулы (XII.8) следует, что чем меньше колебательный квант (расстояние между уровнями), тем ниже температура, при которой выполняется закон распределения.

Квант вращательной энергии существенно меньше, чем колебательной. Поэтому температура, при которой вырождается вращательное движение, настолько низка, что газ раньше конденсируется.

300