Как указывалось, статистика Больцмана правильна лишь при идеальных газах и справедлива для высоких температур. Кроме того, при использовании формул этой статистики мы полагали в соответствии с классической механикой, что энергия молекулы изменяется непрерывно. Между тем в главе IV уже указывалось, что квантовая механика приводит к дискретному набору уровней атомной системы. Описывать такие системы целесообразнее на основе статистики Гиббса. Таким образом более общей статистикой, верной для любых систем и условий, является статистика Гиббса. Особенно важно, что она описывает реальные системы при наличии взаимодействия молекул.
Статистика Больцмана - статистика молекул. Статистика Гиббса - статистика систем. Действительно, при наличии взаимодействия свойств молекул отдельных компонентов утрачиваются. Можно вводить и в рамках статистики Больцмана парциальные величины, изменяя в уравнении (XI.6) εi на парциальную εi, отвечающую изменению энергии системы при введении в i-тую область фазового пространства еще одной молекулы.
Наиболее целесообразное рассмотрение реальных систем дает статистика Гиббса. В этой статистике вводится понятие ансамбля систем. Каждая система представляет собой весьма сложное механическое тело, способное находиться в определенных состояниях. Пусть энергия системы в этих состояний задается набором значений Еi.
В рассматриваемом ансамбле имеется большое число одинаковых систем. Ансамбль замкнут и, следовательно, обладает заданным общим запасом энергии. Отсюда, конечно, не. следует, что задается энергия кaждoй системы - члена ансамбля. Будем полагать, что энергия ансамбля, аддитивно складывается из энергий отдельных систем. Это значит, что между системами нет каких-либо действующих сил. Однако допустим, что системы могут обмениваться энергией, передавать ее друг другу, например, путем излучения.
291
Можно, однако, вместо фотонного газа представить себе, что между системами в ансамбле находится какой-либо разреженный газ, практически не имеющий энергии, но способный передавать ее от одной системы к другой. В таком ансамбле энергия каждой системы не будет фиксирована. Благодаря обмену энергией каждая система будет некоторым образом изменять свою энергию и все свойства (флуктуировать) вокруг некоторых средних значений. В сущности каждая система, находясь в таком коллективе с постоянной общей энергией, находится в некотором термостате, так как определение общей энергии для данного числа тел эквивалентно заданию температуры.
Таким образом, рассматривая средние свойства системы в ансамбле и колебания этих свойств, мы в сущности изучаем средние свойства и флуктуации (отклонения) их при заданной температуре.
Пусть общее число систем в ансамбле равно М. Распределение систем по состояниям задается совокупностью чисел M указывающих число систем в состоянии i. Каждое распределение может быть осуществлено определенным числом способов. Очевидно, что, как и в статистике молекул Больцмана и в этом случае должно иметь место наиболее вероятное распределение, осуществляемое наибольшим числом способов. Чтобы найти это распределение, необходимо определить максимум числа способов (ω) осуществления распределения. Системы в отличие от молекул различимы, и поэтому способы осуществления распределения определяются числом перестановок систем:
ω = M!/
Mi!.
Надо искать максимум ω при дополнительных условиях:
∑Mi = M и ∑MiEi = Ea.
Применив формулу Стирлинга, получим:
Sa = k ln ω = k[M ln M - ∑Mi ln Mi]
(XI. 14)
где Sa - энтропия ансамбля.
Воспользовавшись методом Лагранжа, как это сделано в гл. XI, § 2, найдем для наиболее вероятного распределения систем по состояниям
Mi = M(e-βEi/∑e-βEi)
(XI.15)
и из уравнений (XIII.64) и (XIII.65)
Sa = k[M ln М - ∑Mi (ln М - βEi - ln ∑e-βEi)]
или
Sa = k(βEa + M ln ∑e-βEi),
292
где
Ea = ∑MiEi.
Из соотношения dS/dE = 1/T следует, что β = 1/kT. Таким образом:
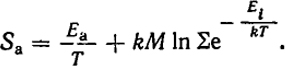
Средние значения энергии и энтропии системы определяются соотношениями Е =
и
S =
, т.е.
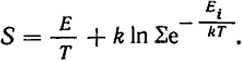(XI.16)
Мы видим, что величина энтропии системы определяется как величина
Q = ∑e-
,
(XI.17)
носящая название суммы состояний системы.
Здесь сумма берется по всем состояниям (а не энергиям) системы.
Статистика Гиббса может быть применена и к идеальному газу. Роль систем при этом будут играть молекулы и согласно уравнению (XI.15). Числа молекул в состоянии i(Ni) определится уравнением
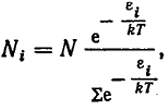(XI.18)
где N - общее число молекул, εi - энергия молекул в состоянии i
293
