§ 5. Закон распределения энергии по степеням свободы

Для многоатомного газа наряду с вопросом о распределении молекул по координатам и импульсам возникает вопрос о распределении по углам, характеризующим вращение, и внутренним координатам, характеризующим колебания. В частности, возникает важный вопрос, определяющий физический смысл температурного равновесия. Как распределяется энергия молекул по различным степеням свободы при заданной температуре?

287

Для решения этой задачи следует определить, как энергии вращения и колебания зависят от координат и импульсов. При вращении расстояния между атомами не меняются, поэтому энергия вращения E_вр целиком кинетическая. Пусть масса т вращается на расстоянии r от некоторой оси, тогда

ε_вр = mυ,

но

υ = ωr,

где ω - угловая скорость, следовательно:

p_вр = mω²r²/2.

Импульс вращения р_вр определяется общим соотношением

p_вр = ∂ε_вр/∂q = ∂ε_вр/∂ω

или

p_вр = mωr².

Если вращается несколько тел с разными массами на различных расстояниях от оси, но с одинаковой угловой скоростью, то

ε_вр = (ω²/2)∑mr².

Как известно, величина I, определяемая уравнением

I = ∑mr²,

носит название момента инерции.

Соответственно

p_вр = ωI

и

ε_вр = p²_вр/2I.

Положение оси двухатомной молекулы, как и всякой линии в пространстве, определяется двумя углами. Следовательно, кинетическая энергия вращения двухатомной молекулы будет содержать два члена:

ε_вр = (p

2

1

  2I₁) + (p

2

2

  /2I₁).

Положение жесткой многоатомной молекулы в пространстве определяется тремя углами. Поэтому

ε_вр = (p

2

1

  2I₁) + (p

2

2

  2I₂) + (p

2

3

  2I₃).

Мы не останавливаемся на вопросе о том, как рационально выбрать эти углы.

288

Таким образом, энергия вращения выражается квадратично через импульсы и для многоатомной молекулы имеет три квадратичных члена.

Колеблющаяся частица имеет как кинетическую E_к = p

2

кол

  /2m, так и потенциальную энергию.

Для гармонического колебания потенциальная энергия выражается квадратично через отклонение q. Действительно, поскольку возвращающая сила f пропорциональна отклонению:

f = -γq,

где γ - упругая постоянная, то

ε_пот =

q

∫

0

  γq²/2.

Следовательно, энергия гармонического колебания характеризуется двумя квадратичными членами:

Рассчитаем, сколько независимых колебаний может совершать r-атомная молекула.

Всего r-атомная молекула имеет 3 r степеней свободы. Из них шесть относятся к поступательному и вращательному движениям. Таким образом, для r-атомной молекулы при r > 2 число колебаний равно 3r - 6, число квадратичных членов в колебательной энергии равно 6 r - 12, а общее число всех квадратичных членов в выражении энергии

6r - 12 + 6 = 6r - 6.

Рассчитаем среднюю энергию молекулы, приходящуюся на один квадратичный член, и докажем, что она равна kT/2 независимо от вида энергии.

Для конкретности рассмотрим среднюю энергию ε_i, приходящуюся на квадратичный член:

ε_i = β_iq

2

i

  ,

где β_i - некоторая постоянная.

По определению среднего значения

Согласно уравнению (XI.5), число молекул, имеющих

289

заданное значение q_i:

Таким образом:

Умножая числитель и знаменатель на Δq_i и переходя к пределу, получим

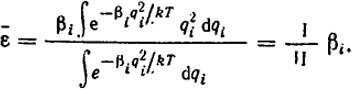
С интегралом П, стоящим в знаменателе, мы уже встречались, а интеграл I может быть получен дифференцированием интеграла П по β_i/kT.

Таким образом:

II = √πkT/β_i; I = 1/2√π(kT)³/β

3

i

 

и

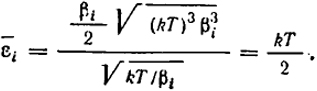(XI.12)

Закон, иногда называемый неточно законом равномерного распределения энергии по степеням свободы, следует называть законом равномерного распределения энергии по квадратичным членам:

Средняя энергия одного колебания (kT) вдвое больше средней энергии одного вращения (kT/2), так как колебанию отвечают два квадратичных члена, а вращению - один. Средняя кинетическая энергия одинакова для любой степени свободы. Этот вывод представляется естественным. Трудно было бы представить, чтобы молекулы газа, например, не вращались. Между различными видами движения непрерывно происходит обмен энергией при ударах молекул. Невращающиеся молекулы могут приобрести вращательное движение после столкновения.

Закон распределения энергии по степеням свободы разъясняет смысл температурного равновесия. Для того, чтобы газ имел температуру Т, все резервуары энергии (квадратичные члены) должны быть заполнены. Запас кинетической энергии поступательного движения у всех

290

газов одинаков и для одного моля составляет (3kT/2) N_A = 3RT/2.

Одним из следствий закона распределения энергии по степеням свободы является закон Авогадро-Жерара, согласно которому в одинаковых объемах газа при одинаковых давлении и температуре содержится одинаковое число молекул.

Известно, что давление возникает в результате изменения импульсов молекул при ударе их о стенки сосуда.

Расчет приводит к формуле:

pV = 1/3Nmu², (XI.13)

где u² - средний квадрат скорости.

Величина mu² = 2ε_кин одинакова у всех газов при одинаковой температуре. Из формулы (XI. 13) непосредственно видно, что если два газа находятся при одинаковых р, V и Т, то они содержат одинаковое число молекул N.

291