§ 2. Вывод закона распределения Больцмана

Задача установления распределения молекул идеального газа по областям фазового пространства сводится к рассмотрению числа способов (ω_i) распределения N_i молекул, находящихся в i-той области фазового пространства, по g ячейкам. Примем, что априорная вероятность попадания в любую ячейку фазового пространства не зависит от того,

278

к каким значениям координат и импульсов она относится. Это положение представляет выражение одной из аксиом квантовой механики, утверждающей одинаковую априорную вероятность каждого квантового состояния.

Напомним, что в качестве осей фазового пространства взяты импульсы, а не скорости и что соотношение (XI.2), являющееся одним из выражений аксиоматики квантовой механики, формулируется для импульсов, а не для скоростей.

Если бы мы в фазовом пространстве в качестве осей взяли скорости, а не импульсы, одинаковым объемам отвечала бы разная априорная вероятность.

Так как каждому способу осуществления распределения молекул в одной области соответствуют все способы распределения молекул в других областях, то общее число способов равно произведению чисел способов размещения молекул в каждой области, т.е. ω = Пω_i.

Определение ω_i особенно просто для случая высоких температур. Очевидно, что чем выше температура, тем большей энергией обладают молекулы, тем больше их проникает в фазовые области, соответствующие высокой энергии. Следовательно, с повышением температуры плотность расселения молекул в фазовом пространстве уменьшается и при достаточно высокой температуре N_i ≪ g.

Это означает, что практически в каждой ячейке будет одна или не будет ни одной молекулы. Поэтому для случая высоких температур можно не учитывать принцип Паули, ограничивающий число частиц в одной ячейке. Этот принцип будет рассмотрен в гл. XXI.

Для определения ω_i будем последовательно размещать N_i молекул по g ячейкам области. Очевидно, что каждую молекулу можно разместить, g способами, помещая в одну из ячеек. Отсюда следует, что общее число размещений равно g^N_i. Однако нужно учесть, что при таком расчете мы считаем молекулы отличными.

Действительно, мы считаем те размещения, при которых молекулы меняются местами. Другими словами, поскольку в каждой ячейке не более одной молекулы, то мы, учитывая их перестановки, каждое размещение считали N_i! раз. Таким образом:

ω_i = g^N_i!N_i!

и

ω =

П

i

 ω_i = g^N/

П

i

  N_i!,

279

где N = ∑N_i - общее число молекул.

Для того, чтобы найти равновесное (наиболее вероятное) распределение, следует искать максимум ω при учете постоянства числа молекул N и общей энергии Е системы¹:

N = ∑N_i и Е = ∑е_iN_i,

где ∑ берется по всем областям; ε_i - энергия молекулы в i-той области. Вместо максимума ω можно искать максимум энтропии S, которая монотонно растет с увеличением ω согласно уравнению

S = klnω.

Стоящая перед нами задача решается путем нахождения относительного экстремума. Отыскиваются значения N_i, отвечающие максимуму величины

S = kln(g^N/

П

i

  N_i!)

при дополнительных условиях: ∑N_i - N = 0
∑ε_iN_i - E = 0.

Функция N_i! - прерывная, имеющая смысл лишь при целых значениях переменных. Для больших значений N_i можно воспользоваться формулой Стирлинга:

nN_i! - N_ilnN_i - N_i.

Таким образом:

Для решения задачи относительного максимума следует умножить дополнительные условия на постоянные (А и В) и сложить полученные произведения с функцией, экстремум которой определяется. Это приведет к выражению,

k{Nlng - ∑N_ilnN_i + N} + A{∑N_i - N} + B(∑N_iε_i - E).

Продифференцировав это выражение по N_i и приравняв результат нулю, получим

-k(1 + lnN_i) + A + Bε_i = 0.

Отсюда

lnN_i = A₁ - B₁ε_i

280

и

N_i = A₂e^-B₁ε_i

где A₁, A₂ и B₁ - постоянные.

Для определения постоянных А₂ и B₁ можно использовать дополнительные условия. Мы осуществим это лишь в отношении A₂:

∑N_i = N = A₂

∑e

обл

  ^-B₁ε_i

откуда

A₂ = N/

∑e

обл

  ^-B₁ε_i

Таким образом:

Число молекул, попадающих в фазовую область, отвечающую энергии ε_i, должно зависеть от температуры. Поэтому и величина B₁ должна зависеть от температуры.

Мы могли бы ввести температуру с помощью второго дополнительного условия, связав энергию газа с температурой.

Однако рациональнее воспользоваться термодинамическим соотношением (см. гл. II)

dS = δq/T.

Из уравнений (XI.3) и (XI.4) следует:

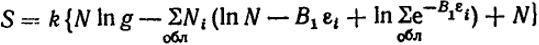
или

Если объем системы постоянен, то

δqdE

и

dS = dE/T.

Из уравнения (XI.5) следует, что

dS/dE = B₁k = 1/T,

откуда

B₁ = 1/kTю

Таким образом, мы получаем один из важнейших законов

281

статистики - закон распределения Больцмана:

Величина N_i равна числу молекул в фазовой области, т.е. числу молекул, обладающих координатами и импульсами вблизи некоторых заданных значений.

Обычно представляет интерес менее детальная характеристика - число молекул N_qj или N_pj. обладающих заданным (в некотором интервале) значением одной координаты (q_j) или импульса (q_i).

Покажем, что внешний вид формулы (XI.6) сохраняется применительно к этим задачам.

Если нас интересует число молекул (N_qj), имеющих координату q_j в интервале от q_j до q_j + Δq_j независимо от значений остальных координат и импульсов, то мы должны просуммировать выражение (XI.6) по всем импульсам и другим координатам (кроме q_j):

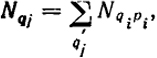
где q_J - все координаты q_i, кроме q_j.

Такая запись индексов суммирования обозначает, что суммирование ведется по всем импульсам (p_i) и всем координатам (q_i), кроме q_j. Поскольку N_qipi = N_i, то

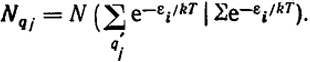
Обычно энергия выражается как сумма слагаемых, зависящих от отдельных координат или импульсов. Выделим слагаемое, зависящее от q_j

ε = ε(q_i) + ε(q

’

j

  ),

тогда

N_qj = N∑e-[ε(q_i) + ε(q

’

j

  )]/kT ∣ ∑e_-εi/kT.

Так как рассматриваемая сумма произведений равна произведению сумм, то

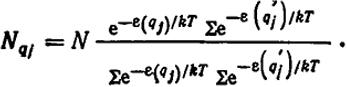
282

Следовательно:

Умножив числитель и знаменатель на Δq_j и рассмотрев предельное значение знаменателя, получим

Аналогично можно получить, что

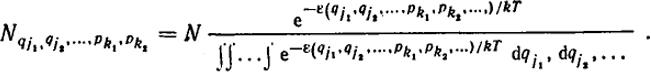
Мы рассмотрим три наиболее важных примера применения закона Больцмана.

283