Часть втораяСТАТИСТИЧЕСКАЯ МЕХАНИКА
Термодинамика позволила создать рациональный метод расчета равновесий. Однако формальность построения термодинамики ограничивает область ее применения. Термодинамика не может описать скорости процессов. Предсказания положений равновесия в термодинамике носят абсолютный характер. Между тем из приведенной в гл. II статистической трактовки энтропии ясно, что состояния с меньшими значениями энтропии возможны, хотя и менее вероятны. Эти отклонения от равновесных состояния (флуктуации) также не описываются термодинамикой. Наконец, в рамках термодинамики не вскрывается механизм процессов, связь между макроскопическими свойствами тел (термические и калорические коэффициенты) и микроскопическими характеристиками молекул.
Полное описание тепловых явлений может быть сделано лишь на основе рассмотрения тел как совокупности молекул. Молекулы подчиняются законам механики, однако благодаря их огромному числу необходимо применение методов статистики.
Статистическая механика - это механика больших коллективов. В статистической механике нет никаких аксиом, кроме аксиом механики и положений теории вероятности. Естественно, что термодинамика должна войти в статистическую механику как часть. Аксиомы и понятия термодинамики получают обоснование в статистической механике.
Изучение статистической механики целесообразно начать с проблемы распределения, включающей вопросы равновесия.
С молекулярной точки зрения равновесие следует описывать как распределение молекул между различными состояниями. Так, в системе жидкость - пар молекулы распределяются между жидкой и паровой фазами. При химическом равновесии, выражаемом каким-либо химическим уравнением, молекулы могут быть в двух состояниях, отвечающих
273
двум частям этого уравнения, следовательно, они распределяются между этими состояниями.
Распределение может относиться не только к макроскопическим, но и микроскопическим характеристикам. Так, представляет интерес распределение молекул по скоростям. Для решения ряда задач важно знать распределение двухатомных молекул по величинам углов, образованных их осями с направлением поля.
Полная запись распределения заключается в детальной характеристике всех молекул как механических систем. У одноатомной молекулы имеются шесть таких характеристик. Это ее координаты х, у, z и составляющие ее импульса px, py, pz. У r-атомной молекулы таких характеристик 6r, так как каждый атом имеет те же шесть характеристик.
Таким образом, r-атомная молекула характеризуется 3r-координатами и 3r-импульсами. В качестве координат qi нецелесообразно выбирать координаты атомов. Эти координаты выбираются таким образом, чтобы в них была возможность описывать поступательное, вращательное и колебательное движение молекул. Поступательное движение описывается изменением координат центра тяжести молекул, вращательное - углами между осями молекул и осями координат, колебательное - изменением расстояний между атомами.
По законам теоретической механики импульс рi - определяется как производная кинетической энергии по соответствующей скорости qi т.е. pi = ∂Eкин/∂qi.
Графически состояние молекул можно изобразить в виде точек в так называемом фазовом пространстве. Осями такого пространства выбираются координаты и импульсы молекулы. Для молекулы одноатомного газа, таким образом, фазовое пространство имеет шесть осей, для r-атомного газа 6r осей. При этом каждая молекула опишется отображающей ее точкой в фазовом пространстве, а ее движению в обычном пространстве будет отвечать некоторая линия в фазовом пространстве.
Рассмотрим в качестве примера колебание точки вдоль оси х. Фазовое пространство в этом случае будет плоскостью с осями х и рх. При гармоническом колебании х = Аsin 2πνt; px = m(dx/dt) = 2πmνAcos2πνt, где А - амплитуда; ν - частота колебаний.
Исключив t из этих двух уравнений, получаем
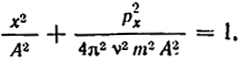 (IX.1)
(IX.1)
274
Таким образом, фазовая линия будет представлена эллипсом, по которому движется отображающая точка.
Полное механическое описание моля одноатомного газа требует задания 6NA чисел (NA - число Авогадро), а r-атомного 6NA r чисел.
Однако такое описание слишком детально. Нет необходимости задавать точно механические характеристики молекулы; их можно задавать с некоторой неточностью (ΔxΔyΔzΔpxΔpyΔpz), зависящей от характера задачи. Это значит, что и положение отображающей точки в фазовом пространстве будет определено неточно. Утверждается лишь, что она находится в некоторой области фазового пространства.
Следовательно, распределение должно описать, сколько молекул (точнее - отображающих точек) находится в различных областях фазового пространства. Размер (объем) области, равный ΔxΔyΔzΔpxΔpyΔpz, остается неопределенным, так как в зависимости от требований задачи допускается различная точность в задании координат и импульсов. Мы можем разделить фазовое пространство на области одинакового объема. Распределение опишется совокупностью чисел Ni, указывающих число молекул в каждой области.
Мы ввели в разделе термодинамики (гл. II) понятие термодинамической вероятности, определяющей число способов создания определенного состояния. Одно из состояний, отвечающее наибольшей вероятности, будет равновесным, а остальные, менее вероятные, могут возникнуть как флуктуации. Примем, что априорная вероятность попадания молекулы во все области одинакова. Позднее мы вернемся к обоснованию этого положения.
Рассмотрим распределение для случая идеального газа. Отсутствие взаимодействия молекул упрощает задачу, так как вероятность попадания молекулы в какую-нибудь область не зависит от числа других молекул, находившихся в этой области.
Расчет числа способов осуществления различных распределений относится к задачам комбинаторики, часто встречающимся в теории вероятности. На рис. XI.1 изображен ящик, на дне которого имеются перегородки, ограничивающие области.
Поместим некоторое количество шариков в ящик. После встряхивания произойдет распределение шариков по областям. Это распределение также может быть описано совокупностью чисел Ni. Каково число способов осуществления
275
такого распределения? Различные способы определяются тем, что совокупность чисел Ni можно осуществить, меняя места различных шариков. Каким же числом способов да можно распределить N молекул по группам, содержащим N1, N2, ..., Ni молекул? Известно, что общее число перестановок, которое можно выполнить из N предметов, равно N!. Однако искомая величина ω будет меньше, чем
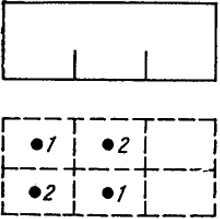
Рис. XI.1. Схема размещения шаров по секциям

Рис. XI.2. Схема размещения шаров по ячейкам секций
N!. Действительно, перестановки молекул внутри групп не дают нового распределения, которое может возникнуть только при перемещении молекул из одной группы в другую. Таким образом, величина N\ содержит лишние перестановки. Легко подсчитать число лишних перестановок. Например, внутри первой группы оно равно N!. Так как с каждой лишней перестановкой сочетаются перестановки всех остальных молекул, то, например, введение двух лишних перестановок удваивает общее число перестановок. Следовательно, для определения w необходимо общее число перестановок (N!) разделить на числа всех перестановок в каждой из групп. Таким образом:
ω =
.
В качестве примера под схемой ящика на рис. XI.1 показаны два способа осуществления распределения: N1 = 1, N2 = 1, N3 = 0.
Три верхние, ограниченные пунктиром, области соответствуют первому распределению, а три нижние - второму. При первом распределении в первой области находится
276
шарик 1 во второй - шарик 2. При втором распределении шарики поменялись местами.
Однако для вычисления величины вероятности (ω) различных распределений молекул такая комбинаторика непригодна. Дело в том, что в случае шариков осуществляются различные распределения за счет обмена шариков. Следовательно, мы отличаем шарики друг от друга.
Надо ли молекулы тоже считать различными? Очевидно, от этого зависит величина ω, а следовательно, и S, которая непосредственно связана с ω (гл. II). Желательно, чтобы энтропия, определенная статистическим методом, совпала с этой функцией, фигурирующей в термодинамике.
Не раз подчеркивалось, что энтропия обладает аддитивностью. Это свойство будет утеряно, если мы будем различать отдельные молекулы. Действительно, представим себе два объема одного и того же газа, разделенные перегородкой. Удалим перегородку. Если молекулы отличимы, то энтропия должна возрасти, как это происходит при перемешивании разных газов [см. уравнение (V.28)].
Таким образом, аддитивность энтропии требует последовательного проведения концепции неотличимости молекул. Но, возможно, при дальнейшем развитии физики удастся различать какие-либо группы молекул. Действительно, научились, например, различать молекулы, включающие различные изотопы одного элемента, которые ранее считались неразличимыми.
Как неоднократно указывал В.И. Ленин, всякое утверждение, передавая черты действительности, упрощает ее, отсекая лишь эти черты. В этом смысл неразличимости молекул. Если нас в рамках рассматриваемой задачи не интересует изменение изотопного состава, то мы должны "отсечь" факт существования изотопов и считать молекулы с разными изотопами неотличимыми. По мере развития познания мы будем все больше различать молекулы, сохраняя неотличимость для более узкого их круга.
Отказ от отличимости молекул, на первый взгляд, лишает нас базы для расчета числа способов осуществления состояния. Действительно, если шарики неотличимы (например, очень быстро меняются местами), то все расположения в примере с ящиком можно осуществить лишь одним способом.
Основания для комбинаторики мы находим не в различимости молекул, а в различимости отдельных участков фазовой области. Представим себе, что области в ящике, о котором шла речь выше, разделены на участки (на рис.
277
XI.2 показано разделение каждой области на два участка).
Тогда возможны различные способы распределения за счет перестановок частиц по участкам. Под рисунком схематично показано, что распределение N1 = 1, N2 = l, N3 = 0 может быть осуществлено четырьмя способами.
Что же играет роль участков фазовой области? Мы здесь сталкиваемся еще раз с квантовой теорией, которую привлекали для объяснения физического смысла третьего закона термодинамики (гл. IV). Тогда фиксировалось внимание на формулировке квантовой теории, утверждающей дискретность энергетических уравнений. Непосредственно с этой формулировкой связана другая, утверждающая дискретность фазового пространства. Согласно этой формулировке, одновременно координата q и составляющая импульса по этой координате рq могут быть указаны лишь с некоторой неточностью (δq, δpq). При этом
δqδpq = h,
(IX.2)
где h - постоянная Планка, 6,62·10-34 Дж·с.
Итак, точное указание положения отображающей точки в фазовом пространстве невозможно. Может быть лишь указана ячейка фазового пространства, в которой находится точка. Размер ячейки в отличие от размера области строго определен. Для одномерного движения одноатомной молекулы площадь ячейки равна h, а для трехмерного h3 так как δxδyδzδpxδpyδpz = h3.
Установление этого размера означает не ограничение точности описания, вызванное целесообразностью применительно к данной задаче, а важнейшую новую характеристику свойств частицы. Если мы описываем микрочастицу языком координат и импульсов, мы должны ввести дискретность фазового пространства. Очевидно, что область по размеру должна быть больше ячейки.
Так как мы делим фазовое пространство на равные области, мы можем принять, что каждая область состоит из g ячеек. Величина g неопределенна, как и размер области.
278
