В предыдущих разделах этой главы были рассмотрены вопросы термодинамики гальванических элементов и электродных процессов. Было показано, что источником электрической энергии гальванического элемента является химичсская реакция, энергия Гиббса которой определяет величину э. д. с. Так, например, э. д. с. элемента Якоби (рис. IX.3) определяется работой, выигрываемой при переносе
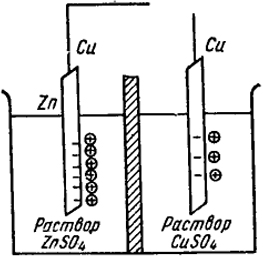
Рис. IX.3. Медно-цинковый гальванический элемент Б.С. Якоби

Рис. IX.4. К понятию о контактной разности потенциалов
245
электрона от медного проводника, присоединенного к цинковому электроду, к медному проводнику, находящемуся в контакте с медным электродом.
Поскольку работа электрических сил не зависит от пути процесса, то ее величина останется такой же, если вместо непосредственного перехода электрона осуществляется переход по другому пути.
Очевидно, что внутри проводников не может быть разностей электрического потенциала. Скачки потенциала возникают только на границах фаз. Поэтому э. д. с. элемента представляет собой алгебраическую сумму скачков потенциала φ. Так, для рассматриваемого случая
E = φCu/Zn + φZn/ZnSO4 + φZnSO4/CuSO4 + φCuSO4/Cu.
(IX.24)
В этом уравнении величина φCu/Zn означает скачок потенциала на границе двух металлов.
Таким образом, измеряемая э. д. с. этого элемента, равная приблизительно 1,1 В, распределяется между четырьмя указанными скачками потенциала. Заметим, что величина э. д. с. элемента не зависит от материала проволоки, которая его замыкает. Это следует из закона Вольта, согласно которому э. д. с. цепи, состоящей только из металлических проводников, равна скачку потенциала между первым и последним проводниками.
Действительно, если бы элемент был замкнут, например, железной проволокой, то вместо одного скачка потенциала между металлами φCu/Zn в цепи было бы два таких скачка φCu/Fe + φFe/Zn. однако эта сумма согласно закону Вольта, для цепи Cu—Fe—Zn равна скачку потенциала между медью и цинком, т.е. φCu/Zn = φCu/Fe + φFe/Zn.
В течение более ста лет в электрохимии не было достигнуто однозначного решения вопроса о том, где локализована э. д. с., т.е. какими скачками потенциала она в основном определяется. Существовали две концепции. Согласно физической теории, выдвинутой впервые А. Вольта, величина Е определяется исключительно скачком потенциала на границе двух металлов, а нальчшо растворов придавалось лишь подчиненное значение.
Химическая теория, развивавшаяся В. Нернстом, исходила из того опытного факта, что возникновение электрического тока в гальванических элементах связано с протеканием химических реакций, дающих необходимую для их работы энергию. Поэтому В. Нернст считал, что э. д. с. полностью определяется суммой скачков потенциала на границах металл - раствор. Однако при этом в химической теории совершенно обходился вопрос о скачке потенциала на границе между металлами, который в действительности существует.
Величина скачка потенциала на границе двух металлов, например φCu/Zn, обусловлена разницей в работе выхода электрона из разных металлов. Работа выхода у цинка меньше, чем у меди, и поэтому при
246
соприкосновении металлов цинк зарядится положительно, а медь - отрицательно. Следует, однако, ясно представлять, что величина скачка потенциала φ на границах фаз не может быть измерена. При переносе электрона из одной фазы в другую совершается не только электрическая работа, но и работа, обусловленная разницей его химических потенциалов, которые неодинаковы в разных фазах. Если бы мы располагали электрическим зарядом, не связанным с частицей, то работа переноса действительно определяла бы скачок потенциала между фазами.
Практически мы можем измерять скачок потенциала между двумя точками в одной фазе, так как при этом не изменяется химический потенциал. Таким образом, в уравнение (IX.24) введены величины φ, не поддающиеся измерению. Ранее мы вводили также не поддающиеся измерению термодинамические характеристики отдельных ионов. Ряд физиков (В. Гейзенберг, Э. Гуггенгейм и др.), разделяя идеалистические воззрения эмпириокритицизма, утверждают, что физик может оперировать лишь величинами, которые, по крайней мере, в принципе могут быть измерены. Эта концепция неправильна.
В соответствии с ленинской теорией познания эмпирические и рациональные элементы познания должны сочетаться друг с другом. В конечном счете, понятия, вводимые не на основе непосредственного опыта, а интуитивно, опираются на практику человеческой деятельности. Очевидно, что так называемые "принципиально неизмеримые" величины не могут быть определены лишь с помощью современной физики. Боязнь научной интуиции и "отрыва" от непосредственного опыта, как показывает история, неоднократно задерживала развитие науки. Так, В. Оствальд возражал против молекулярной теории, поскольку ее основные понятия в то время были интуитивными и не были подкреплены экспериментами.
Как отмечалось, скачки потенциалов на границах фаз не могут быть измерены. Гак называемая контактная или вольтова разность потенциалов представляет собой разность потенциалов в вакууме в двух точках, находящихся вблизи поверхностей двух разных металлов. Различие контактной разности потенциалов е от скачка потенциала φ на границе двух металлов поясняется рис. IX.4.
Переводя электрон двумя путями из точки I в точку II, получим
εZn/Cu = φвакуум/Zn + φZn/Cu + φCu/вакуум
(IX.25)
или
εZn/Cu = φZn/Cu + (φCu/вакуум - φZn/вакуум).
(IX.26)
Скачки потенциалов на границе металл - вакуум φCu/вакуум и φZn/вакуум редь частичным выходом электронного облака за пределы кристаллической решетки металла. Отдельно слагаемые правой части уравнения (IX.25) не могут быть измерены. Различные методы измерения ведут лишь к определению е. Поскольку эта величина играет большую роль в современной электровакуумной технике, то были разработаны
247
надежные методы ее определения. Эти методы могут быть разбиты на три группы. Один из методов, называемый ионизационным, заключается в следующем.
Пусть пластинки из меди и цинка помещены в вакууме на некотором расстоянии друг от друга и соединены вольтметром с очень большим сопротивлением. Вследствие контактной разницы потенциалов между пластинками возникает электрическое поле. Если теперь подвергнуть пространство между пластинками облучению каким-либо источником радиоактивного излучения (α- или β-излучателем), то произойдет ионизация, и газовые ионы будут двигаться к пластинкам и разряжаться на них в соответствии со своим знаком.
Для восстановления зарядов на границах металл - вакуум через внешнюю цепь должен проходить ток, по силе которого можно вычислить контактный потенциал. Попутно можно заметить, что такое устройство по существу представляет собой один из типов приборов для превращения атомной энергии в электрическую.
В так называемых конденсаторных методах меняется расстояние между двумя соединенными друг с другом металлическими пластинками, помещенными в вакуум. Так как емкость конденсатора зависит от расстояния между его обкладками, то при перемещении пластинок должен меняться заряд, т.е. будет протекать ток. Величина контактной разности потенциалов определяется по значению компенсирующей внешней э. д. с. Третья группа методов основана на том, что контактная разность потенциалов равна разности работ выхода электронов из двух металлов.
Вернемся к рассмотрению рис. IХ.4. Работа переноса электрона из точки I в точку II W = εZn/Cu. Перенесем теперь электрон из точки I в точку II по пути, указанному стрелкой. При переходе электрона из вакуума в цинк выигрывается работа выхода электрона WZn. Переход электрона из цинка в медь не связан с выигрышем и скачок потенциала компенсирован разницей энергий Гиббса электронов в двух металлах. Учитывая, что при переходе электрона из меди в точку II (в вакууме) затрачивается работа выхода WCu, получим
εZn/Cu = WZn - WCu.
(IX.27)
Величины работы выхода электрона могут быть определены на основе изучения фотоэлектрических и термоэлектрических явлений, и по уравнению (IX.25) может быть определена контактная разность потенциалов, которая является
248
единственным измеряемым скачком потенциала, обусловленным разницей в природе металлов.
Экспериментальные определения показали приблизительное соответствие между рядом величин разностей контактных потенциалов и рядом напряжений. Это привело к заключению о том, что э. д. с. гальванических элементов по своей величине и природе близки к контактным потенциалам. С этой точки зрения гальванический элемент подобен описанному выше элементу, используемому в ионизационном методе определения контактной разности потенциалов. Однако такое утверждение противоречит опытным фактам, показывающим, что э. д. с. элементов зависит от концентрации ионов в растворе, от степени окисления ионов и, наконец, от природы растворителя, в то время как контактная разность потенциалов зависит лишь от природы металлов.
Согласно точке зрения В. Нернста, э. д. с. обусловливается двойными электрическими слоями, возникающими на границах металл - раствор вследствие перехода ионов.
Для решения проблемы Вольта, т.е. вопроса о соотношении между контактными потенциалами и э. д. с. гальванических элементов, акад. А.Н. Фрумкин поставил задачу выяснения роли двойных слоев в создании э. д. с. Очевидно, если выбрать такие концентрации электролитов, при которых не будет перехода ионов металла в раствор или в обратном направлении, то э. д. с. должна быть близка к контактной разности потенциалов. Такая концентрация электролита, при которой на электроде отсутствует заряд, обусловленный переходом ионов, носит название нулевой концентрации. Потенциал электрода, находящегося в растворе такой концентрации, называется нулевой точкой данного металла или потенциалом нулевого заряда. Существование контактной разности потенциалов вовсе не означает неправильность уравнения (IX.7), полученного из представлений, развивавшихся Нернстом. Контактный, потенциал лишь входит как составляющая в величину Е в этом уравнении.
Каким образом могут быть определены нулевая концентрация и потенциал нулевого заряда? А.Н. Фрумкин предложил два метода решения этой задачи.
Первый может быть понят из рассмотрения следующего опыта. Мелкораздробленный порошок металлического серебра помещается в раствор, содержащий AgNO3 (при концентрации с) и избыток соли, например KNO3. Пусть концентрация AgNO3 в нулевой точке равна c0. Если концентрация
249
AgNO3 в растворе больше этой величины, т.е. c < c0, то ионы Ag+ будут осаждаться на порошке, который зарядится положительно. При этом ионы Ag+ притянут эквивалентное количество ионов NO
так, что благодаря большой поверхности порошка концентрация AgNO
3 в растворе заметно уменьшится.
Если же с < с0, то серебро будет переходить в раствор в виде ионов Ag+, и порошок зарядится отрицательно.
При избытке в растворе KNO3 ионы серебра будут обмениваться на ионы K+ и концентрация AgNO3 в растворе увеличится. Очевидно, при с = c0 концентрация AgNO3 в растворе не изменится. Таким образом, может быть найдена нулевая точка. Этот метод, однако, связан со значительными трудностями, обусловленными необходимостью определения малых изменений концентраций. В настоящее время они могут быть существенно уменьшены путем применения радиоактивных индикаторов.
Второй метод определения нулевой точки основан на том, что наличие заряда на поверхности вследствие взаимного отталкивания одноименных зарядов приводит к уменьшению поверхностного натяжения. Он применяется в случае электродов из жидких металлов, например ртути, галлия, амальгам, а также и для более тугоплавких металлов с использованием в качестве электролита расплавленных солей.
В случае легкоплавких металлов (ртути) для этой цели применяется простой прибор, изображенный на рис. IX.5, называемый капиллярным электрометром.
Мениск жидкого металла, например ртути, находящийся в коническом капилляре А и соприкасающийся с раствором, является исследуемым электродом. Ртуть не выливается из вертикальной трубки вследствие действия сил поверхностного натяжения. Поверхностное натяжение ртути и, следовательно, высота мениска в капилляре, отмечаемая микроскопом М, зависят от скачка потенциала на поверхности металл - раствор.
Пусть, например, металл заряжен положительно по отношению к раствору. Одноименные заряды, находящиеся на поверхности ртути, отталкиваются друг от друга и действуют против сил поверхностного натяжения. Таким образом, чем больше будет заряд поверхности, тем меньше должно быть поверхностное натяжение ртути. Величина поверхностного натяжения а измеряется высотой столба ртути и, необходимой для удержания мениска на определенном
250
уровне, и может быть вычислена по известной формуле: σ = hdgr/2;
где d - плотность ртути; g - ускорение силы тяжести; r - радиус мениска.
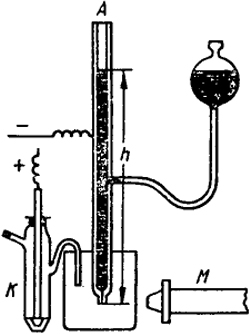
Рис. IX.5. Капиллярный электрометр
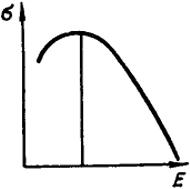
Рис. IX.6. Электрокапиллярная кривая
Величина потенциала на границе металл - раствор относительно какого-либо электрода сравнения K, например каломельного, измеряется потенциометром, с помощью которого можно накладывать разности потенциала между ртутным мениском и электродом сравнения. При этом потенциал K остается неизменным, а между электродами проходит ток, доводящий потенциал ртути до желаемой величины.
Допустим, что на ртуть, имевшую положительный по отношению к раствору заряд, при помощи потенциометра накладывается отрицательный потенциал. Очевидно, при этом ее заряд будет уменьшаться, а поверхностное натяжение возрастет. Такое увеличение σ будет продолжаться до тех пор, пока полностью не нейтрализуется положительный заряд ионов на поверхности ртути. Дальнейшее увеличение отрицательного заряда приведет к изменению знака двойного слоя, т.е. металл начнет заряжаться отрицательно по отношению к раствору, и изменится высота столбика ртути в капилляре. При этом вследствие отталкивания друг
251
от друга одноименных (отрицательных) зарядов поверхностное натяжение вновь уменьшается.
На рис. IX.6 представлена типичная кривая, показывающая зависимость поверхностного натяжения σ от потенциала ртути Е.
Уравнение этой кривой, называемой электрокапиллярной, выведенное Липманом и Гельмгольцем, имеет вид:
∂σ/∂E = -ε,
где ε - заряд единицы поверхности ртути; Е - потенциал.
Из этого уравнения следует, что в максимуме электрокапиллярной кривой величина ε = 0, т.е. поверхность ртути не заряжена. Согласно представлениям Нернста, при этом вообще отсутствует двойной слой и, следовательно, нулевые точки всех металлов должны совпадать, а скачок потенциала на границе металл - раствор равен нулю. Однако на самом деле в нулевой точке исключается лишь источник э. д. с., обусловленный переходом ионов из металла в раствор, и осуществляются условия выполнимости концепции Вольта.
Опыты А.Н. Фрумкина и его сотрудников показали, что потенциалы нулевых точек относительно стандартного водородного электрода для некоторых металлов имеют следующие значения:
| Металл . . |
Cd |
Zn |
Hg |
Ag |
Та |
| Е, В . . . |
-0,9 |
-0,63 |
-0,21 |
+0,05 |
+0,61 |
Измерения потенциалов нулевых точек позволили установить, что их разности для двух металлов действительно соответствуют контактной разности потенциалов (потенциалов Вольта). Следует, однако, отметить, что это утверждение не является совершенно точным, так как на границе металл - раствор может возникнуть скачок потенциала вследствие адсорбции и ориентации на поверхности металла нейтральных молекул. Такое явление может иметь место в случае, если молекулы характеризуются значительными дипольными моментами, например молекулы воды. Кроме того, на поверхности металла могут адсорбироваться и посторонние ионы.
Работы А.Н. Фрумкина и его школы позволили определить, в какой степени э. д. с. гальванических элементов обусловливаются контактной разностью потенциалов и в какой нернстовским двойным слоем. В обычных гальванических элементах оба источника э. д. с. имеют приблизительно одинаковое значение.
252
