Как указывалось, в бесконечно разбавленных водных растворах неэлектролитов коэффициент активности равен единице. Опыт показывает, что по мере увеличения концентрации электролита величины f уменьшаются, проходят через минимум, а затем снова увеличиваются и становятся существенно большими единицы в крепких растворах. Такой ход зависимости f от концентрации определяется двумя физическими явлениями.
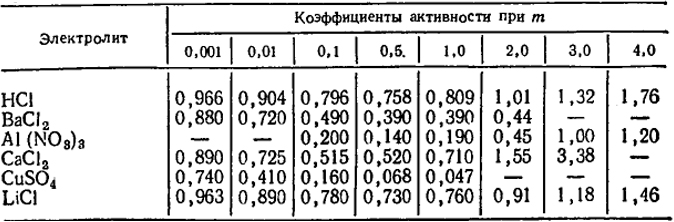
Первое особенно сильно проявляется при малых концентрациях и обусловлено электростатическим притяжением между противоположно заряженными ионами. Силы притяжения между ионами преобладают над силами отталкивания, т.е. в растворе устанавливается ближний порядок, при котором каждый ион окружен ионами противоположного знака. Следствием этого является усиление связи с раствором, что находит отражение в уменьшении коэффициента активности. Естественно, что взаимодействие между ионами возрастает при увеличении их зарядов. Так, например, для растворов одинаковой концентрации (m = 0,01) CuSO4, ВаСl2 и НСl величины f соответственно равны 0,41; 0,72 и 0,904. Значения коэффициентов активности некоторых электролитов в зависимости от моляльности приведены в табл. IX.1.
Таблица IX.1. Коэффициенты активности некоторых электролитов при различной моляльности
221
При возрастании концентрации все большее влияние на активность электролитов оказывает второе явление, которое обусловлено взаимодействием между ионами и молекулами воды (гидратацией). При этом в относительно концентрированных растворах количество воды становится недостаточным для всех ионов и начинается постепенная дегидратация, т.е. связь ионов с раствором уменьшается, следовательно, увеличиваются коэффициенты активности.
Известны некоторые закономерности, касающиеся коэффициентов активности. Так, для разбавленных растворов (приблизительно до m = 0,05) соблюдается соотношение 1 - f = k√m. В несколько более разбавленных растворах (т ≈ 0,01) величины f не зависят от природы ионов. Это обусловлено тем, что ионы находятся на таких расстояниях друг от друга, на которых взаимодействие определяется только их зарядами.
При более высоких концентрациях наряду с зарядом на величину активности начинает оказывать влияние и радиус ионов.
Для оценки зависимости коэффициентов активности от концентрации в растворах, где присутствует несколько электролитов, Г. Льюис и М. Рэндалл ввели понятие о ионной силе I, которая характеризует интенсивность электрического поля, действующего на ионы в растворе. Ионная сила определяется как полусумма членов, полученных умножением моляльностей каждого иона mi на квадрат его валентности Zi:
I = 1/2∑miZi.
(IX.18)
Было найдено, что в разбавленных растворах (т ≈ 0,01) коэффициент активности электролита является функцией ионной силы. Последняя определяется только концентрациями и валентностями присутствующих в растворе ионов, а не их природой. Например, ионная сила раствора KCl с моляльностью т равна т.
Так как любое измерение в соответствии с требованием электронейтральности дает результаты, относящиеся не к одному иону, а к их совокупности, то может быть определена лишь активность электролита, т.е. произведение активностей составляющих его ионов. Для вычисления активностей отдельных ионов необходимо сделать дополнительное допущение.
Г. Льюис, учитывал близость свойств ионов K+ и С1- (подвижность, ионный радиус, заряд и др.), принял, что
222
Таблица IХ.2. Зависимость коэффициентов активности ионов от ионной силы
| Валентность ионов |
Коэффициенты активности при ионной силе |
| 0,001 |
0.01 |
0,02 |
0,05 |
0,10 |
| 1 |
0,98 |
0,92 |
0,89 |
0,85 |
0,80 |
| 2 |
0,77 |
0,58 |
0,50 |
0,40 |
0,30 |
| 3 |
0,73 |
0,47 |
0,37 |
0,28 |
0,21 |
fK+ = fCl- Отсюда следует, что fK+ = fСl- = fKCl. Это допущение позволило рассчитать коэффициенты активности отдельных ионов. Например, зная fHCl можно найти коэффициент активности иона водорода по величине fHClHCl из соотношения fH+ = f
/
fCl-. Таким путем были получены величины, приведенные Б табл. IX.2.
В основе табл. IX.2, кроме допущения равенства коэффициентов активности ионов калия и хлора, лежит также предположение о том, что коэффициенты активности зависят только от ионной силы. Коэффициенты активности отдельных ионов, приведенные в табл. IX.2, зависят от сделанного предположения. Однако рассчитанные при ее помощи значения f для электролита не зависят от этого допущения.
В качестве примера вычислим, как изменится растворимость иодноватокислого бария в присутствии посторонних солей, например в 0,1-моляльном растворе KNO3. При 25°С в чистой воде растворимость Ва(IO3)2 составляет 8·10-4 моль в 1000 г воды. Для такого раствора I = 1/2(8·10-4·22 + 2·8·10-4) = 2,4·10-3.
Интерполируя данные табл. IX.2, находим f
= 0,72 и
fIO
= 0,96. Отсюда произведение активностей
L = 0,72×8·10
-4(0,96·2·8·10
-4)
2 = 1,36·10
-9. В случае, если раствор содержит KNO
3(
m = 0,1), величина
L останется неизменной, так как твердый Ва(IO
3)
2 сохранит свою активность. Однако величины
fBa2+ и
fIO
в присутствии KNO
3 уменьшатся и возрастет растворимость Ва(IO
3)
2. В этом случае ионная сила раствора равна 0,1 (пренебрегаем
I, обусловленной присутствием ионов Ва
2+ и IO
и, согласно табл. IX.2,
fBa2+ = 0,30 и
fIO
= 0,80. Отсюда можно найти
т из
L = l,36·10
-9 = (0,30
m) - (0,8·2
m)
2 и
m = l,21×10
-3 моль в 1000 г воды. Таким образом, растворимость
223
Ba(IO3)2 возросла примерно на 50 % вследствие добавления KNO3.
В заключение следует отметить, что в разбавленных растворах между коэффициентом активности иона, его зарядом и ионной силой было найдено эмпирическое соотношение
-lgfi = kZ
√I,
которое выводится в статистической теории электролитов.
224
