Как отмечалось выше, сильные электролиты в водных растворах практически полностью диссоциированы. Это утверждение основывается на многих опытных фактах. Существуют три области явлений (осмотические явления, ионные равновесия, электропроводность), изучение которых приводит к выводу о том, что поведение сильных электролитов не может быть описано классической теорией Аррениуса, справедливой лишь для слабых электролитов.
Осмотические явления. Степень диссоциации сильных электролитов в водных растворах определяли из результатов измерений точек замерзания и кипения, величин осмотического давления и давления пара растворителя. Оказалось, что значения а, полученные при помощи простых уравнений (например ΔT3 = iK3m), не совпадали друг с другом при использовании экспериментальных данных, полученных различными методами.
Ионные равновесия. Для сильных электролитов не соблюдается закон разведения Оствальда, уравнение (VIII.6).
Определения растворимости труднорастворимых солей также указывают на неприменимость закона действующих масс, если при выражении условий равновесия используют концентрации. Так, равновесие между твердым AgCl и его водным раствором согласно закону действующих масс должно описываться уравнениями:
AgCl
т ←
→ Ag
+ + Cl
- и
K =
cAg +
cCl,
где cAg+ и cCl- - концентрации ионов.
Поскольку AgCl является избыточной твердой фазой, концентрация этого вещества постоянна и входит в величину К. Как указывалось ранее, эта величина обозначается буквой L и носит название произведения растворимости.
213
Если произведение концентраций ионов серебра и хлора при данной температуре превышает величину L то из раствора должен выделяться осадок AgCl. По этой причине растворимость AgCl будет уменьшаться, если в растворе присутствуют другие соли, дающие ионы серебра или хлора (например, NaCl или AgNO3).
Опытные данные, однако, показывают, что этот вывод носит лишь качественный характер. В противоречии с законом действующих масс величина L не является постоянной и, в частности, зависит от концентрации посторонних солей, не дающих тех же ионов, что электролит, являющийся избыточной твердой фазой. Так, например, присутствие KNO3 существенно повышает растворимость AgCl. Характерно, что особенно сильно повышает растворимость подобных осадков (на 30-40 %) присутствие посторонних ионов с большими зарядами (например, А13+). Этот эффект не может быть объяснен в рамках классической теории.
Электропроводность. Как отмечалось выше, в случае слабых электролитов подвижность ионов не зависит от их концентрации, и поэтому соблюдаются соотношения α = λ/λ∞ и K = α2с/(1 - α), из которых следует, что при степени диссоциации, близкой к единице (т.е. при высоких< разведениях), разность 1 - α = 1 - λ.λ∞ должна быть пропорциональна концентрации. В действительности этот вывод теории оказывается несправедливым для растворов сильных электролитов, где наблюдается линейная зависимость между величинами 1 - λ/λ∞ и √c.
Совокупность перечисленных фактов, а также данные рентгеноструктурного анализа, показывающие, что сильные электролиты уже в твердом состоянии не содержат молекул, и их кристаллические решетки построены только из ионов, т.е. они полностью ионизированы, явились основанием для двух наиболее важных положений теории сильных электролитов.
Первое - степень диссоциации таких электролитов в растворах любых концентраций равна единице.
Второе - отклонения от идеальных законов обусловлены наличием взаимодействия между ионами. Иными словами, силы электростатического взаимодействия, которые удерживают ионы в кристаллической решетке, при растворении не исчезают, а лишь ослабляются. При этом следует иметь в виду, что кулоновские силы медленно убывают при увеличении расстояния между ионами. Вследствие электростатического притяжения каждый ион окружен множеством противоположно заряженных ионов.
214
Таким образом, растворы сильных электролитов даже при высоких разбавлениях представляют собой не идеальные, а реальные растворы, где каждый ион взаимодействует со всеми окружающими его ионами. В этом отношении такие растворы подобны твердым солям. Отличие заключается в том, что в первом случае имеет место лишь ближний порядок в расположении ионов, а во втором - дальний.
Сказанное позволяет понять отмечавшееся выше влияние посторонних солей на растворимость AgCl. Очевидно, чем выше валентность (заряд) иона, тем сильнее он взаимодействует с другими ионами в растворе, усиливает их связь с раствором и, следовательно, увеличивает растворимость других солей, не содержащих этого иона.
Существуют два пути построения теории сильных электролитов. Первый состоит в создании статистической теории, учитывающей электростатическое взаимодействие между ионами. Изложение такой теории приведено в гл. XIII. Второй путь, как и в теории растворов неэлектролитов,основан на введении функции активности, эмпирически описывающей термодинамическое поведение реальных растворов.
Недостатки второго пути сводятся к тому, что он не учитывает механизма явления, поэтому непосредственно не вскрывает причин отклонений в поведении реальных растворов от идеальности. Однако серьезное преимущество этого пути в точном описании явления, свободном от каких-либо допущений. Разумеется, эти два пути не являются взаимоисключающими, а должны дополнять друг друга. Целью теории термодинамической активности, как это уже отмечалось в гл. VI, является определение соотношений, позволяющих из результатов одного опыта предсказать результаты других. Такие соотношения содержат в себе учет отклонения от идеальности, поэтому могут быть использованы для предсказания тех или иных свойств, которые ранее определялись опытным путем.
Вычисление активности. Введение понятия активности для растворов электролитов имеет особенное значение, так как даже при малых концентрациях наблюдаются отклонения от идеальности. Как отмечалось выше, это обусловлено более медленным убыванием кулоновских сил с увеличением расстояния по сравнению с силами Ван-дер-Ваальса, характерными для межчастичного взаимодействия в растворах неэлектролитов.
Существует ряд методов, позволяющих определять активность
215
электролитов: изучение осмотических свойств, ионные равновесия и пр. Задача заключается в том, чтобы на Основании результатов измерений одним из этих методов получить данные об определенных свойствах растворов, которые могли бы использоваться для составления таблиц и давали бы возможность предсказать другие свойства растворов. Например, выбрав в качестве основы измерения температуру замерзания растворов и определив активность электролита, можно было бы найти все остальные свойства раствора - давление пара, температуру кипения и пр.
Для электролитов определение активности отличается тем, что активность компонента определяется его диссоциацией и образованием ионов. Например, диссоциация бинарного электролита, дающего одновалентные ионы K+ и А-, изображается уравнением KA = K+ + A-.
Обозначим активность такого электролита через a2, активность ионов через a+ и a-.
В соответствии с принятым в гл. VI стандартным состоянием для растворенных веществ (неэлектролитов) принимается, что активность ионов при бесконечном разбавлении должна совпадать с их моляльностью: a
=
m
и
a
=
m
.
Активность электролита при бесконечном разбавлении не может равняться моляльности, так как пропорциональна давлению пара, которое в свою очередь, для бинарных электролитов из-за диссоциации (см. закон Генри) пропорционально квадрату моляльности (концентрации). Поэтому стандартное состояние для бинарного электролита целесообразно выбрать так, чтобы при бесконечном разбавлении активность равнялась квадрату моляльности, a
= (
m2)
2.
Определим это стандартное состояние. Согласно уравнению (VI.2) a2 = p2/p
и для бесконечно разбавленного раствора
a
=
p
/
p
. Поскольку для рассматриваемого электролита
р
= г
2(
m
)
2, то
a
= г
2(
m
)
2/
рст. Учитывая, что
a
= (
m
)
2, найдем
p
= г
2.
Таким образом, выбор стандартного состояния совпадает с таковым для неэлектролитов. По закону действующих масс активность электролита и его ионов связана соотношением:
K =
a+a-/
a2.
(IX.9)
Численное значение K. зависит от выбора стандартного состояния. Для определения значения константы равновесия при принятом выше стандартном состоянии рассмотрим сно-
216
ва область бесконечного разбавления. Так как a
= (
m
)
2;
а
=
т
+;
а
=
т
и
т
=
m
=
, то
K = 1.
Таким образом, сделанный выбор стандартного состояния электролита эквивалентен установлению равенства /( = 1. Отсюда, согласно уравнению (IX.9)
а2 = а+а-.
(IX.10)
Коэффициент активности ионов следует выбирать так, чтобы его величина характеризовала в поведении ионов отклонения от идеальности и при достаточно больших разбавлениях была бы равна единице. Таким образом, для каждого из ионов, как и ранее для неэлектролитов
f+ = a+/m+
(IX.11)
f- = a-/m-
(IX.12)
Было бы неправильно, принять аналогичное определение для коэффициентов активности электролита, т.е. полагать, что f2 = а2/m2. Действительно, при бесконечном разбавлении a
= (
m
)
2 и
f
=
m
, т.е. коэффициент активности стремился бы не к единице, а к нулю. Поэтому коэффициент активности бинарного электролита определяется как
f2 = √a2/m2,
(IX.13)
откуда f
= 1 при бесконечном разбавлении.
При вычислениях часто используют понятие средней геометрической из активности двух ионов a±. Для одно-одновалентного электролита она определяется соотношением:
a± = (a+a-)1/2 = a
.
Подобным образом f± = (f+f-)1/2 = f
.
В общем случае, если электролит не бинарный и дает ν+ катионов и ν- анионов, т.е. γ = γ+ + γ-, то уравнение (IX.10) можно переписать в виде: a2 = a
+
a
. Соответственно изменится и написание последних уравнений. В частности, вместо уравнения (IX.13) получим соотношение:
 (IX.14)
(IX.14)
При разбавлении растворов сильных электролитов активность стремится не к концентрации, а определяется концентрацией в степени v. Например, для растворов ZnSO4
aZnSO4 = m+m- = m
,
217
а для растворов А12(SО4)3
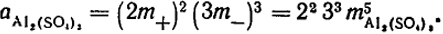
В качестве примера использования приведенных уравнений вычислим активность BaCl2 в растворе с m = 0,1 и и f2 = 0,5. Так, как в данном случае 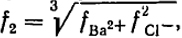 , то
, то 
218
