Важной характеристикой любого процесса является работа. Однако ее величина в одном и том же процессе в зависимости от способа его проведения может быть различной. Это обусловлено возможностью различных потерь работы, например вследствие трения. В результате фактически произведенная или затраченная работа не полностью характеризует процесс. Для того чтобы получить точное представление о данном процессе, вводят понятие о максимальной работе, которая могла бы быть произведена в идеальных условиях. Это возможно лишь в некотором воображаемом процессе, в ходе которого и система, и окружающая среда все время находятся в состоянии теплового равновесия. Подобный процесс является обратимым - все промежуточные состояния при переходе системы из начального состояния в конечное в точности повторяются на обратном пути, т.е. они по существу представляют собой последовательность бесконечно близких друг к другу положений равновесия. Если система, совершившая обратимый процесс, возвращается в исходное состояние также обратимым путем, то после этого ни в системе, ни в окружающей среде не остается каких-либо изменений. Реальные процессы могут лишь приближаться к обратимым, но для этого они должны совершаться бесконечно медленно.
Для дальнейшего изложения необходимо проанализировать процессы, протекающие при постоянной
температуре. Представим себе, что в этом случае газ заключен в вертикальном цилиндре с двигающимся в нем без трения поршнем. Пусть в начальном состоянии давление р1, а объем V1 (точка А на рис. I.3). Давление газа уравновешено насыпанным на поршень песком. Совокупность таких равновесных состояний описывается уравнением pV = const и изотермой 1 (см. рис. 1.3).
Если с поршня, находящегося в равновесии, снять относительно
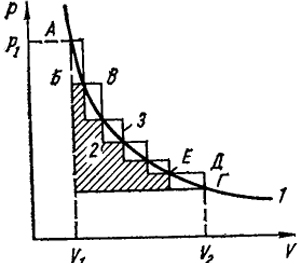
Рис. 1.3. К понятию об обратимом процессе
19
большое (конечное) количество песка, то поршень поднимается скачком, а давление резко уменьшится (до точки Б). При этом объем газа увеличится до значения, отвечающего новому состоянию равновесия (точка В), и будет произведена некоторая работа. При последовательном удалении конечных порций песка происходит дальнейшее расширение газа, который совершает работу за счет подводимого тепла от термостата, окружающего цилиндр. Характер такого процесса изображен (см. рис. 1.3) ступенчатой линией 2, а величина работы - заштрихованной площадью, лежащей под этой линией в пределах от начального объема V1 до конечного V2.
Если вновь сжимать газ, то под действием первой порции нагруженного песка давление резко возрастает (от точки Г до Д), затем объем газа уменьшится до равновесного (точка Е), При дальнейшем нагружении поршня может быть вновь достигнуто исходное состояние по ступенчатой линии 3. Из рис. I.3 видно, что затраченная на сжатие работа больше, чем полученная при расширении, и, следовательно, процесс проведен необратимо.
Вообразим теперь другой способ его осуществления, при котором груз с поршня снимается по одной песчинке, так что давление газа лишь на бесконечно малую величину превышает массу поршня и при столь малом расширении оно практически не уменьшается. При таком проведении процесса он приближается к обратимому и его протекание изображается кривой 1. Очевидно, процесс сжатия при нагружении поршня отдельными песчинками будет изображаться той же кривой (в обратной последовательности). Видно, что при таком обратимом расширении газа работа, совершенная им за счет подведенного тепла, больше, чем при любом необратимом расширении, т.е. максимальна. Очевидно также, что обратимые процессы всегда выгоднее необратимых.
Итак, обратимым называется такой процесс, направление которого на любой стадии может быть изменено на обратное, когда изменяется какой-либо параметр (в нашем случае давление) на бесконечно малую величину. Понятие обратимости - одно из наиболее важных в термодинамике. Мы вернемся к нему при рассмотрении ее второго закона. Пока же заметим, что в приведенном простом примере мы впервые сталкиваемся с вопросом о направлении физических процессов. Очевидно, что процесс, который может идти самопроизвольно в некотором определенном направлении, способен производить работу. Следовательно, такая
20
способность может быть сопоставлена с возможностью протекания процесса.
Рассмотрим теперь примеры применения первого закона термодинамики к процессам, протекающим при постоянных температуре, объеме и давлении, соответственно называющимися изотермическими, изохорическими и изобарическими. Найдем выражение для работы при обратимом проведении этих процессов.
Изотермический процесс. При расширении идеального газа dU = 0, поэтому, согласно уравнению (I.8), δQ = δW, т.е. все сообщенное газу тепло полностью превращается в работу. Величина работы определяется из уравнения (1.3). Так как для одного моля идеального газа р = RT/V, то
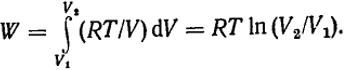 (I.9)
(I.9)
Изохорический процесс. При таком процессе δW = pdV = 0, так как V = const. Следовательно, по уравнению (I.8)
δQV = dU
(1.10)
или
QV = ΔU = U2 - U1.
(I.11)
Это означает, что при изохорическом процессе все тепло, подводимое к системе, идет только на увеличение ее внутренней энергии. Отсюда вытекает выражение для молярной теплоемкости при постоянном объеме CV. Согласно уравнению (1.10) и определению теплоемкости
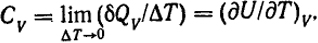 (1.12)
(1.12)
Сопоставляя уравнения (I.12) и (I.6), можно заметить, что теплоемкость при постоянном объеме характеризует возрастание внутренней энергии.
Для идеального газа (∂U/∂V)т = 0, и поэтому в выражении для CV можно заменить частную производную полной, т.е. CV = dU/dT.
Увеличение внутренней энергии тела при его нагревании от Т1 до Т2 определяется величиной интеграла:
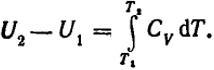 (I.13)
(I.13)
21
Для того чтобы найти численное значение интеграла, необходимо знать вид функциональной зависимости СV от Т. Здесь и дальше большая буква С обозначает теплоемкость одного моля вещества.
Изобарический процесс. Поскольку давление постоянно, то из уравнения (I.3) следует, что
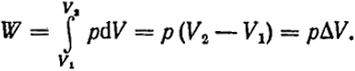 (1.14)
(1.14)
Условие p = const позволяет ввести давление под знак дифференциала в выражении работы δW = pdV в уравнении (I.8):
δQp = dU + d(pV) = d(U + pV).
(I.15)
Таким образом, тепло, придаваемое системе при постоянном давлении, расходуется на приращение некоторой функции H = U - pV, которая называется энтальпией или теплосодержанием. Энтальпия, как и внутренняя энергия, является функцией состояния. Ее изменение не зависит от пути процесса, так как изменения р и V определяются только начальным и конечным состояниями. Из уравнения (I.15) следует, что
δQp = dH;
(I.16)
Qp = ΔH = H2 - H1.
(I.17)
Из уравнений (I.10) и (I.16) видно, что в двух частных случаях (при постоянных объеме или давлении) количество тепла, сообщенное системе, равно изменению величин функции состояния U или Н. Иными словами, тепловые эффекты подобных процессов полностью определяются начальным и конечным состояниями системы. Обычно функция Н используется чаще, чем функция H, так как большинство реальных процессов протекает при постоянном давлении.
Изменение энтальпии характеризует количество тепла, сообщенного системе при изобарическом процессе. На этом основании можно определить теплоемкость при постоянном давлении уравнением
Cp =
(Qp/ΔT) = (∂H/∂T)p.
(I.18)
Уравнения (I.12) и (I.18) позволяют вычислить разность между молярными теплоемкостями при постоянных объеме и давлении для идеального газа. В этом случае величина CV может быть выражена через полную производную
22
U/dT. Величина H для идеального газа также не зависит от давления, а только от температуры, так как произведение pV при данной температуре постоянно. Таким образом, учитывая, что H = U + pV, находим
Cp =
=
=
+ R,
(I.19)
откуда следует, что
Cp - CV = R
(I.20)
т.е. теплоемкость одного моля идеального газа при постоянном давлении больше теплоемкости при постоянном объеме на величину, равную R, т.е. 8,314·Дж/(моль·К) или 1,987 кал/моль-К. Молярная теплоемкость одноатомных газов (благородные газы, пары некоторых металлов) при постоянном объеме равна 12,071·Дж/(моль·К). Из уравнения (I.20) следует, что для таких газов Сp = 12,071 + 8,314 = 20,385·Дж/(моль·К).
Из уравнения Клапейрона-Менделеева и выражения работы, как произведения pV, следует, что величина R есть работа расширения моля идеального газа при нагревании на 1К при постоянном давлении. Отсюда следует, что из уравнения (1.20) можно вычислить механический эквивалент тепла, приравняв разность теплоемкостей Ср и СV, выраженную в тепловых единицах, к работе расширения газа в механических единицах. Например, разность Ср - CV = R, выраженная в калориях, есть 1,987 кал/(моль·К), а в джоулях она равна 8,314. Отсюда калория эквивалентна 8,314/1,987 = 4,184 Дж. Подобный расчет впервые был сделан в 1842 г. одним из основателей первого закона термодинамики Р. Майером.
При нагревании твердых тел работа расширения незначительна по сравнению с изменением внутренней энергии. Поэтому Ср-CV для твердых тел меньше, чем для газов. Обычно она составляет 0,8÷1,2 Дж/(моль·К) и определяется не только работой, но и изменением внутренней энергии при изменении объема.
Напомним, что в случае адиабатического процесса, протекающего при полном отсутствии теплообмена между системой и окружающей средой, когда δQ = 0, согласно уравнению (I.8) δW = -dU. Так как dU = CVdT, то W = -
CVd
T. В случаях, когда
CV не зависит от температуры
W = CV(T1 - T2).
(I.21)
23
При рассмотрении термодинамических процессов принято считать работу положительной в том случае, если она производится системой; если же работа совершается внешними силами над системой, то она считается отрицательной. Например, при адиабатическом расширении газа работа совершается за счет уменьшения внутренней энергии, она в точности равна убыли этой функции и является положительной величиной. Как видно из уравнения (I.21), при адиабатическом расширении температура системы падает. При W > 0 T2 < T1, Очевидно, что при процессах адиабатического сжатия, когда W < 0 (работа совершается над системой), внутренняя энергия увеличивается и температура повышается.
24
