§ 5. Термодинамика диаграмм состояния

Диаграммы фазовых равновесий, подобные описанным выше, как правило, строят на основании экспериментальных данных, непосредственно характеризующих равновесие, например, по температурам и концентрациям компонентов при образовании той или иной фазы. Вместе с тем следует отдавать себе отчет в том, что диаграммы состояния отражают соотношения между термодинамическими свойствами всех фаз и компонентов, входящих в данную систему. Поэтому в принципе диаграммы состояния можно строить только на основе термодинамических расчетов. Для этого существует два пути.

Первый состоит в том, что находят уравнения зависимости энергии Гиббса от состава для всех фаз при данной температуре, а затем с учетом условий материального баланса между фазами ищут минимальное значение энергии Гиббса для всей системы. Число и состав фаз при минимуме G отвечает состоянию равновесия. Совместное решение системы полученных таким образом уравнений приводит к определениям температур и составов существующих фаз.

Второй альтернативный путь исходит из принципа использованного при выводе правила фаз, т.е. из утверждения о том, что при равновесии химические потенциалы каждого из всех компонентов во всех фазах равны друг другу. Для осуществления такого способа расчета диаграмм состояния необходимы данные для зависимости химических потенциалов μ_i всех компонентов во всех фазах от состава и температуры. Приравнивая затем величины для каждого компонента, получают систему уравнений, которую решают совместно с уравнениями материального баланса.

В настоящее время широко используют подобные способы расчетов для построения диаграмм состояний, трех и многокомпонентных систем с использованием современной вычислительной техники. Таким путем получают количественные характеристики равновесия в сложных многокомпонентных системах, необходимые для прогнозирования свойств новых сплавов.

Связь, существующая между диаграммами состояния и химическими потенциалами компонентов (или парциальными

187

энергиями Гиббса) в случае двойных систем может быть наглядно пояснена методами геометрической термодинамики.

В гл. V было показано, что касательная к кривой экстенсивное свойство - состав для бинарной системы отсекает на осях ординат отрезки, равные парциальным молярным величинам компонентов, например величины G_i (или μ_i). Это используется в геометрической термодинамике.

Рассмотрим сначала изменение энергии Гиббса механической смеси двух веществ А к В при некоторой постоянной температуре. Так как эти вещества не взаимодействуют друг с другом, то энергия Гиббса одного моля смеси G’ определяется просто по правилу смешения:

G’ = G_A(1 - x_B) + G_Bx_B = G_A + (G_B - G_A)x_B,

где G_A и G_B - молярные энергии Гиббса А и В, x_B - молярная доля В в смеси.

Из уравнения видно, что G’ линейно меняется при изменении состава смеси (прямая I на рис. VII.20). Допустим, что вещества А и В неограниченно растворимы друг в друге (например, в жидком состоянии). В этом случае энергия Гиббса раствора любой концентрации будет ниже, чем механической смеси, так как образование раствора есть самопроизвольный процесс и, следовательно, сопровождается убылью функции G.

Рис. VII.20. Зависимость энергии Гиббса от состава для механических смесей и раствора

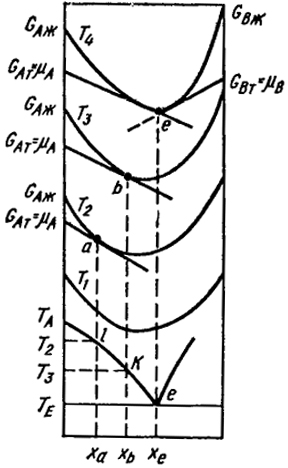
Рис. VII.21. Построение диаграммы состояния термодинамическим путем

188

Таким образом, зависимость G’ от состава для растворов, описываемая кривой II на рис. VII.20 должна лежать ниже прямой I. Эта кривая на всем протяжении от G_A до G_B является вогнутой. В противном случае отсутствовала бы неограниченная растворимость А и В. Действительно, существование выпуклого участка ab, который показан на кривой III (рис. VII.20), означало бы неустойчивость однородного раствора в пределах указанных концентраций.

Для доказательства проведем общую касательную к двум частям кривой III, проходящую через точки а и b. Теперь видно, что энергии Гиббса всех растворов на выпуклом участке кривой больше, чем механических смесей двух фаз, представляющих собой два раствора с концентрациями х_а и x_b. Следовательно, растворы, концентрации которых лежат между х_а и х_b не могут существовать при данной температуре и должны распадаться на две фазы, т.е. расслаиваться. Растворы, составы которых отвечают вогнутым участкам кривой G - х (G_A - а и G_B - b) термодинамически устойчивы (здесь отсутствуют другие фазы).

В трехкомпонентных системах для нахождения G_i или μ_i необходимо находить отрезки, отсекаемые на вертикальных осях плоскостями, касательными к трехмерным поверхностям, отражающим зависимость μ_i(G_i) от состава. Напомним, что при составах фаз, отвечающих точкам касания общей касательной, химические потенциалы каждого из компонентов в этих фазах равны между собой. Следовательно, можно графически определить составы существующих фаз, путем построения общих касательных к кривым зависимостей G’ - x_i.

Покажем это на примере диаграммы состояния первого типа для случая кристаллизации чистого компонента А из расплава А - В. В нижней части рис. VII.21 показана часть диаграммы двухкомпонентной системы, а в верхней - кривые зависимости энергии Гиббса моля расплава при различных температурах.

Согласно изложенному выше, в случае неограниченной растворимости в жидком состоянии кривые G - состав для всех расплавов должны быть вогнутыми к оси абсцисс. Энергия Гиббса всех тел с ростом температуры уменьшается, так как согласно уравнению (II.34) (∂G/∂T)_p = -S, а энтропия всегда положительна. Поэтому чем выше температура, тем ниже располагаются кривые G - состав. Кривая, соответствующая высокой температуре Т, лежащей выше точек плавления компонентов А и В, расположена

189

в нижней части графика. Все точки этой кривой соответствуют энергиям Гиббса меньшим, чем энергии Гиббса веществ А и В в твердом состоянии G_AT и G_BT. Поэтому невозможна кристаллизация А и В.

При более низкой температуре Т₂, лежащей ниже точки плавления чистого вещества А, соответствующая кривая лежит выше предыдущей. При этой температуре, как видно из рис. VII.21, молярная энергия Гиббса чистого → A в твердом состоянии ниже, чем в жидком. Иными словами, при этой температуре компонент A в жидком, состоянии неустойчив относительно твердой фазы и должен кристаллизоваться. При еще более низкой температуре Т₃, кривая G - x_i выше двух предыдущих и точка касания b соответствует точке k на линии ликвидус и молярной доле x_B. Проведение касательной к кривой G - состав при этой температуре позволяет найти точку k на линии ликвидус и состав расплава х_B. Наконец, при еще более низкой температуре T₄, соответствующей образованию эвтектики Т_Е, из расплава одновременно кристаллизуются компоненты А и В. Набор подобных кривых позволяет построить всю диаграмму состояния. Поясним, что при температуре ниже точки плавления компонента А величины G_Aж относятся к переохлажденной жидкости.

Рис. VII.22 поясняет описанный способ для построения диаграмм с ограниченной растворимостью в твердом состоянии. Кривая I относится к энергии Гиббса расплава при T₁, а кривая II - к твердому раствору α при T₁.

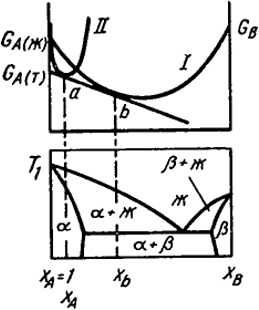
Рис. VII.22. Равновесие между расплавом и твердым раствором

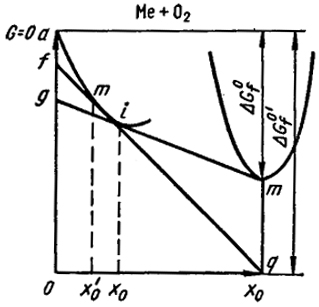
Рис. VII.23. Растворимость кислорода в твердом металле

190

Построение кривых G - состав полезно и для понимания равновесий с участием нестехиометрических соединений.

Рассмотрим диаграмму состояния системы, образованной твердым металлом и кислородом при постоянной температуре Т (рис. VII.23). Энергии Гиббса чистого металла (Me) и кислорода О₂ при p_O2 = 1, как обычно, принимают равными нулю (верхняя горизонтальная линия) а их изменения откладывают по вертикальной оси вниз. На нижней горизонтальной оси откладывается концентрация кислорода..

Пусть имеется измеримая растворимость кислорода в твердом металле. По этой причине энергия Гиббса раствора Me - O₂ уменьшается при увеличении концентрации последнего (кривая ai). При некоторой концентрации кислорода произойдет образование новой фазы - оксида Ме_хО_у. Эта концентрация определяется положением общей касательной к кривым ai и lmk, описывающей энергию образования оксида в области его гомогенности. Таким образом, искомая растворимость кислорода равна x_O. При некоторой другой температуре положение общей касательной может быть несколько другим и в этом случае раствор кислорода в металле, находился бы в равновесии с оксидом другого состава в гомогенной области.

Из рисунка VII.23 видно, что в случае оксида с более отрицательной энергией Гиббса образования ΔG

0

f

  растворимость кислорода в металле, определяемая положением общей касательной qmf, составит х

’

O

  . Она будет меньше, чем при равновесии с менее устойчивым оксидом.

191