Используемые в технике сплавы содержат больше двух компонентов. В состав большинства марок стали входят наряду с железом и углеродом так называемые легирующие элементы - Mn, Cr, Ni, Si и др. Несколько элементов обычно входит в состав сплавов на основе меди, олова, алюминия и многих других цветных металлов. Для описания фазовых равновесий в реальных сплавах во многих случаях достаточно знания диаграмм состояния для систем, состоящих из трех основных компонентов, например, для нержавеющих сталей из железа, хрома и никеля.
В трехкомпонентных сплавах при p = const, согласно уравнению (VII.2), максимальное число сосуществующих фаз составляет 4 (С = 0 = 3 + 1 - Φ). В области существования одной гомогенной фазы С = 3. Поэтому для построения
180
диаграммы состояния необходимы три оси координат, по которым можно было бы откладывать температуры и концентрации каких-либо двух из трех компонентов. Это, однако, неудобно из-за того, что концентрацию третьего компонента надо определять по разности. Чтобы избежать этого, используют прием, предложенный В. Гиббсом. Он заключается в том, что концентрации всех трех компонентов откладывают по сторонам равностороннего треугольника (рис. VII.14), который называют концентрационным

Рис. VII.14. Представление концентраций компонентов в тройной системе
Вершины треугольника соответствуют чистым веществам А, В и С, т.е. их стопроцентному содержанию или молярным долям, равным единице. Каждая из равных сторон треугольника представляет составы трех двухкомпонентных систем А - В, А - С и В - С. Эти стороны обычно делятся на 100 или 10 равных частей. Любая точка внутри треугольника отражает состав системы в массовых содержаниях, % (или молярных долях).
Существует два способа определения состава трехкомпонентной смеси, основанные на свойствах правильных треугольников. Первый определяется тем, что сумма перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, равна высоте ВН. Этот отрезок (высота) соответствует 100 % какого-либо компонента. Например, для точки Р (рис. VII.14) сумма перпендикуляров Ра + Pb + Pc = BH = 100 %. Отрезки Ра, Pb и Pc дают содержания А, В к С соответственно 20, 30 и 50 %.
Во втором способе за 100 % принимают сторону треугольника и наносят сетку линий, параллельных каждой стороне. Сумма отрезков таких линий, исходящих изданной
181
точки Р и кончающихся на сторонах треугольника (показаны стрелками) есть постоянная величина, равная любой из сторон. На рис. VII.14 эти линии показаны пунктиром. Для выбранной точки Р Pb’ + Pb’ + Рс’ = АВ - ВС = АС = 100 %. Путем переноса отрезков Ра’, Рb’, Рс’ параллельно самим себе на стороны АС и ВС находим, что смесь содержит 20 % А, 30 % В и 50 % С.
Следует обратить внимание на важные особенности линий внутри концентрационного треугольника. Линии, параллельные каждой из его сторон, представляют собой геометрические места точек для смесей с постоянным содержанием одного компонента. Например, на линии gf (рис. VII.14) постоянно содержание компонента В, равное 70 %. Линии, соединяющие вершины сторон треугольника с противоположными сторонами, являются геометрическими местами точек смесей, в которых остается постоянным отношение концентраций двух компонентов. Так, составы всех смесей вдоль прямой А характеризуются постоянным отношением концентраций В и С, а составы смесей, отвечающие точкам на высоте ВН, содержат компоненты А и С в постоянном отношении 1:1.
Очевидно, что диаграмма состояния трехкомпонентной системы не может быть представлена на плоскости даже при постоянном давлении, так как температура должна откладываться на координатной оси, перпендикулярной плоскости концентрационного треугольника.
На рис. VII.15 представлена простейшая объемная диаграмма состояния трехкомпонентной системы, в которой компоненты неограниченно растворимы друг в друге в жидком состоянии и совсем нерастворимы в твердом. Она является аналогом диаграммы двухкомпонентной системы первого типа. Графические изображения всех состояний системы находятся в призматическом пространстве. В его основании находится концентрационный треугольник, к сторонам которого перпендикулярны боковые плоскости. Каждая такая плоскость, по вертикальным координатам которой откладывается температура, представляет собой диаграмму состояния одной из трех двухкомпонентных систем. Три криволинейные поверхности Ае1Ee2, Ве1Ее3 и Се2Ee3 являются поверхностями ликвидус. Они представляют геометрические места точек, соответствующих составам и температурам, при которых из однородной жидкости (расплава) начинается кристаллизация чистых компонентов А, В к С соответственно. Пунктирные кривые е1Е, е2Е и е3Е образованы пересечением двух смежных поверхностей
182
и отражают изменения концентрации расплава, насыщенного одновременно двумя компонентами при изменении температуры. Например, кривая е1Е показывает изменение состава тройного расплава при равновесии с кристаллами А и В при изменении температуры, например,
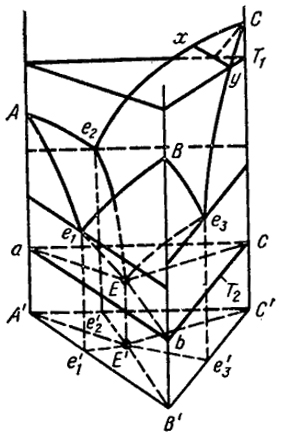
Рис. VII.15. Объемная диаграмма трехкомпонентной системы. Неограниченная растворимость в жилкой состоянии и отсутствие растворимости в твердом
при охлаждении. Эту кривую можно также рассматривать как описывающую понижение температуры кристаллизации двойной эвтектики А-В в зависимости от концентрации добавляемого третьего компонента С.
Три подобные друг другу кривые е1Е, е2Е и е3Е пересекаются в точке Е, соответствующей равновесию расплава с кристаллами А, В и С, Так как здесь существуют четыре фазы, то согласно уравнению (VII.2) число степеней свободы равно нулю (С = 3 - 4 + 1 = 0). В точке Е происходит кристаллизация тройной эвтектики, состоящей из компонентов А, В и С. При наблюдении структуры такой эвтектики под микроскопом видны относительно крупные кристаллы А, В и С и смесь мелких кристалликов этих же компонентов, образовавшаяся при затвердевании тройного эвтектического расплава, происходившего без изменения состава. Подобные тройные и четверные эвтектики таких металлов, как Pb, Bi, Sn, Cd, используют в качестве припоев и легкоплавких сплавов. Известный сплав Вуда, состоящий из упомянутых элементов плавится при 65° C и представляет собой четверную эвтектику.
183
Сечения объемной диаграммы горизонтальными плоскостями дают изотермические разрезы диаграмм тройных систем, т.е. отражают фазовые равновесия при одной постоянной температуре. Например, такое сечение диаграммы, представленной на рис. VII.15, при температуре Т показано на рис. VII.16 в виде треугольника ABC. Кривая
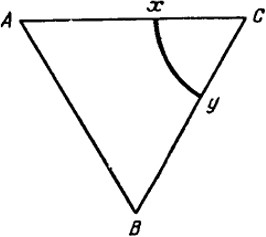
Рис. VII.16. Изотермическое сечение объемной диаграммы при
T1
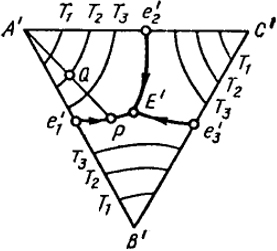
Рис. VII.17. Проекция объемной диаграммы на концентрационный треугольник
ху на этом рисунке есть сечение поверхности Се2Ее3 горизонтальной плоскостью. Криволинейный треугольник хуС ограничивает область двухфазного равновесия между расплавом и кристаллами С. Вне этого треугольника существуют лишь однородные расплавы. При более низких температурах (ниже точек A и В) из расплава начинается кристаллизация компонентов A и В, и на горизонтальных сечениях появляются двухфазные области, прилегающие к осям АА’ и ВВ’. Они подобны области хуС. По мере понижения температуры протяженность всех трех двухфазных областей увеличивается. Наконец, при температуре TE они смыкаются, образуя плоскость тройной эвтектики abc (рис. VII.15) или плоскость солидус. Ниже этой температуры жидкая фаза не существует.
Рассматриваемая пространственная диаграмма может быть представлена в виде диаграммы на плоскости, если использовать ее проекцию на концентрационный треугольник А’В’С’ (рис. VII.17). Линии е
Е’,
е
Е и
е
Е есть проекции линий кристаллизации двойных эвтектик
e1E,
е2Е и
е3Е (рис. VII.15), а области
А’е
Е’е
А,
В’е
Е’е
В’ и
С’е
Е’е
С’ - проекции поверхностей кристаллизации
184
компонентов А, В и С. Точка Е - проекция точки тройной эвтектики Е.
На рис. VII.17 представлена тройная диаграмма состояния на плоскости. Здесь на проекциях поверхностей кристаллизации компонентов (А1е1Ее2А1, B1eEe3B1, С1е2Ее3С1). нанесены изотермы, подобные ху (см. рис. VII.16) при разных температурах. С помощью этого рисунка можно проследить за превращениями при охлаждении (или нагревании) какого-либо сплава, например, при Т1, Т2 и Т3, когда Т1 > Т2 > Т3.
Пусть расплав, состав которого отвечает точке Q, охлажден до температуры Т2. Это означает, что при Т2 должна начаться кристаллизация компонента А. Как будет изменяться состав расплава при дальнейшем охлаждении? Так как из расплава выделяются только кристаллы А, то в оставшейся жидкости отношение концентраций В и С будет сохраняться постоянным. Как отмечалось выше, этому свойству отвечает ход прямых линий, соединяющих каждую вершину треугольника с противоположной стороной. В рассматриваемом случае это отрезок прямой A’Q. Следовательно, при дальнейшем охлаждении расплава, одновременно с накоплением кристаллов А, состав расплава будет изменяться в соответствии с прямой линией, являющейся продолжением A’Q. При достижении температуры, отвечающей точке Р, начнется выпадение двойной эвтектики А - В. При дальнейшем охлаждении расплав будет обогащаться компонентом С, а его состав изменяется по кривой РЕ до тех пор, пока при температуре точки Е вся жидкость не затвердеет с образованием тройной эвтектики.
Объемная диаграмма трехкомпонентной системы, в которой все три составляющие ее двойные системы характеризуются неограниченной растворимостью в твердом и жидком состоянии, представлена на рис. VII. 18. Она состоит всего из двух поверхностей. Верхняя поверхность - ликвидус - проходит по линиям ликвидус двойных систем и как бы накрывает их. Нижняя поверхность - солидус - также проходит по линиям солидус двойных систем и закрывает их снизу. По такой диаграмме для сплава любого состава, например определяемого точкой а, можно найти температуры начала и окончания его кристаллизации (или плавления) по точкам пересечения вертикали с плоскостями ликвидус и солидус (см. рис. VII.18).
Значительно сложнее диаграммы состояния трехкомпонентных систем, образующих химические соединения. Рассмотрим простейший случай, когда в системе образуется
185
лишь одно соединение АтВп, которое дает неограниченные растворы в жидком состоянии со всеми компонентами (А, В и С). Эти компоненты, в свою очередь, неограниченно растворимы друг в друге в жидком состоянии. Растворимость в твердом состоянии в системе практически отсутствует. Представим этот случай в виде диаграммы состояния
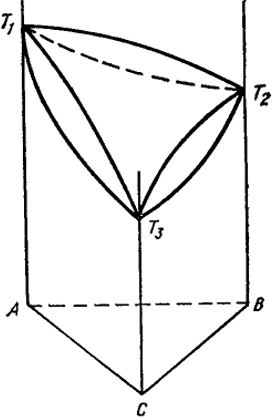
Рис. VII.18. Объемная диаграмма трехкомпонентнои системы: неограниченная растворимость в твердом и жидком состояниях

Рис. VII.19. Проекция диаграмм с двойным химическим соединением
на плоскости. На сторонах концентрационного треугольника (рис. VII.19) построены три двойные системы, которые на пространственной диаграмме были бы перпендикулярны к плоскости этого треугольника. Прямая линия аС соответствует сплавам, в которых отношение концентраций А и В постоянно и равно их отношению в химическом соединении (т:п). Таким образом, появляется еще одна двойная система АтВп - С, которую можно было бы изобразить вертикальным сечением с основанием на линии аС. Оно делит пространственную диаграмму данной системы на две такие же пространственные диаграммы, подобные представленной на рис. VII.15. Слева на ее вертикальных осях отложены температуры плавления А, С и АтВп, а справа АтВп, В и С. Кроме того, линия аС делит треугольник ABC на два неравные концентрационные треугольника АаС и аВС.
186
Точка е5 представляет проекцию двойной эвтектики АтВп - С на изотермическое сечение пространственной диаграммы при некоторой температуре Т. Точка Е2 отвечает тройной эвтектике, состоящей из эвтектик е2, е3 и е5.
187
