Рассмотрим изолированную систему, находящуюся в равновесии и состоящую из нескольких частей (фаз). Определим условия равновесия. Рассмотрим переход некоторой порции тепла δQV при постоянном объеме из какой-либо фазы в другую. Учитывая, что dS = δQV/T и в замкнутой системе при равновесии dS = 0, найдем соотношения между изменениями энтропии в двух частях системы:
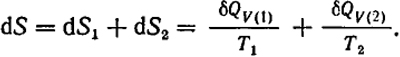
Поскольку при V = const δQV = dU и в замкнутой системе dU = dU1 + dU2, то δQV(1) = -δQV(2) и, следовательно, при равновесии T1 - T2.
Рассмотрим теперь процесс сжатия одной фазы вследствие расширения другой. Используя уравнение (II.15), найдем
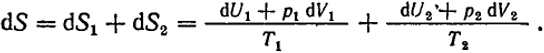
Так как по доказанному выше T1 = T2, dU1 = -dU2 и dV1 = -dV2, то p1 = p2.
Являются ли эти условия достаточными для характеристики равновесия? Очевидно, нет, так как может иметь место
160
переход вещества из одной фазы в другую. Как указывалось в гл. V, при постоянных р и Т условием равновесия при распределении компонента между двумя фазами является равенство его химических потенциалов в этих фазах.
Рассматривая подобным образом взаимодействие между любой парой фаз в сложной системе, можно прийти к выводу, что при равновесии все ее фазы имеют одни и те же температуру и давление (условия термического и механического равновесий). Кроме того, условия химического равновесия выражаются равенством величин μi для каждого компонента в каждой фазе.
Дадим определения понятий, используемых в правиле фаз.
Фазой (Φ) называется часть неоднородной системы, представляющая собой совокупность телесных объектов, имеющих определенный химический состав и термодинамические свойства, отделенная от других ее частей видимой поверхностью раздела. Более кратко можно определить фазу как однородную часть неоднородной системы, которая может быть извлечена из системы каким-либо механическим способом. Из этого определения следует, что в любой системе может быть только одна газовая фаза1. Естественно, что число твердых и жидких фаз в одной системе может быть больше единицы.
Числом компонентов (К) называется число индивидуальных веществ, входящих в систему, за вычетом числа независимых химических уравнений, связывающих эти вещества. Иными словами, число компонентов равно минимальному числу веществ, из которых может быть составлена система в данном состоянии. Поэтому К зависит от того какие процессы могут протекать в системе. При одном и том же числе индивидуальных веществ число компонентов может быть различным. Для примера рассмотрим смесь, состоящую из азота, кислорода и оксида азота NO. Здесь может быть три случая. Первый, когда температура настолько низка, что N2, O2 и NO химически не взаимодействуют между собой и, следовательно, число компонентов равно числу индивидуальных веществ, т.е. 3.
Обобщая, можно сказать, что в системах, где отсутствуют химические превращения, число компонентов равно числу индивидуальных веществ. Во втором случае, если
161
температура достаточно высока, происходит реакция N2г + O2г = 2NOг. При этом в состоянии равновесия между концентрациями трех газов существует связь, выражаемая одним уравнением Kp = p
/ (
pN2/
pO2). Отсюда следует, что K = 3 - 1 = 2.
В третьем случае также существует химическое равновесие, отличающееся тем, что исходная система состояла только из одного газа NO.
В силу этого возникает дополнительная связь между количествами трех газов. Она состоит в том, что при любых условиях концентрации кислорода и азота, образующихся из NO, всегда равны между собой. Отсюда K = 3 - 2 = 1. Здесь система, состоящая из трех веществ; имеет свойства однокомпонентной. Приведенное определение К позволяет уменьшить число параметров, характеризующих равновесие.
Числом степеней свободы (С) называется число независимых параметров (температура, давление и концентрации компонентов), задание которых полностью определяет состояние системы при равновесии. В этом состоянии параметры можно произвольно изменять в определенных пределах без изменения, числа и природы фаз. Например, в системе вода-пар от 0 до 100° C можно изменять температуру, не изменяя числа фаз (при этом давление пара будет меняться).
Найдем связь между Φ, К и С. Допустим, что все компоненты находятся во всех фазах, так как, в принципе, не существует полной нерастворимости. Подсчитаем общее число параметров системы (П). Для каждой фазы надо знать столько концентраций (с), сколько имеется компонентов. Поэтому для всех фаз число параметров, характеризующих концентрацию, равно КΦ. Учитывая температуру и давление как два общих для всей системы параметра, найдем, что П = K + 2. Однако не все эти параметры нет зависимы друг от друга. Важно, что концентрации компонентов в разных фазах связаны условиями равенства химических потенциалов, т.е. совокупностью уравнений: для 1,2,... k фаз:

162
где верхний индекс означает номер фазы, а нижний - компонента.
Каково число уравнений, связывающих все величины μi?
Так как величина μi какого-либо компонента в данной фазе равна его химическому потенциалу во всех остальных фазах, то для него число независимых уравнений составит (Φ - 1). Очевидно, для всех компонентов системы оно будет равно К(Φ - 1). Кроме того, для каждой фазы существует одно уравнение состояния, значит для системы число таких уравнений равно Φ.
Таким образом, общее число уравнений У, связывающих параметры, равно К(Φ - 1) + Φ. Разность между числом параметров П и числом связывающих их уравнений У, равна числу параметров, остающихся неопределенными. Эта разность и есть число степеней свободы, т.е. то число параметров, которое следует задать для однозначного определения состояния системы:
С = П - У = 2 + КΦ - К(Φ - 1) - Φ = К + 2 - Φ1.
(VII.1)
Уравнение (VII.1) является выражением правила фаз. Очевидно, число степеней свободы не может быть меньше нуля, поэтому из уравнения (VII.1) следует, что К+2 ≥ Ф, т.е. число фаз при равновесии не может превышать К + 2.
Возвращаясь к рассмотрению однокомпонентных систем, мы видим, что максимальное число фаз определяется условием С = 0 = 1 + 2Φ, т.е. равно трем.
При наличии двух фаз, например воды и пара С = 1 + +2-2 = 1.
Теперь можно также ответить на вопрос о максимальном числе фаз, которое может одновременно существовать в двух, трех и многокомпонентных системах. Так, для двухкомпонентных систем оно равно четырем (0 = 2 + 2 - Φ), для трехкомпонентных - пяти (0 = 3 + 2 - Φ) и т.д.
В большом числе практически важных случаев давление является постоянным. Это относится, например, к большинству металлургических процесов. Для таких случаев правило фаз выражается уравнением:
С = К + 1 - Φ.
(VII.2)
Рассмотрим, например, раствор углерода в жидком железе. Здесь в равновесии могут находиться (2 + 1 - Φ = 0)
163
три фазы, т.е. кроме расплавленного металла, могут быть еще две какие-либо фазы из трех возможных (графит, карбид железа, твердое железо).
Три оксида (CaO, A12O3, SiO2) образуют основу шлака в доменных печах. В этом случае максимальное число фаз составит 4.
Следует обратить внимание на особенность твердого состояния, заключающуюся в том, что чистое вещество может образовывать несколько кристаллических фаз, которые имеют одинаковый химический состав, но различаются по своим физическим свойствам. Например, существует пять различных фаз льда; белое и серое олово; α-, γ- и δ-железо и т.д.
Анализ этого явления, называемого полиморфизмом, облегчается при использовании правила фаз. Очевидно, превращение одной полиморфной фазы в другую (при постоянном давлении) может происходить только при одной строго определенной температуре, так как K = 1; Φ = 2 и С = 1 + 1 - 2 = 0.
Например, α-Fe (объемноцентрированная кубическая решетка) превращается в γ-Fe (гранецентрированная кубическая решетка) при 910 "С. Ниже этой температуры y-Fe находится в неустойчивом метастабильном состоянии. Выше 910° C неустойчиво α-Fe.
Правило фаз может быть применено для анализа систем, в которых имеет место химическое равновесие. Так, при обжиге известняка происходит реакция: СаСО3т = СаОт + СО2г. Если СаСО3 и СаО нерастворимы друг в друге, то Φ = 3. Число компонентов равно 2 и С = 2 + 2 - 3 = 1 . Это означает, что система имеет одну степень свободы, т.е., например, если задана температура, то давление углекислого газа при равновесии будет строго определенным. Это следует также из уравнения изобары (III.13), согласно которому Кр (в данном случае Kр = рCO2) является функцией температуры.
При восстановлении FeOт + COг = Feт + CO2г Φ = 3; K = 3; С = 3 + 2 - 3 = 2. Это означает, что из трех параметров состояния: температуры, общего давления р и состава газовой фазы произвольно можно выбрать лишь два. Если, например, задать Т и р, то концентрации газов будут однозначно определены в соответствии с условием Kp = pCO2/pCO2 Равновесные системы иногда классифицируют по числу степеней свободы. При С = 0 они называются нонвариантными, С = 1 - моновариантными, С = 2 - дивариантными и т.д.
164
1
И.Р. Кричевским было найдено, что при очень высоких давлениях в ряде газовых смесей (например, азота и аммиака) наблюдается расслоение компонентов без перехода их в жидкое состояние.
1
В общем случае число внешних параметров может быть и больше двух.
